2018_2019学年天津市和平区八下期末数学试卷

这是一份2018_2019学年天津市和平区八下期末数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 已知 △ABC 的三边分别是 6，8，10，则 △ABC 的面积是
A. 24B. 30C. 40D. 48

2. 若 xx−1 在实数范围内有意义，则 x 的取值范围是
A. x≥0B. x≥1C. x>1D. x≥0 且 x≠1

3. 化简 5n3n 的结果为
A. 3n5B. 5n23C. 5n3D. 5n3

4. 某市 6 月份日平均气温统计如图所示，则在日平均气温这组数据中，众数和中位数分别是
A. 21，21B. 21，21.5C. 21，22D. 22，22

5. 下列命题正确的是
A. 有一个角是直角的四边形是矩形B. 有三个角是直角的四边形是矩形
C. 对角线相等的四边形是矩形D. 对角线互相平分的四边形是矩形

6. 不论实数 k 取何值，一次函数 y=kx−3 的图象必过的点坐标为
A. 0,−3B. 0,3C. 32,0D. −32,0

7. 如图所示，菱形ABCD中，对角线AC、BD相交于点O，H为AD边的中点，菱形ABCD的周长为36，则OH的长等于
A. 4.5B. 5C. 6D. 9

8. 当 x=3 时，函数 y=x−k 和函数 y=kx+1 的函数值相等，则 k 的值为
A. 2B. 12C. −12D. −2

9. 关于函数 y=−2x+1，下列结论正确的是
A. 图象与直线 y=2x+1 平行B. y 随 x 的增大而增大
C. 图象经过第一、二、三象限D. 当 x>12 时，y<0

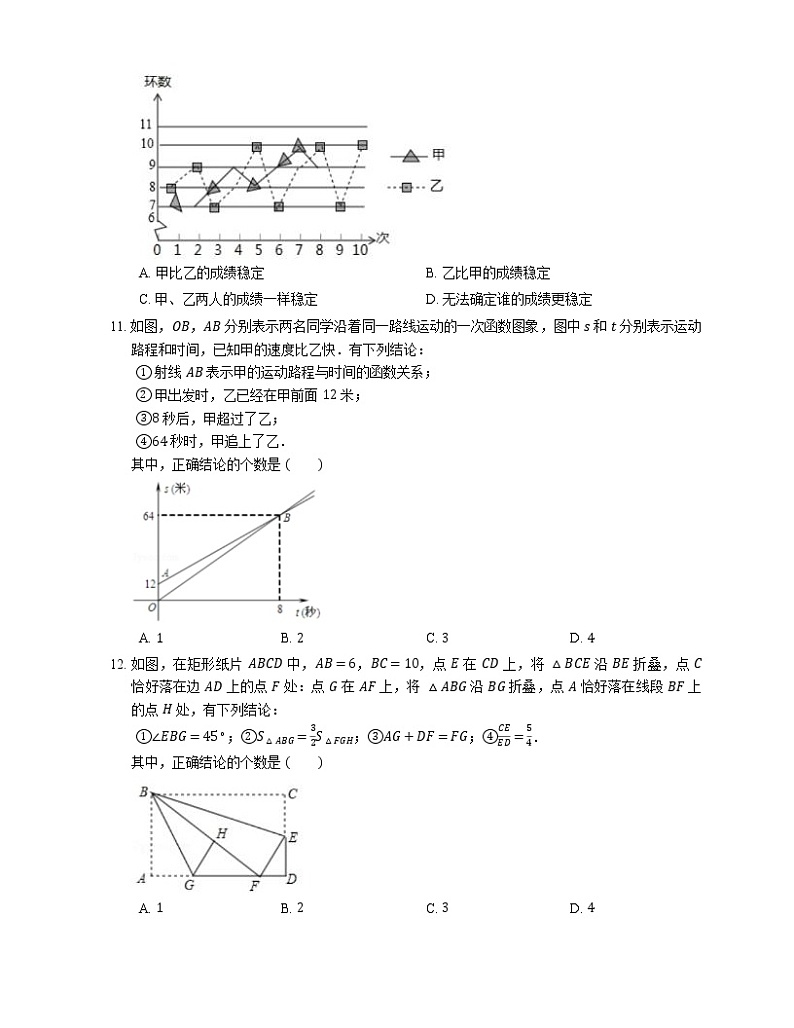
10. 如图是甲、乙两射击运动员的 10 次射击训练成绩的折线统计图，则下列说法正确的是
A. 甲比乙的成绩稳定B. 乙比甲的成绩稳定
C. 甲、乙两人的成绩一样稳定D. 无法确定谁的成绩更稳定

11. 如图，OB，AB 分别表示两名同学沿着同一路线运动的一次函数图象，图中 s 和 t 分别表示运动路程和时间，已知甲的速度比乙快．有下列结论：
① 射线 AB 表示甲的运动路程与时间的函数关系；
② 甲出发时，乙已经在甲前面 12 米；
③8 秒后，甲超过了乙；
④64 秒时，甲追上了乙．
其中，正确结论的个数是
A. 1B. 2C. 3D. 4

12. 如图，在矩形纸片 ABCD 中，AB=6，BC=10，点 E 在 CD 上，将 △BCE 沿 BE 折叠，点 C 恰好落在边 AD 上的点 F 处：点 G 在 AF 上，将 △ABG 沿 BG 折叠，点 A 恰好落在线段 BF 上的点 H 处，有下列结论：
①∠EBG=45∘；②S△ABG=32S△FGH；③AG+DF=FG；④CEED=54．
其中，正确结论的个数是
A. 1B. 2C. 3D. 4

二、填空题（共6小题；共30分）
13. 计算 5+35−3 的结果等于 ．

14. 某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：

如果公司认为，作为公关人员面试的成绩比笔试的成绩更重要，并分别赋予它们 6 和 4 的权，根据四人各自的平均成绩，公司将录取 ．

15. 已知一次函数 y=kx+2（k 是常数，k≠0），y 随 x 的增大而减小，写出一个符合条件的 k 的值为 ．

16. 如图，E，F，G，H 分别是正方形 ABCD 各边的中点，则四边形 EFGH 是 形．

17. 如图，正方形 OABC 的对角线 OB 在直线 y=−43x 上，点 A 在第一象限．若正方形 OABC 的面积是 50，则点 A 的坐标为 ．

18. 如图，在每个小正方形的边长为 1 的格中，点 C，D，E，F，G 均在格点上，DE 与 FG 相交于点 T．
（1）CD 的长等于 ；
（2）在如图所的网格中，用无刻度的直尺，画出：
① 以 DE 为一边的正方形；
② 以 CD，DT 为邻边的矩形 CDTP．

三、解答题（共7小题；共91分）
19. 计算：
（1）45+18−8−125；
（2）80+40÷5．

20. 某校为灾区开展了“献出我们的爱”赈灾捐款活动，九年级（1）班 50 名同学积极参加了这次赈灾捐款活动，
因不慎，表中数据有两处被墨水污染，已无法看清，但已知全班平均每人捐款 38 元．
（1）根据以上信息请帮助小明计算出被污染处的数据，并写出解答过程．
（2）该班捐款金额的众数，中位数分别是多少?
（3）如果用九年级（1）班捐款情况作为一个样本，请估计全校 1200 人中捐款在 40 元以上（包括 40 元）的人数是多少?

21. 如图，在三角形纸片 ABC 中，∠ACB=90∘，BC=5，AB=13，在 AC 上取一点 E，以 BE 为折痕，使 AB 的一部分与 BC 重合，点 A 与 BC 延长线上的点 D 重合．
（1）AC 的长 = ．
（2）求 CE 的长．

22. 在平行四边形 ABCD 中，
（1）如图 ①，若 AB=5，BC=3，则平行四边形 ABCD 的周长为 ；若 ∠A=70∘，则 ∠B 的度数是 ，∠C 的度数是 ；
（2）如图 ②，点 E 是平行四边形 ABCD 外一点，连接 DB 并延长交 CE 于点 F，且 CF=FE．求证 DF∥AE．

23. 某公司计划组织员工外出，甲、乙旅行社的服务质量相问，且对外报价都是 300 元/人，该公同联系时，甲旅行社表示可给每人八折优惠；乙旅行社表示可免去一人的费用，其余人九折优惠．
（1）根据题意，填写下表：
外出人数人1011甲旅行社收费元 2640乙旅行社收费元2430
（2）设该公司此次外出有 x 人，选择甲旅行社的费用为 y1 元，选择乙旅行社的费用为 y2 元，分别写出 y1，y2 关于 x 的函数关系式．
（3）该公司外出人数在什么范围内，选甲旅行社划算?

24. 已知，四边形 ABCD 是正方形，点 E 在边 AD 上，点 F 在边 AB 的延长线上，且 DE=BF，连接 EF．
（1）如图 ①，连接 CE，CF．求证：△CEF 是等腰直角三角形；
（2）如图 ②，BD 与 EF 交于点 M，若正方形 ABCD 的边长为 6，DE=2，求 AM 的长．
（3）点 G，点 H 分别在边 AB，边 CD 上，GH 与 EF 交于点 N，且 ∠GNF=45∘，若正方形 ABCD 的边长为 6，GH=35，求 DE 的长．（直接写出结果即可）

25. 在平面直角坐标系中，O 为原点，已知直线 y=12x+3 与 x 轴交于点 A，与 y 轴交于点 B，点 C 与点 A 关于 y 轴对称．
（1）点 A 的坐标为 ，点 B 的坐标为 ，点 C 的坐标为 ，直线 BC 的解析式为 ．
（2）点 M 是 x 轴上的一个动点（点 M 不与点 O 重合），过点 M 作 x 轴的垂线，交直线 AB 于点 P，交直线 BC 于点 Q．
① 如图 ①，当点 M 在 x 轴的正半轴上时，若 △PQB 的面积为 94，求点 M 的坐标；
② 连接 BM，若 ∠BMP=∠BAC，求点 P 的坐标．
答案
第一部分
1. A【解析】因为 62+82=102，所以 △ABC 是直角三角形，所以 △ABC 的面积 =12×6×8=24．
2. C【解析】∵xx−1 在实数范围内有意义，
∴x≥0，x−1>0，
解得：x>1，
则 x 的取值范围是：x>1．
3. D【解析】5n3n=5nn3n=5n3．
4. C【解析】这组数据中，21 出现了 10 次，出现次数最多，
∴ 众数为 21，
第 15 个数和第 16 个数都是 22，
∴ 中位数是 22．
5. B
【解析】A．有一个角是直角的平行四边形是矩形，故此选项不能判定是矩形；
B．有三个角是直角的四边形是矩形，能判定是矩形；
C．对角线相等的平行四边形是矩形，故此选项不能判定是矩形；
D．两条对角线互相平分四边形是平行四边形，故此选项不能判定是矩形．
6. A【解析】∵ 一次函数 y=kx−3，
∴ 不论 k 取何值，函数图象必过点 0,−3．
7. A【解析】【分析】可先求得AB的长，再根据三角形中位线定理可求得OH的长．
【解析】解：∵四边形ABCD为菱形，且周长为36，
∴AB=BC=CD=AD=9，
又∵O为BD中点，H为AD的中点，
∴OH为△ABD的中位线，
∴OH=12AB=4.5，
故选：A．
【点评】本题主要考查菱形的性质，掌握菱形的四边相等、对角线互相垂直平分是解题的关键．
8. B【解析】由题意：3−k=3k+1，
∴k=12．
9. D【解析】A．由于直线 y=−2x+1 与直线 y=2x+1 的 k 值不相等，
∴ 它们不平行，故本选项错误；
B．函数 y=−2x+1 中，k=−2<0，y 随 x 的增大而减小，故本选项错误；
C．函数 y=−2x+1 中，k=−2<0，b=1>0，此函数的图象经过一、二、四象限，故本选项错误；
D．函数 y=−2x+1 可化为 x=1−y2，依据 1−y2>12，可得 y<0，故本选项正确．
10. A
【解析】由图中知，甲的成绩为 7，7，8，9，8，9，10，9，9，9，
乙的成绩为 8，9，7，8，10，7，9，10，7，10，
x甲=7+7+8+9+8+9+10+9+9+9÷10=8.5，
x乙=8+9+7+8+10+7+9+10+7+10÷10=8.5，
甲的方差 S甲2=2×7−8.52+2×8−8.52+10−8.52+5×9−8.52÷10=0.85，
乙的方差 S乙2=3×7−8.52+2×8−8.52+2×9−8.52+3×10−8.52÷10=1.35，
∴S甲211. B【解析】∵ 射线 OB 所表示的速度为 648=8 米/秒，射线 AB 所表示的速度为 64−128=6.5 米/秒，而甲的速度比乙快，
∴ 射线 AB 表示乙的运动路程与时间的函数关系，
∴① 错误；
∵ 乙 8 秒走了 64−12=52 米，甲 8 秒走了 64 米，而他们 8 秒时相遇，
∴ 甲出发时，乙在甲前面 12 米，
∴② 正确；
∵ 甲乙 8 秒时相遇，而甲的速度比乙快，
∴8 秒后，甲超过了乙，
∴③ 正确；
④ 错误．
12. D【解析】∵△BCE 沿 BE 折叠，点 C 恰落在边 AD 上的点 F 处；
点 G 在 AF 上，将 △ABG 沿 BG 折叠，点 A 恰落在线段 BF 上的点 H 处，
∴∠CBE=∠FBE，∠ABG=∠FBG，BF=BC=10，BH=BA=6，AG=GH，
∴∠EBG=∠EBF+∠FBG=12∠CBF+12∠ABF=12∠ABC=45∘，
∴① 正确；
在 Rt△ABF 中，AF=BF2−AB2=102−62=8，
∴DF=AD−AF=10−8=2，
设 AG=x，则 GH=x，GF=8−x，HF=BF−BH=10−6=4，
在 Rt△GFH 中，
∵GH2+HF2=GF2，
∴x2+42=8−x2，解得 x=3，
∴GF=5，
∴AG+DF=FG=5，
∴③ 正确；
∵S△ABG=12×6×3=9，S△GHF=12×3×4=6，
∴S△ABG=32S△FGH，
∴② 正确．
设 CE=EF=x，在 Rt△EFD 中，x2=6−x2+22，
解得 x=103，
∴CE=103，DE=6−103=83，
∵CEDE=54，故 ④ 正确．
第二部分
13. 2
【解析】原式=52−32=5−3=2．
14. 乙
【解析】甲的平均成绩 =90×4+86×6÷10=876÷10=87.6（分），
乙的平均成绩 =83×4+92×6÷10=884÷10=88.4（分），
丙的平均成绩 =83×4+90×6÷10=872÷10=87.2（分），
丁的平均成绩 =92×4+83×6÷10=866÷10=86.6（分），
∵88.4>87.6>87.2>86.6，
∴ 乙的平均成绩最高，
∴ 公司将录取乙．
15. −1
【解析】∵ 一次函数 y 随 x 的增大而减小，
∴k<0，不妨设 k=−1．
16. 正方
【解析】连接 AC，BD，
∵E，F，G，H 分别是正方形 ABCD 各边的中点，
∴EH∥BD∥FG，EF∥AC∥HG，
EH=FG=12BD，EF=HG=12AC，
∴ 四边形 EFGH 为平行四边形，
∵ 四边形 ABCD 是正方形，
∴AC=BD，AC⊥BD，
∴EF=FG，EF⊥FG，
∴ 平行四边形 EFGH 是正方形．
17. 1,7
【解析】如图作 OF⊥OB，交 BA 的延长线于 F，作 BM⊥x轴 于 M，FN⊥x轴 于 N．
∵ 四边形 ABCD 是正方形，
∴∠OBA=45∘，
∵∠BOF=90∘，
∴△BOF 是等腰直角三角形，
∴OB=OF，
由 △BOM≌△OFN，可得 BM=ON，OM=FN，
∵ 正方形 OABC 的面积是 50，
∴OB=10，
∵ 点 B 在直线 y=−43 上，
∴B−6,8，F8,6，
∵BA=AF，
∴A1,7．
18. 26
【解析】（1）由勾股定理可得，CD=12+52=26．
（2）① 如图所示，四边形 CDEQ 即为所求．
② 如图所示，四边 CDTP 即为所求．
第三部分
19. （1） 原式=35+32−22+55=85+2.
（2） 原式=80÷5+40÷5=4+22.
20. （1） 被污染处的人数为：50−3−6−11−13−6=11（人），
被污染处的捐款数 50×38−10×3+15×6+30×11+50×13+60×6÷11=40，
答：被污染处的人数为 11 人，被污染处的捐款数为 40 元．
（2） 这组数据中 50 出现了 13 次，出现次数最多，则这组数据的众数是 50；
将组组数据从小到大依次排列，最中间的两数据是 40，40，
∴ 中位数为 40+40÷2=40．
（3） ∵ 九年级一班捐款数 40 元以上（包括 40 元）的有 30 人，占到 60%，
因此估计全校 1200 人捐款在 40 元以上（包括 40 元）的人数是 1200×60%=720，
答：全校 1200 人中捐款在 40 元以上（包括 40 元）的人数是 720 人．
21. （1） 12
【解析】∵∠ACB=90∘，BC=5，AB=13，
∴AC=12．
（2） 根据将其三角形纸片 ABC 对折后点 A 落在 BC 的延长线上，
则 AB=BD=13，
∵S△ABC=S△BCE+S△BDE，
∴12×5×12=12BC×EC+12EC×BD，
∴30=12×EC5+13，
∴CE=103．
22. （1） 16；110∘；70∘
【解析】如图 1 中，
∵ 四边形 ABCD 是平行四边形，
∴AD=BC=3，AB=CD=5，AD∥BC，
∴∠A=∠C=70∘，∠A+∠B=180∘，
∴∠B=110∘，
∴ 平行四边形 ABCD 的周长为 16．
（2） 如图 2 中，连接 AC 交 BD 于 O．
∵ 四边形 ABCD 是平行四边形，
∴CO=OA，
∵CF=FB，
∴OF∥AE，即 DF∥AE．
23. （1） 2400；2700
【解析】根据题意，
甲旅行社收费为 300×0.8×10=2400；
乙旅行社收费为 300×0.9×11−1=2700．
（2） 由题意可得，
甲旅行社的费用：y1=300×0.8x=240x，
乙旅行社的费用：y2=300×0.9×x−1=270x−270．
（3） 当 y19，
∴ 当公司外出人数大于 9 人时，选甲旅行社划算．
24. （1） 如图 ①，
∵ 四边形 ABCD 是正方形，
∴BC=CD，∠CBA=∠D=90∘，
∴∠D=∠CBF=∠BCD=90∘，
在 △CDE 和 △CBF 中，
∵CD=BC,∠D=∠CBF,DE=BF,
∴△CDE≌△CBFSAS，
∴CE=CF，∠DCE=∠BCF，
∴∠BCF+∠BCE=∠DCE+∠BCE=90∘，
∴△CEF 是等腰直角三角形．
（2） 如图 ②，过 M 作 MG⊥AF 于 G，
∵DE=BF=2，AB=6，
∴AE=4，AF=6+2=8，
∵∠FGM=∠FAE=90∘，∠FMG=∠FEA，
∴△FGM∽△FAE，
∴FGGM=FAAE=84=2，
∴FG=2GM，
设 GM=x，则 FG=2x，
∵ 四边形 ABCD 是正方形，
∴∠ABM=45∘，
∴△BGM 是等腰直角三角形，
∴BG=GM=x，
∴BG=BF=x=2，
∴GM=2，AG=6−2=4，
由勾股定理得：AM=22+42=25．
（3） 3
【解析】如图 ③，过 G 作 GP⊥CD 于 P，
由（1）知：∠CEF=45∘，
∵∠GNF=∠ENM=45∘，
∴∠EMN=90∘，
∴∠D=∠EMH=90∘，
∴∠GHC=∠DEC，
∴GP=BC=CD，∠D=∠GPH=90∘，
∴△GHP≌△CED，
∴CE=GH=35，
∵CD=6，
在 Rt△CED 中，由勾股定理得：DE=352−62=3．
25. （1） −6,0；0,3；6,0；y=−12x+3
【解析】对于 y=12x+3，由 x=0 得：y=3，
∴B0,3，
由 y=0 得：0=12x+3，解得 x=−6，
∴A−6,0，
∵ 点 C 与点 A 关于 y 轴对称，
∴C6,0，
设直线 BC 的函数解析式为 y=kx+b，
根据题意得：b=3,6k+b=0, 解得 k=−12,b=3,
∴ 直线 BC 的函数解析式为 y=−12x+3．
（2） ① 如图 1 所示：过点 B 作 BD⊥PQ，垂足为 D，
设 Mx,0，则 Px,12x+3，Qx,−12x+3，则 PQ=x，DB=x，
∵△PQB 的面积为 94，
∴12BD⋅QP12x⋅x=94，解得 x=322（负值舍去）．
∴M322,0．
② 如图 2 所示：当点 M 在 x 轴的正半轴上时，
∴OB∥QP，
∴∠BMP=∠OBM，
又 ∵∠BMP=∠BAC，
∴∠BAO=∠OBM，
∴OBOA=OMOB，即 36=OM3，解得 OM=32，
将 x=32 代入 y=12x+3 得：y=154，
∴P32,154．
如图 3 所示：当点 M 在 x 轴的负半轴上时，
∵OB∥OP，
∴∠BMP=∠OBM，
又 ∵∠BMP=∠BAC，
∴∠BAO=∠OBM，
∴OBOA=OMOB，即 36=OM3，解得 OM=32，
将 x=−32 代入 y=12x+3 得：y=94，
∴P−32,94，
∴ 点 P 的坐标为 −32,94 或 32,154．