

2019年浙教版数学九年级上学期期末专项复习卷(五)解直角三角形
展开一、选择题(共10小题;共50分)
1. 在 Rt△ABC 中,∠A=90∘,AB=3,BC=4,csB 等于
A. 34B. 74C. 35D. 45
2. 在 △ABC 中,∠C=90∘,若 csB=34,则 sinB 的值为
A. 35B. 45C. 74D. 73
3. 如图所示,小明为了测量其所在位置点 A 到河对岸点 B 之间的距离,沿着与 AB 垂直的方向走了 m m,到达点 C,测得 ∠ACB=α,那么 AB 等于
A. m⋅sinα mB. m⋅tanα mC. m⋅csα mD. mtanαm
4. 如图所示,在 Rt△ABC 中,CD 是斜边 AB 上的中线,已知 CD=2,AC=3,则 sinB 的值是
A. 23B. 32C. 34D. 43
5. 一把直尺与一把三角尺如图放置,若 sin∠1=22,则 ∠2 的度数为
A. 120∘B. 135∘C. 145∘D. 150∘
6. 如图所示,在 Rt△ABC 中,∠BAC=90∘,AD⊥BC 于点 D,若 BD=3,CD=2,则 tanB 等于
A. 32B. 23C. 62D. 63
7. 如图所示,每个小正方形大小相等.下列算式中,正确的是
A. sin∠1=55B. tan∠1=13C. cs∠1=1010D. tan∠1=12
8. 如图所示,小明同学用自制的直角三角形纸板 DEF 测量树的高度 AB,他调整自己的位置,设法使斜边 DF 保持水平,并且保持边 DE 与点 B 在同一直线上.已知纸板的两条直角边 DE=50 cm,EF=30 cm,测得边 DF 离地面的高度 AC=1.5 m,CD=20 m,则树高 AB 为
A. 12 mB. 13.5 mC. 15 mD. 16.5 m
9. 如图所示,在 ⊙O 上有定点 C 和动点 P,位于直径 AB 的异侧,过点 C 作 CP 的垂线,与 PB 的延长线交于点 Q.已知 ⊙O 的半径为 52,tan∠ABC=34,则 CQ 的最大值是
A. 5B. 154C. 253D. 203
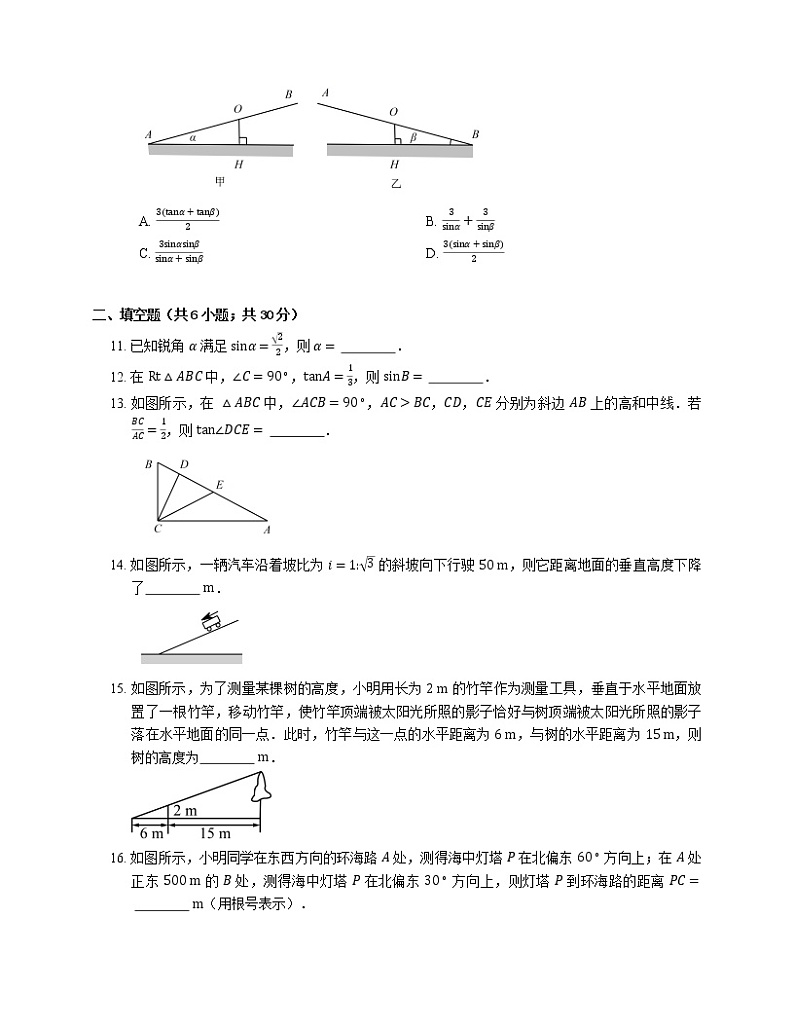
10. 已知跷跷板 AB 长 3 m,由于跷跷板的支撑点 O 偏离中点,所以当 A 端碰到地面时,AB 与地面的夹角为 α(如图甲所示),当 B 端碰到地面时,AB 与地面的夹角为 β(如图乙所示),则跷跷板 AB 的支撑点 O 到地面的高度 OH(用含 α,β 的式子表示)为
A. 3tanα+tanβ2B. 3sinα+3sinβ
C. 3sinαsinβsinα+sinβD. 3sinα+sinβ2
二、填空题(共6小题;共30分)
11. 已知锐角 α 满足 sinα=22,则 α= .
12. 在 Rt△ABC 中,∠C=90∘,tanA=13,则 sinB= .
13. 如图所示,在 △ABC 中,∠ACB=90∘,AC>BC,CD,CE 分别为斜边 AB 上的高和中线.若 BCAC=12,则 tan∠DCE= .
14. 如图所示,一辆汽车沿着坡比为 i=1:3 的斜坡向下行驶 50 m,则它距离地面的垂直高度下降了 m.
15. 如图所示,为了测量某棵树的高度,小明用长为 2 m 的竹竿作为测量工具,垂直于水平地面放置了一根竹竿,移动竹竿,使竹竿顶端被太阳光所照的影子恰好与树顶端被太阳光所照的影子落在水平地面的同一点.此时,竹竿与这一点的水平距离为 6 m,与树的水平距离为 15 m,则树的高度为 m.
16. 如图所示,小明同学在东西方向的环海路 A 处,测得海中灯塔 P 在北偏东 60∘ 方向上;在 A 处正东 500 m 的 B 处,测得海中灯塔 P 在北偏东 30∘ 方向上,则灯塔 P 到环海路的距离 PC= m(用根号表示).
三、解答题(共7小题;共91分)
17. 计算:
(1)3tan30∘−2cs45∘+sin260∘.
(2)sin30∘−12−2cs45∘+sin60∘⋅tan60∘.
(3)3tan30∘−2tan60∘cs60∘+4sin60∘.
(4)cs245∘+sin60∘⋅tan30∘−1−tan60∘2.
18. 如图所示,在 △ABC 中,∠C=90∘,sinA=45,AB=15,求 △ABC 的周长和 tanA 的值.
19. 某市在旧城改造中,计划在相距 6 km 的 A,B 两地间修一条东西方向的笔直的街道,但在 B 地北偏东 60∘ 方向的 C 处,有一个半径为 1.8 km 的文物保护单位(如图所示),又测得 A 地在 C 处的南偏东 52∘ 处.问这条笔直的街道是否会穿越这个文物保护单位?
(参考数据:sin52∘≈0.79,cs52∘≈0.62,tan52∘≈1.28,3≈1.73)
20. 如图所示,某小组发现 8 m 高的旗杆 DE 的影子 EF 落在了有一座圆弧形小桥的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高 1.6 m,测得其影长为 2.4 m,同时测得 EG 的长为 3 m,HF 的长为 1 m,测得拱高(GH 的中点到弦 GH 的距离,即 MN 的长)为 2 m,求小桥所在圆的半径.
21. 在一个风和日丽的周末,小东和小芸一起到郊外放风筝.他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的 C 处(如图所示).现已知风筝 A 的引线(线段 AC)长 20 m,风筝 B 的引线(线段 BC)长 24 m,在 C 处测得风筝 A 的仰角为 60∘,风筝 B 的仰角为 45∘.
(参考数据:sin45∘≈0.707,cs45∘≈0.707,tan45∘=1,sin60∘≈0.866,cs60∘=0.5,tan60∘≈1.732)
(1)通过计算,比较风筝 A 与风筝 B 哪个离地面更高.
(2)求风筝 A 与风筝 B 的水平距离.(精确到 0.01 m)
22. 如图所示,小明在距地面 45 m 高(即 PH=45 m)的窗口 P 处进行观测,测得山坡上 A 处的俯角为 15∘,山脚 B 处的俯角为 60∘,已知该山坡的坡度 i(即 tan∠ABC)为 1:3,点 P,H,B,C,A 在同一个平面上,点 H,B,C 在同一条直线上,且 PH⊥HC.
(1)山坡坡角(即 ∠ABC)的度数等于 度.
(2)求 A,B 两点间的距离.(结果精确到 1 m,参考数据:3≈1.732)
23. 给出图形新定义:如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“特别三角形”.
(1)请用直尺和圆规画一个“特别三角形”(选用适当边长;不写画法,保留作图痕迹).
(2)如图甲所示,在 Rt△ABC 中,已知 ∠C=90∘,tanA=32,判断 △ABC 是否为“特别三角形”,若是,请给出证明;若不是,请说明理由.
(3)如图乙所示,已知菱形 ABCD 的边长为 a,∠ABC=60∘,点 P,Q 从点 A 同时出发,以相同的速度分别沿折线 A→B→C 和 A→D→C 向终点 C 运动.记点 P 经过的路程为 s,当 △APQ 是“特别三角形”时,试求 as 的值.
答案
第一部分
1. A
2. C
3. B【解析】tanα=ABm,AB=m⋅tanα.
4. C【解析】sinB=ACAB=AC2CD=34.
5. B
【解析】由 sin∠1=22,可知 ∠1=45∘,
∴∠2=135∘.
6. D【解析】如图所示,令 AC=x,AB=y.
在 △ABC 中,S△ABC=12xy=12BC⋅AD,
即 AD=xy5,
则 tanB=xy=xy53,
解得 y2=15,
则 y=15y>0,
又 ∵∠B=∠DAC,
则 tan∠DAC=2xy5=10xy=xy,
解得 x2=10,
则 x=10x>0,
∴tanB=xy=1015=63.
7. B
8. B【解析】易证 △DEF∽△DCB,
∴ BCEF=DCDE.
∵ DE=50 cm=0.5 m,EF=30 cm=0.3 m,AC=1.5 m,CD=20 m,
∴ BC0.3=200.5,
解得 BC=12m.
∴ AB=AC+BC=1.5+12=13.5m.
9. D【解析】∵ AB 为 ⊙O 的直径,
∴ AB=5,∠ACB=90∘.
∵ tan∠ABC=ACBC,
∴ ACBC=34,
∵ CP⊥CQ,
∴ ∠PCQ=90∘,而 ∠A=∠P,
∴ △ACB∽△PCQ,
∴ ACPC=BCCQ,
∴ CQ=BCAC⋅PC=43PC,当 PC 最大时,CQ 最大,即 PC 为 ⊙O 的直径时,CQ 最大,此时 CQ=43×5=203.
10. C
【解析】AO=OHsinα,BO=OHsinβ,
∴ AO+BO=OHsinα+OHsinβ=3.则 OH=3sinαsinβsinα+sinβ.
第二部分
11. 45∘
12. 31010
【解析】令 BC=1,AC=3.
则在 Rt△ABC 中,AB=10,sinB=ACAB=310=31010.
13. 34
【解析】由 BCAC=12,可设 BC=x,则 AC=2x,
∵ 在 Rt△ABC 中,∠ACB=90∘,CD,CE 分别为斜边 AB 上的高和中线,
可分别求得 AB=AC2+BC2=5x,CD=AC×BCAB=255x,BD=BC2−CD2=55x,BE=AB2=52x,DE=BE−BD=3510x,
∴tan∠DCE=DECD=34.
14. 25
【解析】设垂直高度下降了 xm,则水平前进了 3xm.
根据勾股定理得 x2+3x2=502,
解得 x=25.
15. 7
【解析】如图所示,
AD=6 m,AB=21 m,DE=2 m,
∵ DE∥BC,
∴ △ADE∽△ABC.
∴ DEBC=ADAB,即 2BC=621,解得 BC=7 m.
16. 2503
【解析】由已知得,在 Rt△PBC 中,∠PBC=60∘,PC=BCtan60∘=3BC.
在 Rt△APC 中,∠PAC=30∘,AC=3PC=3×3BC=3BC=500+BC,
解得 BC=250.
∴ PC=2503m.
第三部分
17. (1) 34.
(2) 34.
(3) 0.
(4) 2−3.
18. 在 Rt△ABC 中,
∵sinA=BCAB=BC15=45,
∴BC=12,AC=AB2−BC2=152−122=9,
则周长
C△ABC=AB+BC+AC=15+12+9=36,
tanA=BCAC=129=43.
19. 过点 C 作 CD⊥AB 于点 D,
设 CD=xm,
在 Rt△ADC 中,tan∠ACD=ADCD,AD=xtan52∘,
在 Rt△BDC 中,tan∠BCD=BCCD,BD=xtan60∘=3x,
∴ 3x+xtan52∘=6,
∴ 1.73x−1.28x=6,
∴ x≈2.
∵ 2 km>1.8 km,
∴ 不会穿越这个文物保护单位.
20. 由相似得 DEEF=1.62.4,解得 EF=12.
∵ EG=3,HF=1,
∴ GH=EF−EG−HF=8.
由垂径定理得:GM=12GH=4.
又 MN=2,
设半径 OG=R,则 OM=R−2.
在 Rt△OMG 中,由勾股定理得:OM2+MG2=OG2,
因此 R−22+42=R2,解得 R=5.
因此小桥所在圆的半径为 5 m.
21. (1) 在 Rt△ACD 中,sin60∘=ADAC=AD20≈0.866,
解得 AD≈17.32m.
在 Rt△BCE 中,sin45∘=BEBC=BE24≈0.707,
解得 BE≈16.97m,
则 AD>BE,A 的风筝离地面更高.
(2) 风筝 A 与风筝 B 的水平距离即为 ED 的长,ED=24⋅cs45∘−20⋅cs60∘≈6.97m.
22. (1) 30
(2) 由题意知:∠PBH=60∘,∠APB=45∘,
∵∠ABC=30∘,
∴∠ABP=90∘.
在 Rt△PHB 中,PB=PHsin∠PBH=4532=303.
在 Rt△PBA 中,AB=PB=303≈52m.
答:A,B 两地间的距离为 52 m.
23. (1) 如图所示.
(2) 是特别三角形.证明如下:
∵ tanA=32,∠C=90∘,
∴ BC:AC=3:2,设 BC=3k,AC=2k,取 AC 的中点 D,连接 BD,
∴ BD=k2+3k2=2k.
∴ BD=AC.
∴ △ABC 是特别三角形.
(3) ①若 P 在 AB 上,
∵ ∠ABD=30∘,∠BAD=120∘,△APQ 是等腰三角形,无论底边上的中线,还是腰上的中线都不符合要求,不存在特别三角形.
②若 P 在 BC 上,分两种情况:
(ⅰ)一种情况是 PQ 为底边,如图甲所示,
AH=PQ.
∴ △APQ 是等腰三角形,
∴ AH=2PH,设 AH=x,则 CH=a−x,PC=2a−x,PH=3a−x=12x,
解得 x=23a1+23,而 s=a+a−PC=2x,
∴ as=a2x,将 x=23a1+23 代入解得 as=1+2343(以上是用解直角三角形方法).
(ⅱ)另一种情况是 AP 为底边,如图2所示,QM=AP=AQ,作 NQ⊥AP 于点 N,
∵ △AMQ 是等腰三角形,AN=14AP=14AQ,
∴ NQ=AQ2−AN2=15AN,
∴ tan∠NPQ=NQPN=15AN3AN=153,
又 ∵ tan∠NPQ=AHPH=12AK32PC=12s322a−s=153,
解得 as=51+52=1+525.
【解析】(ⅰ)解法二:用相似三角形性质:延长 AB 交 QP 延长线于点 K,则 △AKH∽△CPH.
∴ CPAK=CHAH=CH2PH=CH2×3CH=123,
解得 CPAK=2a−ss,
∴ 2a−ss=123,
解得 as=1+2343.
2019年浙教版数学九年级上学期期末专项复习卷(一)二次函数: 这是一份2019年浙教版数学九年级上学期期末专项复习卷(一)二次函数,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2019年浙教版数学九年级上学期期末专项复习卷(四)相似三角形: 这是一份2019年浙教版数学九年级上学期期末专项复习卷(四)相似三角形,共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2019年浙教版数学九年级上学期期末专项复习卷(三)圆的基本性质: 这是一份2019年浙教版数学九年级上学期期末专项复习卷(三)圆的基本性质,共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












