

九年级数学上册试题 期中复习卷3-北师大版(含答案)
展开
这是一份九年级数学上册试题 期中复习卷3-北师大版(含答案),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(本大题共14个小题,每题2分,共28分)
1.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )
A.B.C.D.
2.下面性质中菱形有而矩形没有的是( )
A.邻角互补B.内角和为360°
C.对角线相等D.对角线互相垂直
3.一元二次方程已知方程配方可变形为 ( )
A.B.C.D.
4.关于的一元二次方程根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
5.下列能够判定一个四边形是正方形的条件是( )
①一组邻边相等且对角线相等并互相平分;
②对角线互相垂直平分;
③四条边相等且四个内角也相等;
④对角线相等的菱形.
A.①②④B.①③④C.③④D.①②③④
6.从1到9这9个自然数中任取一个,既是2的倍数,又是3的倍数的概率是( )
A.B.C.D.
7.如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是
A.矩形B.菱形C.正方形D.等腰梯形
8.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2,∠DAO=30°,则FC的长度为( )
A.1B.2
C.D.
9.从箱子中摸出红球的概率为,已知口袋中红球有个,则袋中共有球( )个
A.B.C.D.
10.若关于的一元二次方程有一根为0,则m的值等于( )
A.1B.0C.1或2D.2
11.一个盒子里装有若干个红球和白球,每个球除颜色以外都相同.5位同学进行摸球游戏,每位同学摸10次(摸出1球后放回,摇匀后再继续摸),其中摸到红球数依次为8,5,9,7,6,则估计盒中红球和白球的个数是( )
A.红球比白球多B.白球比红球多C.红球,白球一样多D.无法估计
12.定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )
A.方有两个相等的实数根B.方程有一根等于0
C.方程两根之和等于0D.方程两根之积等于0
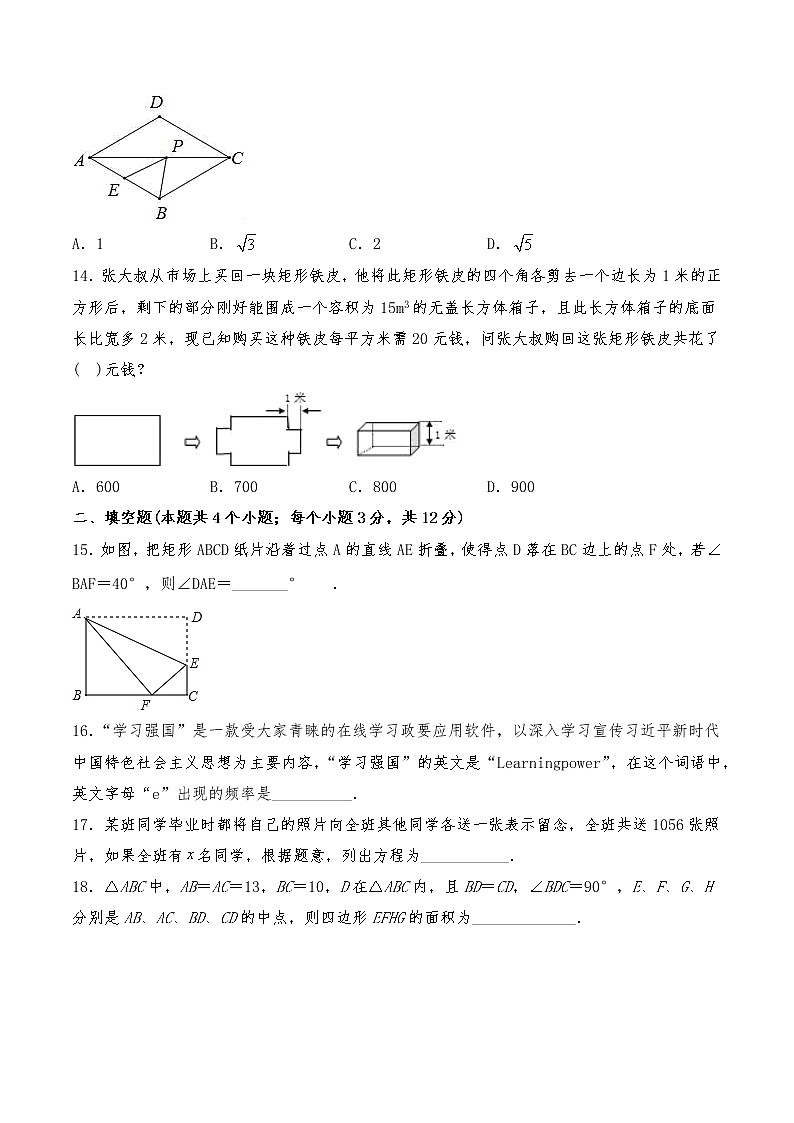
13.如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )
A.1B.C.2D.
14.张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了( )元钱?
A.600B.700C.800D.900
二、填空题(本题共4个小题;每个小题3分,共12分)
15.如图,把矩形ABCD纸片沿着过点A的直线AE折叠,使得点D落在BC边上的点F处,若∠BAF=40°,则∠DAE=_______°.
16.“学习强国”是一款受大家青睐的在线学习政要应用软件,以深入学习宣传习近平新时代中国特色社会主义思想为主要内容,“学习强国”的英文是“Learningpwer”,在这个词语中,英文字母“e”出现的频率是__________.
17.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有名同学,根据题意,列出方程为___________.
18.△ABC中,AB=AC=13,BC=10,D在△ABC内,且BD=CD,∠BDC=90°,E、F、G、H分别是AB、AC、BD、CD的中点,则四边形EFHG的面积为_____________.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.选用适当的方法解下列方程
(1)2x2﹣5x﹣8=0 (2)(x﹣2)(2x﹣3)=2(x﹣2)
20.如图,矩形中,,将矩形绕点顺时针旋转得到矩形.设旋转角为,此时点恰好落在边上,连接.
(1)当恰好是中点时,此时________;
(2)若,求旋转角及的长.
21.不透明的袋子中装有大小、质地完全相同的2个白球和2个黑球.
(1) 先从袋中投出1个球后放回,混合均匀后再摸出1个球,则第一次摸到白球,第二次摸到黑球的概率为P1为__________;
(2) 若第一次从袋子中摸出1个球后不放回,第二次再摸出1个球,则两次摸到的球中有1个白球和1个黑球的概率P2是多少?(请用画树形图或列表法求出结果)
22.如图,在中,,点为斜边边上的中点,,.
(1)求证:四边形ADCE是菱形
(2)连接DE,若,.求证:是等边三角形.
23.某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间正好可以住满.每个房间每天的定价每增加10元,就会有一个房间空闲.已知有游客入住的房间,宾馆每天需对每个房间支出50元的各种费用.
(1)若某天宾馆的入住量为58个房间,则该天宾馆的利润为________元;
(2)求宾馆每天房间入住量达到多少个时,每天的利润为11000元.
24.阅读下面的解答过程,求的最小值.
解:
∵即的最小值为0
∴的最小值为4.
仿照上面的解答过程,
(1)求的最小值
(2)求的最大值
25.2020年6月14日是第17个世界献血者日,今年的活动主题是“安全血液拯救生命”,使用的活动口号为“献血,让世界更健康”,意在关注个人献血为改善社区其他人的健康所做的贡献.为此,成都市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”,“B型”,“AB型”,“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
(1)这次随机抽收的献血者人数为 人,m= ;
(2)求x,y的值;
(3)请你根据抽样结果回答:从献血者人群中任抽取一人.其血型是O型的概率是多少?若这次活动中有8000人义务献血,大约有多少人是O型血?
26.如图,正方形ABCD中,E是CD边的中点,F是BC边上一点,∠FAE=∠DAE.
(1)求证:AF=AD+CF;
(2)已知正方形ABCD的边长为4.
①求AF之长;
②若P是AE上一点,且△DEP是等腰三角形,则线段EP的长为________.
答案
一、选择题
1.A.2.D.3.D.4.A.5.B.6.A.7.B.8.A.9.B.
10.B.11.A.12.C.13.B.14.B.
二、填空题
15.25
16.
17.x(x-1)=1056
18..
三、解答题
19.解:(1)在此方程中,a=2,b=﹣5,c=﹣8,
所以,
∴,
∴x1=,x2=;
(2)移项,得(x﹣2)(2x﹣3)-2(x﹣2)=0,
原方程可变形为:,
即,
∴x-2=0或2x-5=0,
解得:x1=2,x2=.
20.解:(1)∵四边形是矩形,
∴,,当恰好是中点时,,
∴,
∴,
∴,即当恰好是中点时,此时.
故答案为:60°.
(2)∵四边形是矩形,
∴,
∴.由旋转的性质得,
∴,
∴,即旋转角为30°.
作于点.
则.
21.解:(1)画树状图得:
∵共有16种等可能的结果,第一次摸到白球,第二次摸到黑球的有4种情况,
∴第一次摸到白球,第二次摸到黑球的概率P1=;
(2)画树状图得:
∵共有12种等可能的结果,一次摸到白球,二次摸到黑球的有8种情况,
∴两次摸到的球中有1个白球和1个黑球的概率是:.
22.
(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
又∵∠ACB=90°,D是AB的中点,
∴CD=AB=BD=AD,
∴平行四边形ADCE是菱形;
(2)解:∵在Rt△ABC中,∠ACB=90°,AC=,BC=1,
∴AB==2
∴∠CAB=30°,
∵四边形ADCE是菱形,
∴∠EAD=2∠CAB=60°,AE=AD,
∴△ADE是等边三角形.
23.解:(1)[200+10×(60﹣58)﹣50]×58=9860(元).
故答案为:9860.
(2)设每个房间每天的定价增加了x元,则每天可入住(60﹣)个房间,
依题意,得:(60﹣)(200+x﹣50)=11000,
化简得:x2﹣450x+20000=0,
解得:x1=50,x2=400,
∴60﹣=55或20.
答:每天房间入住量达到55个或20个时,利润为11000元.
24.解:(1)
∵
∴
∴的最小值是3.
(2)
∵
∴
∴的最大值为5
25.解:(1)∵10÷10%=100,
20÷100=20%,
答:这次随机抽收的献血者人数为100人,m=20;
故答案为:100,20;
(2)x=100×25%=25,
y=100﹣25﹣20﹣10=45;
(3)血型是O型的概率是:
=,
所以8000×=3600(人).
答:从献血者人群中任抽取一人.其血型是O型的概率是,若这次活动中有8000人义务献血,大约有3600人是O型血.
26.(1)证明:如图1,过E点作EG⊥AF,垂足为G,连接EF,
(也可延长AE、BC交于P,用全等和等腰三角形知识解决),
∵EG⊥AF,
∴∠EGF=∠AGE=90°,
∵四边形ABCD是正方形,
∴∠C=∠D=90°,
在△AGE和△ADE中,
∴△AGE≌△ADE(AAS),
∴AD=AG,GE=DE,
∵E是CD边的中点,
∴CE=DE,
∴GE=CE,
在Rt△EGF和Rt△ECF中,
∴Rt△EGF≌Rt△ECF(HL),
∴GF=CF,
∵AF=AG+GF,
∴AF=AD+CF;
(2)解:①设CF=x,则BF=4-x,AF=4+x,
在Rt△ABF中,AB2+BF2=AF2,
∴42+(4-x)2=(4+x)2,
解得:x=1,
∴AF=4+x=4+1=5;
②分三种情况:
i)如图2,PD=DE,过D作DG⊥AE于G,
∴EP=2EG,
Rt△ADE中,AD=4,DE=2,
∴,
∴,
即,
∴,
由勾股定理得:,
∴EP=2EG=;
ii)如图3,EP=DE=2;
iii)如图4,PD=PE,过P作PM⊥DE于M,则DM=EM,
∵AD⊥CD,PM⊥DE,
∴AD∥PM,
∴AP=PE,
∵AE=,
∴EP=,
综上,EP的长是2或或.
相关试卷
这是一份七年级数学下册试题 期末复习卷3-北师大版(含答案),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份九年级数学上册试题 期中复习卷2-北师大版(含答案),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份九年级数学上册试题 期中复习卷1-北师大版(含答案),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








