高中数学2.1 等式与不等式的性质课文配套课件ppt

这是一份高中数学2.1 等式与不等式的性质课文配套课件ppt，共21页。PPT课件主要包含了等式的性质，等式有什么性质，★对称性，★传递性，★加减性，★同乘性，★同除性，恒等式，十字相乘法，方程的解集等内容，欢迎下载使用。

有只狡猾的狐狸平时总喜欢戏弄其他动物,有一天它遇见老虎,狐狸说:“我发现了2和5可以相等.我这里有一个方程5x-2=2x-2.等式两边同时加上2,得5x-2+2=2x-2+2,即5x=2x,①等式两边同时除以x,得5=2②”.老虎瞪大了眼睛,一脸的疑惑.你认为狐狸的说法正确吗?
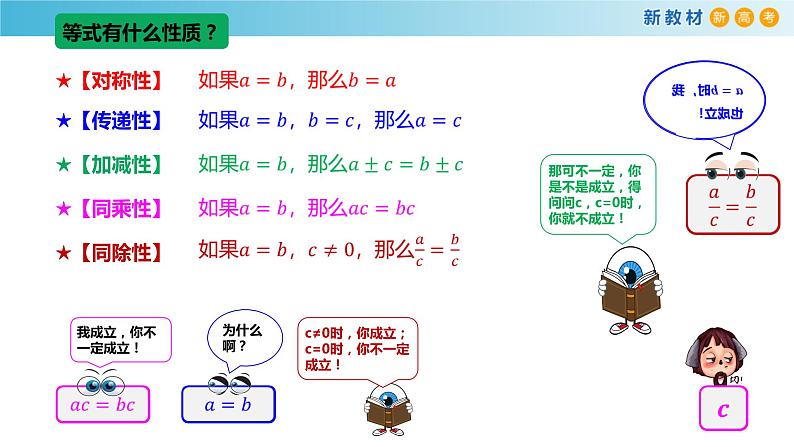
（1）等式的两边同时加上同一个数或代数式，等式仍成立；（2）等式的两边同时乘以同一个不为零的数或代数式，等式仍成立.
我成立，你不一定成立！
c≠0时，你成立；c=0时，你不一定成立！
那可不一定，你是不是成立，得问问c，c=0时，你就不成立！
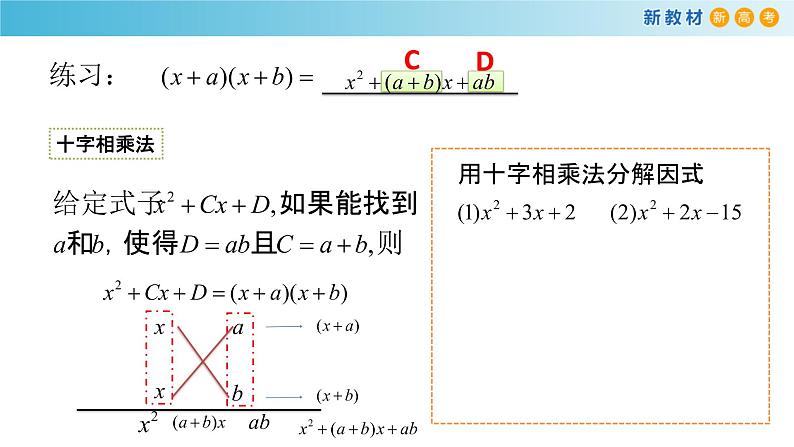
分解因式:(1)x2-25; (2)a2-6a+9; (3)4m(x-y)-8n(y-x); (4)(a2+4)2-16a2.分析:掌握提取公因式法和公式法是解题的关键.解:(1)x2-25=(x+5)(x-5); (2)a2-6a+9=(a-3)2;(3)4m(x-y)-8n(y-x)=4(x-y)(m+2n);(4)(a2+4)2-16a2=(a2+4+4a)(a2+4-4a)=(a+2)2(a-2)2.反思感悟 分解因式的常用方法(1)平方差公式法; (2)完全平方公式法; (3)提取公因式法; （4）十字相乘法
反思感悟十字相乘法分解因式易误点用十字相乘法分解因式,还要注意避免以下两种错误:一是没有验证交叉相乘的两个积的和是否等于一次项系数;二是由十字相乘写出的因式漏写字母.
变式训练(1)x2+10x+16分解因式为(　　)A.(x+2)(x+8)B.(x-2)(x+8)C.(x+2)(x-8)D.(x-2)(x-8)(2)x2-13xy-30y2分解因式为(　　)A.(x-3y)(x-10y) B.(x+15y)(x-2y)C.(x+10y)(x+3y)D.(x-15y)(x+2y)(3)6x2-29x+35分解因式为(　　)A.(2x-7)(3x-5)B.(3x-7)(2x-5)C.(3x-7)(2x+5)D.(2x-7)(3x+5)
解析:(1)x2+10x+16=(x+2)(x+8).
(2)x2-13xy-30y2=(x-15y)(x+2y).
(3)6x2-29x+35=(3x-7)(2x-5).
答案:(1)A　(2)D　(3)B
1.思考(1)一元一次方程kx+b=0(k≠0)的根是什么?(2)一元二次方程ax2+bx+c=0(a≠0)的求根公式是什么?2.填空(1)方程的解(或根)是指 .(2)一般地,把一个方程所有解组成的集合称为这个方程的解 .3.做一做 求方程x2+3x+2=0的解集. 解:∵x2+3x+2=0,∴(x+1)(x+2)=0, ∴x=-1或x=-2,∴方程的解集为{-1,-2}.
能使方程左右两边相等的未知数的值
例4：求方程x(x-2)+x-2=0的解集.分析将方程左边整理化成两个一次因式乘积的形式,进而求解.解:把方程左边因式分解,得(x-2)(x+1)=0,从而,得x-2=0或x+1=0,所以x1=2,x2=-1.所以方程的解集为{-1,2}.反思感悟因式分解法解一元二次方程用因式分解法解一元二次方程的一般步骤是:①将方程右边的各项移到方程左边,使方程右边为0;②将方程左边分解为两个一次因式的乘积的形式;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就是原方程的解.
延伸探究请用求根公式求解本例方程的解集.
解:原方程可化为x2-x-2=0,
∴x1=2,x2=-1,∴方程的解集为{-1,2}.
数形结合思想的应用典例 二次函数y=-x2+(m-1)x+m的图像与y轴交于点(0,3).(1)求出m的值并画出此二次函数的图像.(2)求此二次函数的图像与x轴的交点及函数图像顶点的坐标.(3)x取什么值时,函数图像在x轴上方.
解:(1)由二次函数y=-x2+(m-1)x+m的图像与y轴交于点(0,3),得m=3.∴二次函数为y=-x2+2x+3.图像如图所示.
(2)由-x2+2x+3=0,得x1=-1,x2=3.∴二次函数图像与x轴的交点为(-1,0),(3,0).∵y=-x2+2x+3=-(x-1)2+4.∴函数图像的顶点坐标为(1,4).(3)由图像可知:当-1方法点睛本题是二次函数图像和性质的简单应用,要注意把握二次函数图像的特征,尤其是顶点、对称轴和开口方向.
1.下列由等式的性质进行的变形,错误的是(　　)
B.如果a=3,那么a2=9C.如果a=3,那么a2=3aD.如果a2=3a,那么a=3
解析:如果a=3,那么 ,正确,故选项A不符合题意;如果a=3,那么a2=9,正确,故选项B不符合题意;如果a=3,那么a2=3a,正确,故选项C不符合题意;如果a=0时,两边都除以a,无意义,故选项D符合题意.答案:D
2.下列分解因式正确的是(　　)A.x2+y2=(x+y)(x-y)B.m2-2m+1=(m+1)2C.a2-16=(a+4)(a-4)D.x3-x=x(x2-1)解析:A.原式不能分解,错误;B.原式=(m-1)2,错误;C.原式=(a+4)(a-4),正确;D.原式=x(x2-1)=x(x+1)(x-1),错误.答案:C3.若x=3是方程3x-a=0的解,则a的值是　　　　. 解析:把x=3代入方程3x-a=0得9-a=0,解得a=9.答案:9