

鲁教版八年级上册数学 期末达标检测卷
展开期末达标检测卷
一、选择题(本大题共12道小题,每小题3分,满分36分)
1.2020年太原正式步入“地铁时代”,太原轨道交通近期建设的1、2、3号线在全国是第338条线路.下面是中国四个城市的地铁图标,其中是中心对称图形的是( )
2.若a+b=3,则a2+6b-b2的值为( )
A.3 B.6 C.9 D.12
3.把多项式3(x-y)2+2(y-x)3分解因式,结果正确的是( )
A.(x-y)2(3-2x-2y) B.(x-y)2(3-2x+2y)
C.(x-y)2(3+2x-2y) D.(y-x)2(3+2x+2y)
4.若分式的值为0,则x的值为( )
A.±2 B.2 C.-2 D.-1
5.一个多边形的内角和与外角和相加之后的结果是2 520°,则这个多边形的边数为( )
A.12 B.13 C.14 D.15
6.方程=的解为( )
A.x=-2 B.x=4
C.x=0 D.x=6
7.某班50人一周内在线学习数学的时间如图所示,则以下叙述正确的是( )
A.全班同学在线学习数学的平均时间为2.5 h
B.全班同学在线学习数学时间的中位数为2 h
C.全班同学在线学习数学时间的众数为20 h
D.全班超过半数同学每周在线学习数学的时
间超过3 h
8.若分式方程-=6有增根,则它的增根是( )
A.0 B.1 C.-1 D.1或-1
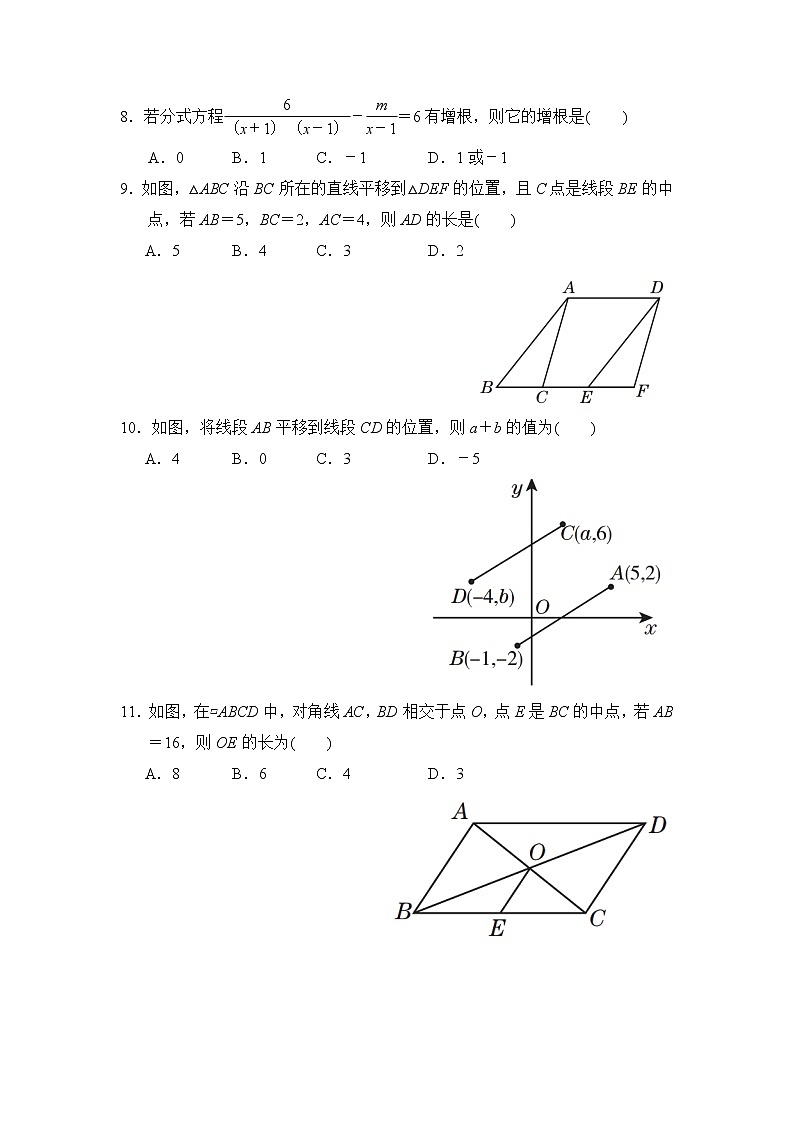
9.如图,△ABC沿BC所在的直线平移到△DEF的位置,且C点是线段BE的中点,若AB=5,BC=2,AC=4,则AD的长是( )
A.5 B.4 C.3 D.2
10.如图,将线段AB平移到线段CD的位置,则a+b的值为( )
A.4 B.0 C.3 D.-5
11.如图,在▱ABCD中,对角线AC,BD相交于点O,点E是BC的中点,若AB=16,则OE的长为( )
A.8 B.6 C.4 D.3
12.如图,E,F分别是平行四边形ABCD的边AD,BC上的点,且BE∥DF,AC分别交BE,DF于点G,H.下列结论:①四边形BFDE是平行四边形;②△AGE≌△CHF;③BG=DH;④S△AGE︰S△CDH=GE︰DH.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6道小题,每小题3分,满分18分)
13.如果a2-2a=0,则2a2 020-4a2 019+2 020的值为________.
14.使代数式÷有意义的x的取值范围是________.
15.一组数据3,2,x,2,6,3的唯一众数是2,则这组数据的方差为________.
16.如图,在▱ABCD中,对角线AC与BD相交于点O,且AB⊥AC,∠DAC=45°,如果AC=2,那么BD的长是________.
17.如图,在平面直角坐标系中,点A(3,0),点B(0,2),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,则线段OC的长度为________.
18.如图,在▱ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边CD的中点,DG⊥AE,垂足为G,若DG=,则AE的长为________.
三、解答题(本大题共7道小题,满分66分)
19.(9分)分解因式:
(1)x3-x; (2)2a2-4a+2; (3)m4-2m2+1.
20.(7分)先化简,再求值:÷+,其中x的值为方程2x=5x-1的解.
21.(8分)某校八年级开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
(1)根据统计图直接写出上表中a,b,c的值;
(2)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定.
22.(10分)如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E,F在CB上,且∠1=∠2,∠3=∠4.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC是否随之变化?若变化,找出规律或求出其变化范围;若不变,求出这个比.
23.(10分)2020年初,市场上防护口罩出现热销.某药店用3 000元购进甲、乙两种不同型号的口罩共1 100只进行销售,已知购进甲种口罩与乙种口罩的费用相同,购进甲种口罩单价是乙种口罩单价的1.2倍.
(1)求购进的甲,乙两种口罩的单价各是多少;
(2)若甲、乙两种口罩的进价不变,该药店计划用不超过7 000元的资金再次购进甲、乙两种口罩共2 600只,求甲种口罩最多能购进多少只.
24.(10分)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F,AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF.
25.(12分)已知在△ABC中,AB=AC,点D在BC上,以AD,AE为腰作等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA的延长线于M,连接BM.
(1)求证:△BAD≌△CAE;
(2)若∠ABC=30°,求∠MEC的度数;
(3)求证:四边形MBDE是平行四边形.
答案
一、1.C 2.C 3.B 4.C 5.C 6.B
7.B
8.B 【点拨】分式方程的最简公分母为(x+1)(x-1),去分母得6-m(x+1)=6(x+1)(x-1).由分式方程有增根,得到(x+1)(x-1)=0,即x=1或x=-1,把x=-1代入整式方程得6=0,无解,则它的增根是1.故选B.
9.B 【点拨】由平移的性质可知,AD=BE,∵BC=CE,BC=2,∴BE=4,∴AD=4.故选B.
10.A 【点拨】由题意知,线段AB向左平移3个单位长度,再向上平移4个单位长度得到线段CD,∴a=5-3=2,b=-2+4=2,∴a+b=4.故选A.
11.A 【点拨】∵在▱ABCD中,对角线AC,BD相交于点O,∴点O是AC的中点.又∵点E是BC的中点,∴EO是△ABC的中位线,∴EO=AB=8.故选A.
12.D 【点拨】∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,AD=BC,
∵BE∥DF,∴四边形BFDE是平行四边形,故①正确;
∵四边形BFDE是平行四边形,
∴BF=DE,DF=BE,∴AE=FC,
∵AD∥BC,BE∥DF,∴∠DAC=∠ACB,∠ADF=∠DFC,∠AEB=∠ADF,
∴∠AEB=∠DFC,
∴△AGE≌△CHF(ASA),
故②正确;∵△AGE≌△CHF,∴GE=FH,
∵BE=DF,∴BG=DH,故③正确;
∵△AGE≌△CHF,∴S△AGE=S△CHF,
∵S△CHF︰S△CDH=FH︰DH,
∴S△AGE︰S△CDH=GE︰DH,故④正确.故选D.
二、13.2 020
14.x≠±3且x≠-4
15.2 【点拨】∵数据3,2,x,2,6,3的唯一众数是2,∴x=2.∴3,2,2,2,6,3的平均数为×(3+2+2+2+6+3)=3,则这组数据的方差为×[(2-3)2×3+(3-3)2×2+(6-3)2]=2.
16.2 【点拨】∵四边形ABCD是平行四边形,∴AD∥BC,OB=OD,OA=AC=1,∴∠ACB=45°.∵AB⊥AC,∴△ABC是等腰直角三角形,∴AB=AC=2.在Rt△AOB中,根据勾股定理,得OB=,∴BD=2BO=2.
17. 【点拨】如图,作CH⊥x轴于H.
∵A(3,0),B(0,2),∴OA=3,OB=2,∵∠AOB=∠BAC=∠AHC=90°,∴∠BAO+∠HAC=90°,∠HAC+∠ACH=90°,∴∠BAO=∠ACH.∵AB=AC,∴△ABO≌△CAH(AAS),∴AH=OB=2,CH=OA=3,∴OH=OA+AH=3+2=5,∴OC===.
18.8 【点拨】∵AE为∠DAB的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD为平行四边形,
∴AD∥BC,DC∥AB,DC=AB.
∵DC∥AB,
∴∠BAE=∠DFA,∴∠DAE=∠DFA,
∴AD=FD.
又∵DG⊥AE,
∴AG=FG,即AF=2AG.
∵F为DC的中点,∴DF=CF,
∴AD=DF=DC=AB=3.
在Rt△ADG中,根据勾股定理得AG=2,则AF=2AG=4.
∵AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF.
在△ADF和△ECF中,
∴△ADF≌△ECF(AAS),
∴AF=EF,则AE=2AF=8.
三、19.解:(1)x3-x=x(x2-1)=x(x+1)(x-1);
(2)2a2-4a+2=2(a2-2a+1)=2(a-1)2;
(3)m4-2m2+1=(m2-1)2=(m+1)2(m-1)2.
20.解:÷+
=÷+
=·+
=+
=.
解方程2x=5x-1,得x=.
当x=时,原式=-.
21.解:(1)a=85;b=80;c=85.
(2)求知班成绩的方差为×[(70-85)2+(75-85)2+(80-85)2+2×(100-85)2]=160.
∵70<160,∴爱国班的成绩比较稳定.
22.解:(1)∵CB∥OA,
∴∠C+∠COA=180°.
∵∠C=120°,
∴∠COA=180°-∠C=180°-120°=60°.
∵∠1=∠2,∠3=∠4,
∴∠COA=2∠1+2∠4=2(∠1+∠4)=2∠EOB.
∴∠EOB=∠COA=×60°=30°.
(2)不变化.
∵CB∥OA,
∴∠OBC=∠2,∠OFC=∠FOA.
又∵∠1=∠2,∴∠OBC=∠1,
∴∠OFC=2∠1,
∴∠OBC∠OFC=∠12∠1=12.
23.解:(1)3 000÷2=1 500(元).
设乙种口罩的单价为x元,则甲种口罩的单价为1.2x元,由题意,得
+=1 100,
解得x=2.5,
经检验,x=2.5是原方程的解,且符合题意,
∴1.2x=3.
∴甲种口罩的单价为3元,乙种口罩的单价为2.5元.
(2)设该药店购进甲种口罩a只,则购进乙种口罩(2 600-a)只,
由题意,得3a+2.5(2 600-a)≤7 000,
解得a≤1 000.
∴甲种口罩最多能购进1 000只.
24.(1)解:∵AE⊥BD,∴∠AEO=90°.
∵∠AOE=50°,∴∠EAO=40°.
∵AC平分∠DAE,
∴∠DAC=∠EAO=40°.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ACB=∠DAC=40°.
(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC.
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°.
∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS),
∴AE=CF.
25.(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∴∠BAC=180°-2∠ABC.
∵以AD,AE为腰作等腰三角形ADE,
∴AD=AE,∴∠ADE=∠AED,
∴∠DAE=180°-2∠ADE.
∵∠ADE=∠ABC,∴∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△BAD≌△CAE(SAS).
(2)解:∵AB=AC,
∴∠ACB=∠ABC=30°.
∵△BAD≌△CAE,
∴∠ABD=∠ACE=30°,
∴∠ECB=∠ACB+∠ACE=60°.
∵EM∥BC,∴∠MEC+∠ECD=180°,
∴∠MEC=180°-60°=120°.
(3)证明:∵△BAD≌△CAE,
∴DB=CE,∠ABD=∠ACE.
∵AB=AC,
∴∠ABD=∠ACB,
∴∠ACB=∠ACE.
∵EM∥BC,
∴∠EMC=∠ACB,
∴∠ACE=∠EMC,
∴ME=EC,
∴DB=ME.
又∵EM∥BD,
∴四边形MBDE是平行四边形.
沪科版数学八年级上册期末达标检测卷: 这是一份沪科版数学八年级上册期末达标检测卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北师大版数学八年级上册期末达标检测卷: 这是一份北师大版数学八年级上册期末达标检测卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
苏科版八年级上册数学 期末达标检测卷: 这是一份苏科版八年级上册本册综合同步训练题,共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













