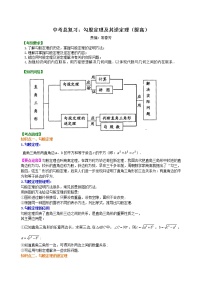
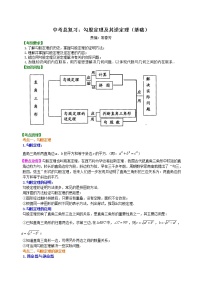
中考总复习：勾股定理及其逆定理-- 巩固练习（提高）

这是一份中考总复习：勾股定理及其逆定理-- 巩固练习（提高），共14页。

一、选择题
1．（2011湖北黄石）将一个有45度角的三角板的直角顶点C放在一张宽为3cm的纸带边沿上，另一个顶点A在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30度角，如图，则三角板的最大边的长为（ ）. A. 3cm B. 6cm C. 3cm D. 6cm
2．在△中，若，则△是（ ）.
. 锐角三角形 . 钝角三角形 . 等腰三角形 . 直角三角形
3. 如图，已知直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=DC=5，点P在BC上移动，则当PA+PD取最小值时，△APD中边AP上的高为（ ）.
A. B. C. D.3

4.如图，分别以直角的三边为直径向外作半圆．设直线左边阴影部分的面积为，右边阴影部分的面积和为，则（ ）.

A． B． C． D．无法确定
5.（2014春•临沭县期中）如图，是一长、宽都是3cm，高BC=9cm的长方体纸箱，BC上有一点P，PC=BC，一只蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是（ ）
A．6cmB．3cmC．10cmD．12cm
6.（2012•宁波）勾股定理是几何中的一个重要定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为（ ）.
A.90 B．100 C．110 D．121
二、填空题
7. 如图，在由12个边长都为1且有一个锐角是60°的小菱形组成的网格中，点P是其中的一个顶点，以点P为直角顶点作格点直角三角形（即顶点均在格点上的三角形），请你写出所有可能的直角三角形斜边的长________．

8. 如图，已知点F的坐标为(3，0)，点A、B分别是某函数图象与x轴，y轴的交点，点P是此图像上的一动点，设点P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5－x(0≤x≤5),则结论：①AF=2； ②BF=5； ③OA=5； ④OB=3中，正确结论的序号是______________.

9.（2014•达州）如图，折叠矩形纸片ABCD，使点B落在边AD上，折痕EF的两端分别在AB、BC上（含端点），且AB=6cm，BC=10cm．则折痕EF的最大值是 cm．
10.勾股定理有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理．在右图的勾股图中，已知∠ACB=90°，∠BAC=30°，AB=4．作△PQR使得∠R=90°，点H在边QR上，点D，E在边PR上，点G，F在边PQ上，那么△PQR的周长等于_________________.
11．观察下列一组数：
列举：3、4、5，猜想：32=4+5；
列举：5、12、13，猜想：52=12+13；
列举：7、24、25，猜想：72=24+25；…
列举：13、b、c，猜想：132=b+c；
请你分析上述数据的规律，结合相关知识求得b=_____,c=________.
12.如图，正方体的棱长为2，O为AD的中点，则O，A1，B三点为顶点的三角形面积为________________．
三、解答题
13. 作长为、、的线段.
14.如图A、B为两个村庄，AB、BC、CD为公路，BD为田地，AD为河宽，且CD与AD互相垂直。现要从点E处开设通往村庄A、村庄B的一条电缆，现在共有两种铺设方案：方案一：E→D→A→B；方案二：E→C→B→A．经测量得千米，BC=10千米，∠BDC=45°，∠ABD=15°．已知：地下电缆的修建费为2万元／千米，水下电缆的修建费为4万元／千米．
求：1)河宽AD(结果保留根号)；
2)公路CD的长;
3)哪种方案铺设电缆的费用低?请说明理由。


15. （2014春•朝阳区期末）如图，Rt△ABC中，∠ACB=90°，∠BAC=30°，AB=4，分别以AB、BC、AC为边作正方形ABED、BCFK、ACGH，再作Rt△PQR，使∠R=90°，点H在边QR上，点D、E在边PR上，点G、F在边PQ上，求PQ的长？
16．刘卫同学在一次课外活动中，用硬纸片做了两个直角三角形，见图①、②．图①中，∠B=90°，∠A=30°，BC=6cm；图②中，∠D=90°，∠E=45°，DE=4cm．图③是刘卫同学所做的一个实验：他将△DEF的直角边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动．在移动过程中，D、E两点始终在AC边上（移动开始时点D与点A重合）．
（1）在△DEF沿AC方向移动的过程中，刘卫同学发现：F、C两点间的距离逐渐________.．（填“不变”、“变大”或“变小”）
（2）刘卫同学经过进一步地研究，编制了如下问题：
问题①：当△DEF移动至什么位置，即AD的长为多少时，F、C的连线与AB平行？
问题②：当△DEF移动至什么位置，即AD的长为多少时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形？
问题③：在△DEF的移动过程中，是否存在某个位置，使得∠FCD=15°？如果存在，求出AD的长度；如果不存在，请说明理由．
请你分别完成上述三个问题的解答过程．

【答案与解析】
一．选择题
1.【答案】D.
【解析】过点A作AH垂直于纸带边沿于点H，
在直角△AHC中，∵AH=3，∠ACH=30°，
∴AC=2AH=6,
再在等腰直角△ABC中，∵AC=6, ∠B=45°，
∴AB=.
故选D.
2．【答案】D.
【解析】因为=4，所以，
，由勾股定理的逆定理可知：△ABC是直角三角形, 答案选D.
3．【答案】C．
【解析】如图，过D点作DE⊥BC于E,则DE=AB，AD=BE,EC=BC－BE=3
在Rt△CDE中，DE=,
延长AB至F，使AB=BF，连接DF，交BC于P点，连接AP，
这时候PA+PD取最小值，
∵AD∥BC，B是AF中点，
∴
在Rt△ABP中，AP=
∵
∴=,故选C.
4．【答案】A.
【解析】圆的面积为，设三条边长为a,b,c,分别表示三块阴影部分面积，用勾股定理即可.
5．【答案】A．
【解析】（1）如图1，AD=3cm，DP=3+6=9cm，在Rt△ADP中，AP==3cm；
（2）如图2，AC=6cm，CP=3+3=6cm，
Rt△ADP中，AP==6cm．
综上，蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是6cm．故选A．
6．【答案】 C.
二．填空题
7．【答案】2，，，4，.
【解析】如下图，可能的直角三角形斜边长有2，，，4，.

8．【答案】①； ②； ③ .
【解析】令x=0得到d=5,此时点P与点B重合，BF=5，由勾股定理的OB=4.令x=5得到d=2,此时点P与点A重合，可得AO=5，AF=2.
9．【答案】.
【解析】如图，点F与点C重合时，折痕EF最大，
由翻折的性质得，BC=B′C=10cm，
在Rt△B′DC中，B′D===8cm，
∴AB′=AD﹣B′D=10﹣8=2cm，
设BE=x，则B′E=BE=x，
AE=AB﹣BE=6﹣x，
在Rt△AB′E中，AE2+AB′2=B′E2，
即（6﹣x）2+22=x2，
解得x=，
在Rt△BEF中，EF===cm．
故答案为：．
10．【答案】27+13．
【解析】在直角△ABC中，根据三角函数即可求得AC，进而由等边三角形的性质和正方形的性质及三角函数就可求得QR的长，在直角△QRP中运用三角函数即可得到RP、QP的长，就可求出△PQR的周长．
11.【答案】 84,85.
【解析】认真观察三个数之间的关系：首先发现每一组的三个数为勾股数，第一个数为从3开始连续的奇数，第二、三个数为连续的自然数；进一步发现第一个数的平方是第二、三个数的和；最后得出第n组数为（2n+1），（），（），由此规律解决问题．
12．【答案】.
【解析】直角△AA1O和直角△OBA中，利用勾股定理可以得到OA1=OB=，
在直角△A1AB中，利用勾股定理得A1B=2，过点O作高，交A1B与M，连接AM，
则△AOM是直角三角形，则AM=A1B=，OM==，
∴△OA1B的面积=A1B•OM=．
三.综合题
13．【解析】
作法：如图所示

（1）作直角边为1（单位长度）的等腰直角△ACB，使AB为斜边；
（2）作以AB为一条直角边，另一直角边为1的Rt。斜边为；
（3）顺次这样做下去，最后做到直角三角形，这样斜边、、、的长 度就是、、、.
14．【解析】1).过B作BF⊥AD交DA延长线于F，
在Rt△ABF中，可知∠BAF=60°，AB，
∴ BF=6，，
在Rt△BFD中，∵∠BDF=45°，
∴ DF=BF=6，
∴
2).过B作BG⊥CD于G，则BG=6，BC=10，有CG=8，
∴ DC=CG+DG=14.
3).设CE=x，则方案一、二费用分别为：
，
，
由可解得
∴ 当＜CE＜14时，方案一较省；
当0＜CE＜时，方案二较省；
当CE=时，方案一、二均可．
15．【解析】
解：延长BA交QR于点M，连接AR，AP．
在△ABC和△GFC中
，
∴△ABC≌△GFC（SAS），
∴∠CGF=∠BAC=30°，
∴∠HGQ=60°，
∵∠HAC=∠BAD=90°，
∴∠BAC+∠DAH=180°，
又∵AD∥QR，
∴∠RHA+∠DAH=180°，
∴∠RHA=∠BAC=30°，
∴∠QHG=60°，
∴∠Q=∠QHG=∠QGH=60°，
∴△QHG是等边三角形．
AC=AB•cs30°=4×=2，
则QH=HA=HG=AC=2，
在直角△HMA中，HM=AH•sin60°=2×=3，AM=HA•cs60°=，
在直角△AMR中，MR=AD=AB=4．
∴QR=2+3+4=7+2，
∴QP=2QR=14+4．
故答案为：14+4．
16. 【解析】
（1）变小；
（2）问题①：∵∠B=90°，∠A=30°，BC=6cm
∴AC=12
∵∠FDE=90°，∠DEF=45°，DE=4
∴DF=4cm
连接FC，设FC∥AB
∴∠FCD=∠A=30°
∴在Rt△FDC中，DC=4
∴AD=AC-DC=12-4
∴AD=12-4时，FC∥AB；
问题②：设AD=x，在Rt△FDC中，FC2=DC2+FD2=（12-x）2+16
∵AC=12cm，DE=4cm，
∴AD≤8cm，
（I）当FC为斜边时，
由AD2+BC2=FC2得，x2+62=（12-x）2+16，x=；
（II）当AD为斜边时，
由FC2+BC2=AD2得，（12-x）2+16+62=x2，x=＞8（不合题意舍去）；
（III）当BC为斜边时，
由AD2+FC2=BC2得，x2+（12-x）2+16=36，x2-24x+160=0，
方程无解，
∴由（I）、（II）、（III）得，当x=时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形；
另解：BC不能为斜边，
∵FC＞CD，∴FC+AD＞12
∴FC、AD中至少有一条线段的长度大于6，
∴BC不能为斜边，
∴由（I）、（II）、（III）得，当x=cm时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形；
问题③：解法一：不存在这样的位置，使得∠FCD=15,°
理由如下：
假设∠FCD=15°
∵∠EFC=30°
作∠EFC的平分线，交AC于点P
则∠EFP=∠CFP=15°，∠DFE+∠EFP=60°
∴PD=4，PC=PF=2FD=8
∴PC+PD=8+4＞12
∴不存在这样的位置，使得∠FCD=15°;
解法二：不存在这样的位置，使得∠FCD=15°
假设∠FCE=15°AD=x
由∠FED=45°
得∠EFC=30°
作EH⊥FC，垂足为H．
∴HE=EF=2
CE=AC-AD-DE=8-x
且FC2=（12-x）2+16
∵∠FDC=∠EHC=90°
∠DCF为公共角
∴△CHE∽△CDF
∴=
又（）2=（）2=
∴（）2=，即=
整理后，得到方程x2-8x-32=0
∴x1=4-4＜0（不符合题意，舍去）
x2=4+4＞8（不符合题意，舍去）
∴不存在这样的位置，使得∠FCD=15°．