初中冀教版22.3 三角形的中位线优秀ppt课件

这是一份初中冀教版22.3 三角形的中位线优秀ppt课件，共16页。PPT课件主要包含了探究与思考，还有另外的证法吗，用符号语言表示，61°，巩固新知等内容，欢迎下载使用。

叫做三角形的中位线，一个三角形有 条中位线．
连接三角形两边中点的线段
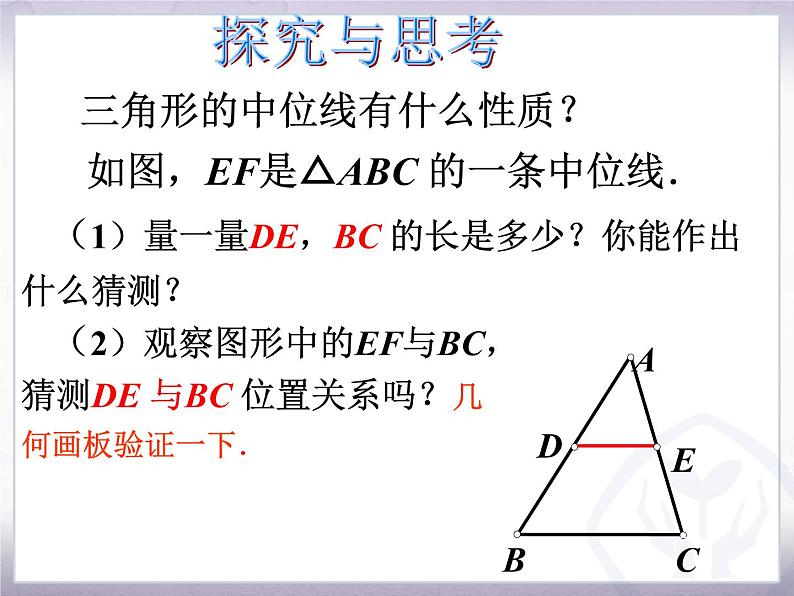
三角形的中位线有什么性质？
如图，EF是△ABC 的一条中位线．
（1）量一量DE，BC 的长是多少？你能作出什么猜测？
（2）观察图形中的EF与BC，猜测DE 与BC 位置关系吗？几何画板验证一下．
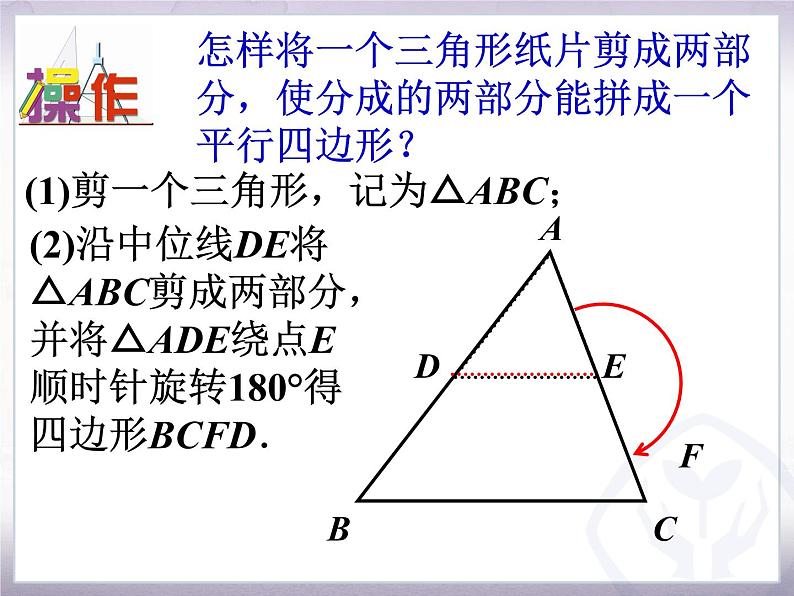
怎样将一个三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形？
(1)剪一个三角形，记为△ABC；
(2)沿中位线DE将△ABC剪成两部分，并将△ADE绕点E顺时针旋转180°得四边形BCFD．
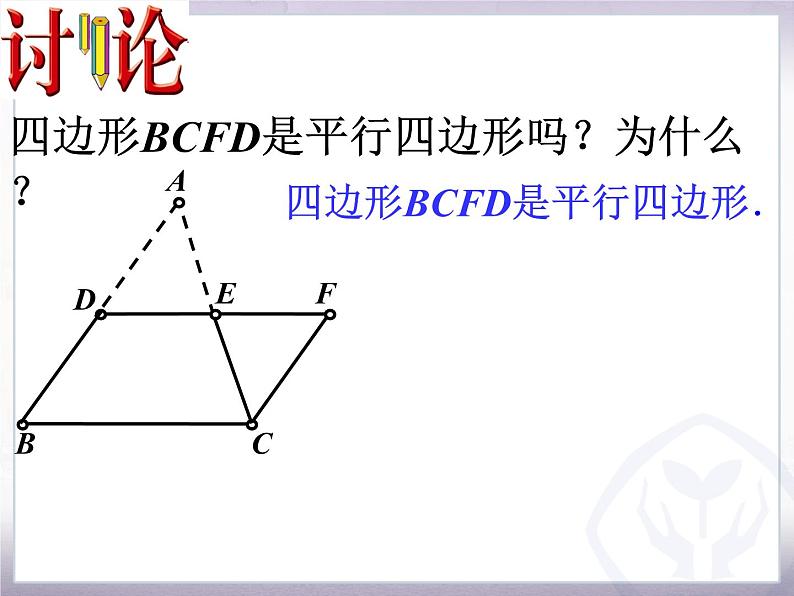
四边形BCFD是平行四边形吗？为什么？
四边形BCFD是平行四边形．
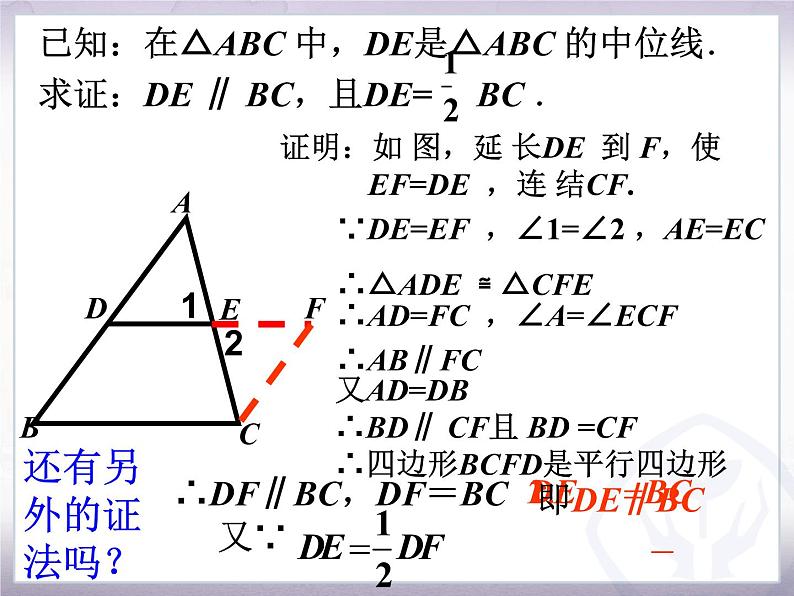
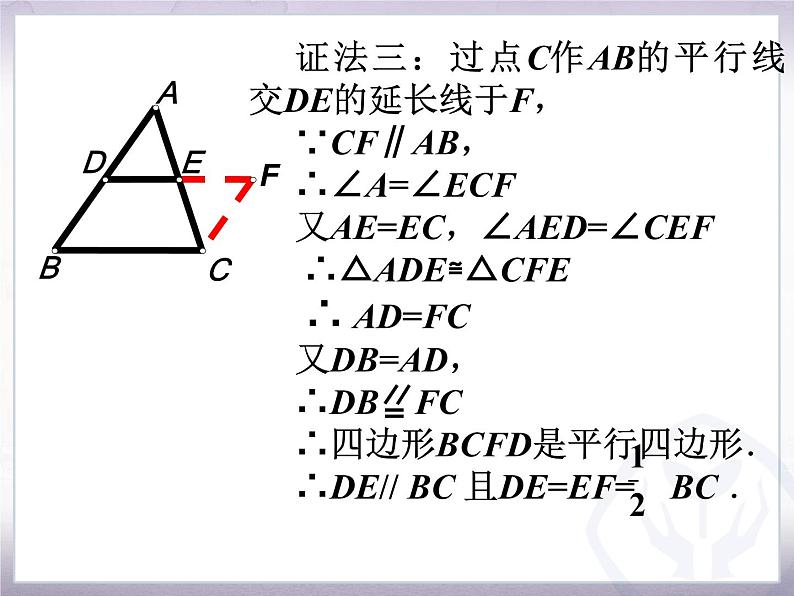
∵DE=EF ，∠1=∠2 ，AE=EC∴△ADE ≌ △CFE
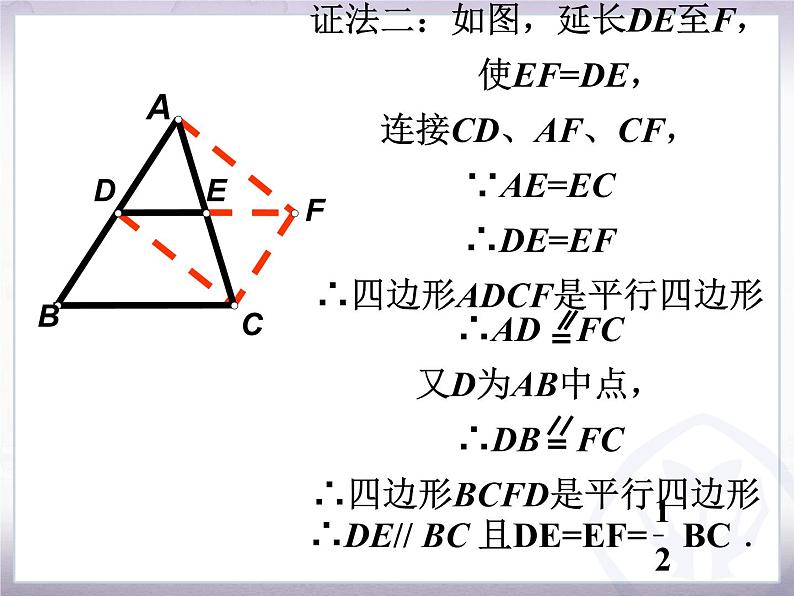
证明：如 图，延 长DE 到 F，使EF=DE ，连 结CF.
∴AD=FC ，∠A=∠ECF∴AB∥FC
又AD=DB ∴BD∥ CF且 BD =CF∴四边形BCFD是平行四边形
∴DF∥BC，DF＝BC
三角形中位线定理三角形的中位线平行于第三边，且等于第三边的一半．
∵DE是△ABC的中位线∴ DE∥BC，
(1)证明平行； (2)证明一条线段是另一条线段的2倍或 ．
三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．
三角形的中位线定理的主要用途：
例 已知：如图22-3-6，在四边形ABCD中，AD=BC，P为对角线BD的中点，M为DC的中点，N为AB的中点．求证：△PMN是等腰三角形．
证明：在△ABD中，∵N，P分别为AB,BD的中点，∴NP= AD.同理 PM= BC.又∵AD=BC，∴PN=PM.∴△PMN是等腰三角形．
1、如图，MN 为△ABC 的中位线，若∠ABC =61°，则∠AMN = ，若MN =12 ，则BC = .
2、如图， △ABC 中， D ，E 分别为AB，AC 的中点，当BC =10㎝时，则DE = .
3、如图，已知△ABC中，AB = 3㎝，BC=3.4㎝，AC=4㎝且D，E，F分别为 AB，BC，AC边的中点，则△DEF的周长是 ㎝.
4、如下图：在Rt △ ABC中，∠A=90°，D、E、F分别是各边中点， AB=6cm，AC=8cm，则△DEF的周长= cm ．