





初中冀教版第十二章 分式和分式方程12.1 分式课堂教学ppt课件
展开分式的定义分式有(无)意义及分式值为零的条件分式的基本性质
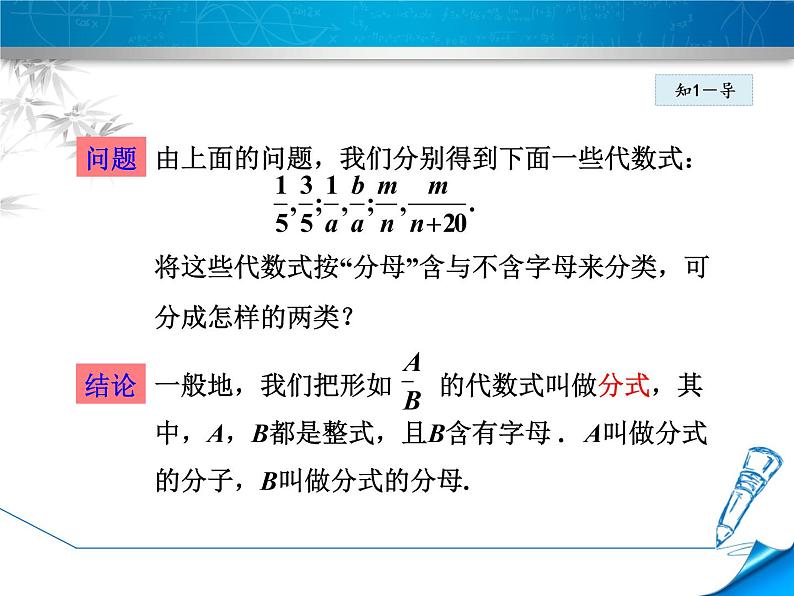
为了调查珍稀动物资源,动物专家在p平方千米的保护区找到7只灰熊.你能用代数式表示该保护区平均每平方千米内有多少只灰熊吗?
1.一项工程,甲施工队5天可以完成.甲施工队每天完成的工程量是多少? 3天完成的工程量又是多少?如果乙施工队a天可以完成这项工程,那么乙施工队每天完成的工程量是多少? b(b
一般地,我们把形如 的代数式叫做分式,其中,A,B都是整式,且B含有字母 . A叫做分式的分子,B叫做分式的分母.
(1)分式与分数的相同点是:形式相同,都有分子和分母;不同点是:分式的分母含有字母. (2)分式与整式的不同点是:整式的分母不含有字母;分式的分母含有字母.
因为 的分母都含有字母,所以它们都是分式.
指出下列各式中,哪些是整式,哪些是分式.
分式只注重形式而不注重结果,判断一个式子是不是分式的方法:首先要具有 的形式,其次A,B都是整式,最后看B是不是含有字母.分母含有字母是判断分式的关键条件.
下列各式中,哪些是分式?哪些是整式? -3a2,
2 设A,B都是整式,若 表示分式,则( ) A.A,B中都必须含有字母 B.A中必须含有字母 C.B中必须含有字母 D.A,B中都不含字母3 下列各式中,是分式的是( ) A. B. C. D. x2y+4
分式有(无)意义及分式值为零的条件
分式 的分母中的字母a能取任何实数吗?为什么?分式 中的字母x呢?
在分数中,分母不能等于0.同样,在分式中,分母也不能等于0,即当分式的分母等于0时,分式没有意义.如 分式,当x-5≠0,即x≠5时,它有意义;当x-5=0,即x=5时,它没有意义.
1.在分式中,当分母不为0时,分式有意义; 当分母为0时,分式无意义.2.分式的值为零的条件:分子为零,分母不为零.
例2 [中考·常州]要使分式 有意义,则x的取 值范围是( ) A.x>-3 B.x<-3 C.x≠-3 D.x≠0
导引: 直接根据分式有意义的条件确定x的取值范围. 由于x+3是分式的分母,因此x+3≠0. 所以x≠-3.
求分式有意义时字母的取值范围,一般是根据分母不等于0构造不等式,求使分式的分母不等于零的字母的取值范围,与分子的取值无关.
在什么情况下,下列各分式无意义?
2 使分式 无意义的x满足的条件是( ) A.x=2 B.x=-2 C.x≠2 D.x≠-23 下列各式中,无论x取何值,分式都有意义的 是( ) A. B. C. D.
例3 [中考·毕节] 若分式 的值为零,则x的值 为( ) A.0 B.1 C.-1 D.±1
导引:分式的值为零的条件是分子为0,分母不为0. 由此条件解出x即可. 由x2-1=0,得 x = ±1 . 当x=1时,x-1=0, 故x=1不合题意;当x=-1时,x-1=-2≠0, 所以x=-1时分式的值为零.
分式的值为零必须同时满足两个条件:分子为零且分母不为零,两者缺一不可.
【中考·温州】若分式 的值为0,则x的 值是( ) A.-3 B.-2 C.0 D.22 当分式 的值为0时,x的值是( ) A.0 B.1 C.-1 D.-2
分数的分子和分母同乘(或除以)一个不等于0的整式,分式的值不变.如
类比分数的这种性质,思考:分式的分子和分母同乘(或除以)一个不等于0的整式,分式的值会怎样?
分式的分子和分母同乘(或除以)一个不等于0的整式,分式的值不变.其中,M是不等于0的整式.
例4 下列等式的右边是怎样从左边得到的?
导引:(1) 等号左边的分子、分母没有出现c,右边有c, 说明分式的分子、分母同乘c;(2)等号左边的分 式中分子、分母都含有x,题中隐含x≠0 ,而右 边分母不含有x,说明分式的分子、分母同除以x. 解:(1)分子、分母同乘c. (2)分子、分母同除以x.
应用分式的基本性质时,一定要确定分式在有意义的情况下才能应用.应用时要注意是否符合两个“ 同”:一是要同时进行“ 乘法”或“ 除法”运算;二是“ 乘(或除以)”的对象必须是同一个不等于0的整式.
如果把 中的x与y都扩大到原来的20倍, 那么这个式子的值( ) A.不变 B.扩大到原来的10倍 C.扩大到原来的20倍 D.缩小到原来的
2 写出下列等式中所缺的分子或分母. (1) (c≠0); (2) (a≠-b); (3)3 下列式子从左到右的变形一定正确的是( ) A. B. C. D.
初中数学冀教版八年级上册12.1 分式作业ppt课件: 这是一份初中数学冀教版八年级上册12.1 分式作业ppt课件,共21页。
分式及其基本性质PPT课件免费下载: 沪科版初中数学七年级下册课文《分式及其基本性质》,完整版PPT课件免费下载,优秀PPT背景图搭配,精美的免费ppt模板。轻松备课,欢迎免费下载使用。
沪科版八年级上册第12章 一次函数12.1 函数优秀课件ppt: 这是一份沪科版八年级上册第12章 一次函数12.1 函数优秀课件ppt,共20页。PPT课件主要包含了答案显示,单价数量金额,见习题等内容,欢迎下载使用。













