2020版高考新创新一轮复习数学（理）通用版讲义：第五章第一节　平面向量的概念及线性运算

第五章 平面向量
第一节　平面向量的概念及线性运算
[考纲要求]
1．了解向量的实际背景．
2．理解平面向量的概念，理解两个向量相等的含义．
3．理解向量的几何表示．
4．掌握向量加法、减法的运算，并理解其几何意义．
5．掌握向量数乘的运算及其几何意义，理解两个向量共线的含义．了解向量线性运算的性质及其几何意义．　　　
突破点一　平面向量的有关概念


名称
定义
备注
向量
既有大小又有方向的量叫做向量；向量的大小叫做向量的长度(或称模)
平面向量是自由向量，平面向量可自由平移
零向量
长度为0的向量；其方向是任意的
记作0
单位向量
长度等于1个单位的向量
非零向量a的单位向量为±
平行向量
方向相同或相反的非零向量，又叫做共线向量
0与任一向量平行或共线
相等向量
长度相等且方向相同的向量
两向量只有相等或不等，不能比较大小
相反向量
长度相等且方向相反的向量
0的相反向量为0

一、判断题(对的打“√”，错的打“×”)
(1)向量与有向线段是一样的，因此可以用有向线段来表示向量．(　　)
(2)若a与b不相等，则a与b一定不可能都是零向量．(　　)
答案：(1)×　(2)√
二、填空题
1．如果对于任意的向量a，均有a∥b，则b为________．
答案：零向量
2．若e是a的单位向量，则a与e的方向________．
解析：∵e＝，∴e与a的方向相同．
答案：相同
3．△ABC中，点D，E，F分别为BC，CA，AB的中点，在以A，B，C，D，E，F为端点的有向线段所表示的向量中，与共线的向量有________个．
答案：7个


1．(2018·海淀期末)下列说法正确的是(　　)
A．方向相同的向量叫做相等向量
B．共线向量是在同一条直线上的向量
C．零向量的长度等于0
D．∥就是所在的直线平行于所在的直线
解析：选C　长度相等且方向相同的向量叫做相等向量，故A不正确；方向相同或相反的非零向量叫做共线向量，但共线向量不一定在同一条直线上，故B不正确；显然C正确；当∥时，所在的直线与所在的直线可能重合，故D不正确．
2．(2019·辽宁实验中学月考)有下列命题：
①若|a|＝|b|，则a＝b；
②若||＝||，则四边形ABCD是平行四边形；
③若m＝n，n＝k，则m＝k；
④若a∥b，b∥c，则a∥c.
其中，假命题的个数是(　　)
A．1　　　　　　　　　 B．2
C．3 D．4
解析：选C　对于①，|a|＝|b|，a，b的方向不确定，则a，b不一定相等，所以①错误；对于②，若||＝||，则，的方向不一定相同，所以四边形ABCD不一定是平行四边形，②错误；对于③，若m＝n，n＝k，则m＝k，③正确；对于④，若a∥b，b∥c，则b＝0时，a∥c不一定成立，所以④错误．综上，假命题的是①②④，共3个，故选C.
3．(2019·赣州崇义中学模拟)向量与共线是A，B，C，D四点共线的(　　)
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
解析：选B　由A，B，C，D四点共线，得向量与共线，反之不成立，可能AB∥CD，所以向量与共线是A，B，C，D四点共线的必要不充分条件，故选B.

关于平面向量的3个易错提醒
(1)两个向量不能比较大小，只可以判断它们是否相等，但它们的模可以比较大小；
(2)大小与方向是向量的两个要素，分别是向量的代数特征与几何特征；
(3)向量可以自由平移，任意一组平行向量都可以移到同一直线上．
突破点二　平面向量的线性运算


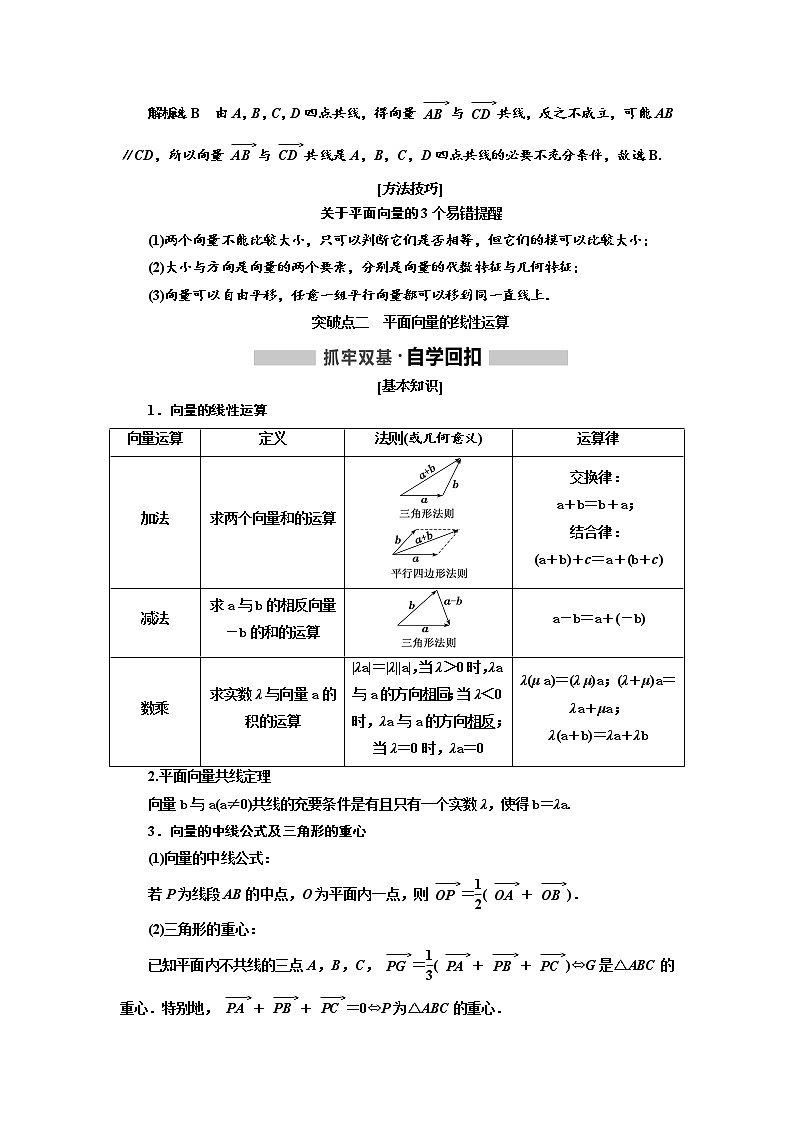
1．向量的线性运算
向量运算
定义
法则(或几何意义)
运算律
加法
求两个向量和的运算


交换律：
a＋b＝b＋a；
结合律：
(a＋b)＋c＝a＋(b＋c)
减法
求a与b的相反向量－b的和的运算

a－b＝a＋(－b)
数乘
求实数λ与向量a的积的运算
|λa|＝|λ||a|，当λ＞0时，λa与a的方向相同；当λ＜0时，λa与a的方向相反；当λ＝0时，λa＝0
λ(μ a)＝(λ μ)a；(λ＋μ)a＝λa＋μa；
λ(a＋b)＝λa＋λb
2.平面向量共线定理
向量b与a(a≠0)共线的充要条件是有且只有一个实数λ，使得b＝λa.
3．向量的中线公式及三角形的重心
(1)向量的中线公式：
若P为线段AB的中点，O为平面内一点，则＝(＋)．
(2)三角形的重心：
已知平面内不共线的三点A，B，C，＝(＋＋)⇔G是△ABC的重心．特别地，＋＋＝0⇔P为△ABC的重心．

一、判断题(对的打“√”，错的打“×”)
(1)a∥b是a＝λb(λ∈R)的充要条件．(　　)
(2)△ABC中，D是BC的中点，则＝(＋)．(　　)
答案：(1)×　(2)√
二、填空题
1．在如图所示的方格纸中有定点O，P，Q，E，F，G，H，则＋＝________.

答案：
2．化简：(－)－(－)＝________.
解析：(－)－(－)＝－－＋＝(－)＋(－)＝＋＝0.
答案：0
3．已知向量a，b不共线，且c＝λa＋b，d＝a＋(2λ－1)b，若c与d共线反向，则实数λ的值为________．
答案：－


考法一　平面向量的线性运算　
应用平面向量的加法、减法和数乘运算的法则即可．
(1)加法的三角形法则要求“首尾相接”，加法的平行四边形法则要求“起点相同”；
(2)减法的三角形法则要求“起点相同”且差向量指向“被减向量”；
(3)数乘运算的结果仍是一个向量，运算过程可类比实数运算．
[例1]　(1)(2019·湖北咸宁联考)如图，在△ABC中，点M为AC的中点，点N在AB上，＝3，点P在MN上，＝2，那么＝(　　)
A.－　　　　 B.－
C.－ D.＋
(2)如图，在直角梯形ABCD中，＝，＝2，且＝r＋s，则2r＋3s＝(　　)
A．1 B．2
C．3 D．4
[解析]　(1)＝＋＝＋＝＋(－)＝＋＝＋.故选D.
(2)根据图形，由题意可得＝＋＝＋＝＋(＋＋)＝＋(＋)＝＋＝＋.
因为＝r＋s，所以r＝，s＝，则2r＋3s＝1＋2＝3.
[答案]　(1)D　(2)C
[方法技巧]
1．平面向量的线性运算技巧
(1)不含图形的情况：可直接运用相应运算法则求解．
(2)含图形的情况：将它们转化到三角形或平行四边形中，充分利用相等向量、相反向量、三角形的中位线等性质，把未知向量用已知向量表示出来求解．
2．利用平面向量的线性运算求参数的一般思路
(1)没有图形的准确作出图形，确定每一个点的位置．
(2)利用平行四边形法则或三角形法则进行转化，转化为要求的向量形式．
(3)比较、观察可知所求．　　


考法二　平面向量共线定理的应用　
求解向量共线问题的注意事项
(1)向量共线的充要条件中，当两向量共线时，通常只有非零向量才能表示与之共线的其他向量，注意待定系数法和方程思想的运用．
(2)证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得到三点共线．
(3)直线的向量式参数方程：A，P，B三点共线⇔＝(1－t)·＋t (O为平面内任一点，t∈R)．
[例2]　(1)(2019·南昌莲塘一中质检)已知a，b是不共线的向量，＝λa＋b，＝a＋μb(λ，μ∈R)，若A，B，C三点共线，则λ，μ的关系一定成立的是(　　)
A．λμ＝1 B．λμ＝－1
C．λ－μ＝－1 D．λ＋μ＝2
(2)(2019·郑州模拟)设e1与e2是两个不共线向量，＝3e1＋2e2，＝ke1＋e2，＝3e1－2ke2，若A，B，D三点共线，则k的值为________．
[解析]　(1)∵与有公共点A，∴若A，B，C三点共线，则存在一个实数t使＝t，即λa＋b＝ta＋μtb，则消去参数t得λμ＝1；反之，当λμ＝1时，＝a＋b，此时存在实数使＝，故和共线．∵与有公共点A，∴A，B，C三点共线．故选A.
(2)由题意，A，B，D三点共线，故必存在一个实数λ，使得＝λ.
又＝3e1＋2e2，＝ke1＋e2，＝3e1－2ke2，
所以＝－＝3e1－2ke2－(ke1＋e2)
＝(3－k)e1－(2k＋1)e2，
所以3e1＋2e2＝λ(3－k)e1－λ(2k＋1)e2，
又e1与e2不共线，
所以解得k＝－.
[答案]　(1)A　(2)－
[方法技巧]　　平面向量共线定理的3个应用
证明向量共线
对于非零向量a，b，若存在实数λ，使a＝λb，则a与b共线
证明三点共线
若存在实数λ，使＝λ，与有公共点A，则A，B，C三点共线
求参数的值
利用向量共线定理及向量相等的条件列方程(组)求参数的值

1.在等腰梯形ABCD中，＝－2，M为BC的中点，则＝(　　)
A.＋ B.＋
C.＋ D.＋
解析：选B　因为＝－2，所以＝2.又M是BC的中点，所以＝(＋)＝(＋＋)＝＝＋，故选B.
2.在△ABC中，AB＝2，BC＝3，∠ABC＝60°，AD为BC边上的高，O为AD的中点，若＝λ＋μ，其中λ，μ∈R，则λ＋μ等于(　　)
A．1 B.
C. D.
解析：选D　由题意易得＝＋＝＋，
则2＝＋，即＝＋.
故λ＋μ＝＋＝.
3.设两个非零向量a与b不共线．
(1)若＝a＋b，＝2a＋8b，＝3(a－b)，求证：A，B，D三点共线；
(2)试确定实数k，使ka＋b和a＋kb共线．
解：(1)证明：∵＝a＋b，＝2a＋8b，＝3(a－b)，
∴＝＋＝2a＋8b＋3(a－b)＝5(a＋b)＝5，
∴，共线，又它们有公共点B，
∴A，B，D三点共线．
(2)∵ka＋b与a＋kb共线，
∴存在实数λ，使ka＋b＝λ(a＋kb)，即(k－λ)a＝(λk－1)b.
又a，b是两个不共线的非零向量，
∴∴k2－1＝0.∴k＝±1.
[课时跟踪检测]
1．(2019·山东省实验中学高三摸底测试)已知a，b是两个非零向量，且|a＋b|＝|a|＋|b|，则下列说法正确的是(　　)
A．a＋b＝0　　　　　　　 B．a＝b
C．a与b反向共线 D．存在正实数λ，使得a＝λb
解析：选D　由已知得，向量a与b为同向向量，即存在正实数λ，使得a＝λb，故选D.
2．设a0为单位向量，下述命题中：①若a为平面内的某个向量，则a＝|a|a0；②若a与a0平行，则a＝|a|a0；③若a与a0平行且|a|＝1，则a＝a0.假命题的个数是(　　)
A．0 B．1
C．2 D．3
解析：选D　向量是既有大小又有方向的量，a与|a|a0的模相同，但方向不一定相同，故①是假命题；若a与a0平行，则a与a0的方向有两种情况：一是同向，二是反向，反向时a＝－|a|a0，故②③也是假命题．综上所述，假命题的个数是3.
3．(2019·广东仲元中学期中)在平行四边形ABCD中，下列结论错误的是(　　)
A．||＝||一定成立 B．＝＋一定成立
C．＝一定成立 D．＝－一定成立
解析：选A　在平行四边形ABCD中，＝＋一定成立，＝一定成立，＝－一定成立，但||＝||不一定成立．故选A.

4．(2019·石家庄高三一检)在△ABC中，点D在边AB上，且＝，设＝a，＝b，则＝(　　)
A.a＋b B.a＋b
C.a＋b D.a＋b
解析：选B　∵＝，∴＝，∴＝＋＝＋＝＋(－)＝＋＝a＋b，故选B.
5.(2019·长春模拟)如图所示，下列结论正确的是(　　)

①＝a＋b；
②＝a－b；
③＝a－b；
④＝a＋b.
A．①② B．③④
C．①③ D．②④
解析：选C　①根据向量的加法法则，得＝a＋b，故①正确；②根据向量的减法法则，得＝a－b，故②错误；③＝＋＝a＋b－2b＝a－b，故③正确；④＝＋＝a＋b－b＝a＋b，故④错误，故选C.
6．(2019·嘉兴调研)已知点O为△ABC外接圆的圆心，且＋＋＝0，则△ABC的内角A等于(　　)
A．30° B．45°
C．60° D．90°
解析：选A　由＋＋＝0得，＋＝，由O为△ABC外接圆的圆心，结合向量加法的几何意义知，四边形OACB为菱形，且∠CAO＝60°，故A＝30°.
7.(2019·江西新余第一中学模拟)如图，已知△OAB，若点C满足＝2，＝λ＋μ (λ，μ∈R)，则＋＝(　　)
A. B.
C. D.
解析：选D　∵＝＋＝＋＝＋(－)＝＋，∴λ＝，μ＝，∴＋＝3＋＝.故选D.
8．(2019·张家口月考)在四边形ABCD中，对角线AC与BD交于点O，若2＋＝2＋，则四边形ABCD一定是(　　)
A．矩形 B．梯形
C．平行四边形 D．菱形
解析：选B　∵2＋＝2＋，∴2(－)＝－，即2＝，∴DA∥CB，且2| |＝||，∴四边形ABCD一定是梯形．故选B.
9．(2019·甘肃诊断)设D为△ABC所在平面内一点，＝－4，则＝(　　)
A.－ B.＋
C.－ D.＋
解析：选B　法一：设＝x＋y，由＝－4可得，＋＝－4－4，即－－3＝－4x－4y，则解得即＝ ＋，故选B.
法二：在△ABC中，＝－4，即－＝，则＝＋＝－＝－(＋)＝＋，故选B.

10.(2019·曲阜模拟)如图，在△ABC中，＝，P是BN上的一点，若＝m＋，则实数m的值为(　　)
A. B.
C．1 D．3
解析：选B　因为＝，所以＝4.所以＝m＋＝m＋，因为B，P，N共线，所以m＋＝1，m＝.
11．(2019·河南三市联考)若＝，＝(λ＋1)，则λ＝________.
解析：由＝可知，点P是线段AB上靠近点A的三等分点，则＝－，所以λ＋1＝－，解得λ＝－.
答案：－
12．(2019·石家庄高三摸底考试)平行四边形ABCD中，M为BC的中点，若＝λ＋μ，则λμ＝________.
解析：∵＝－＝－＝－2＝3－2，∴＝λ＋3μ－2μ，∴(1－3μ)＝(λ－2μ)，∵和是不共线向量，∴解得∴λμ＝.
答案：
13．(2019·盐城一模)在△ABC中，∠A＝60°，∠A的平分线交BC于点D，若AB＝4，且＝＋λ (λ∈R)，则AD的长为________．
解析：因为B，D，C三点共线，所以＋λ＝1，解得λ＝，如图，过点D分别作AC，AB的平行线交AB，AC于点M，N，则＝，＝，经计算得AN＝AM＝3，AD＝3.
答案：3
14．在直角梯形ABCD中，∠A＝90°，∠B＝30°，AB＝2，BC＝2，点E在线段CD上，若＝＋μ，则μ的取值范围是________．
解析：由题意可求得AD＝1，CD＝，所以＝2.
∵点E在线段CD上，∴＝λ (0≤λ≤1)．
∵＝＋，
又＝＋μ＝＋2μ＝＋，
∴＝1，即μ＝.∵0≤λ≤1，∴0≤μ≤，
即μ的取值范围是.
答案：
15．已知O，A，B是不共线的三点，且＝m＋n (m，n∈R)．
(1)若m＋n＝1，求证：A，P，B三点共线；
(2)若A，P，B三点共线，求证：m＋n＝1.
证明：(1)若m＋n＝1，
则＝m ＋(1－m)
＝＋m (－)，
∴－＝m (－)，
即＝m ，∴与共线．
又∵与有公共点B，
∴A，P，B三点共线．
(2)若A，P，B三点共线，
则存在实数λ，使＝λ，
∴－＝λ(－)．
又＝m ＋n .
故有m ＋(n－1)＝λ－λ，
即(m－λ)＋(n＋λ－1)＝0.
∵O，A，B不共线，∴，不共线，
∴∴m＋n＝1.