2020版新一线高考理科数学一轮复习教学案：第2章第2节　函数的单调性与最值


第二节　函数的单调性与最值
[考纲传真]　1.理解函数的单调性、最大(小)值及其几何意义.2.会运用基本初等函数的图象分析函数的性质．

(对应学生用书第11页)
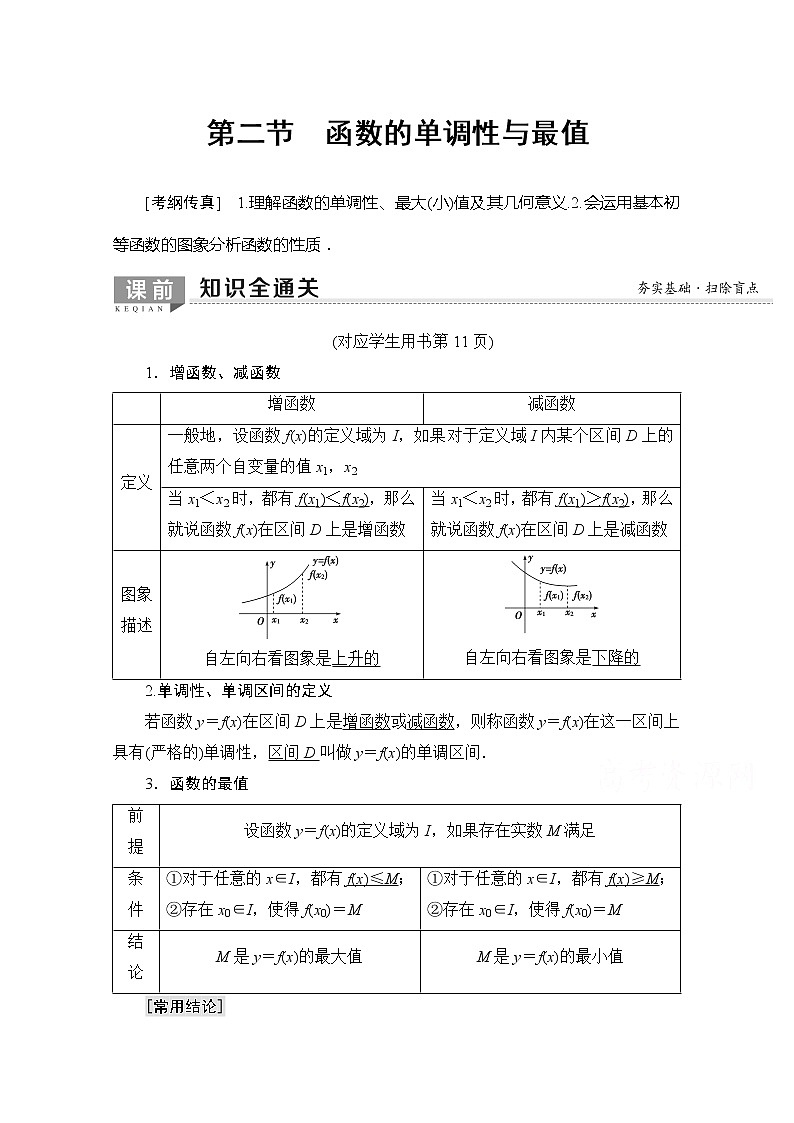
1．增函数、减函数

增函数
减函数
定义
一般地，设函数f(x)的定义域为I，如果对于定义域I内某个区间D上的任意两个自变量的值x1，x2
当x1＜x2时，都有f(x1)＜f(x2)，那么就说函数f(x)在区间D上是增函数
当x1＜x2时，都有f(x1)＞f(x2)，那么就说函数f(x)在区间D上是减函数
图象描述

自左向右看图象是上升的

自左向右看图象是下降的
2.单调性、单调区间的定义
若函数y＝f(x)在区间D上是增函数或减函数，则称函数y＝f(x)在这一区间上具有(严格的)单调性，区间D叫做y＝f(x)的单调区间．
3．函数的最值
前提
设函数y＝f(x)的定义域为I，如果存在实数M满足
条件
①对于任意的x∈I，都有f(x)≤M；
②存在x0∈I，使得f(x0)＝M
①对于任意的x∈I，都有f(x)≥M；
②存在x0∈I，使得f(x0)＝M
结论
M是y＝f(x)的最大值
M是y＝f(x)的最小值

函数单调性的常用结论
(1)对∀x1，x2∈D(x1≠x2)，＞0⇔f(x)在D上是增函数，＜0⇔f(x)在D上是减函数．
(2)对勾函数y＝x＋(a＞0)的增区间为(－∞，－]和[，＋∞)，减区间为[－，0)和(0，]．
(3)在区间D上，两个增函数的和仍是增函数，两个减函数的和仍是减函数．
(4)函数f(g(x))的单调性与函数y＝f(u)和u＝g(x)的单调性的关系是“同增异减”．
[基础自测]
1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)
(1)对于函数f(x)，x∈D，若对任意x1，x2∈D，x1≠x2且(x1－x2)·[f(x1)－f(x2)]>0，则函数f(x)在区间D上是增函数． ( )
(2)函数y＝的单调递减区间是(－∞，0)∪(0，＋∞)． ( )
(3)函数y＝|x|是R上的增函数． ( )
(4)函数y＝x2－2x在区间[3，＋∞)上是增函数，则函数y＝x2－2x的单调递增区间为[3，＋∞)． ( )
[答案]　(1)√　(2)×　(3)×　(4)×
2．(教材改编)如图是函数y＝f(x)，x∈[－4,3]上的图象，则下列说法正确的是( )

A．f(x)在[－4，－1]上是减函数，在[－1,3]上是增函数
B．f(x)在区间(－1,3)上的最大值为3，最小值为－2
C．f(x)在[－4,1]上有最小值－2，有最大值3
D．当直线y＝t与y＝f(x)的图象有三个交点时－1＜t＜2
C　[由图象知，函数f(x)在[－4,1]上有最小值－2，最大值3，故选C.]
3．(教材改编)已知函数f(x)＝，x∈[2,6]，则f(x)的最大值为________，最小值为________．
2　　[可判断函数f(x)＝在[2,6]上为减函数，所以f(x)max＝f(2)＝2，f(x)min＝f(6)＝.]
4．函数y＝(2k＋1)x＋b在R上是减函数，则k的取值范围是________．
　[由题意知2k＋1＜0，得k＜－.]
5．f(x)＝x2－2x，x∈[－2,3]的单调增区间为________，f(x)max＝________.
[1,3]　8　[f(x)＝(x－1)2－1，故f(x)的单调增区间为[1,3]，f(x)max＝f(－2)＝8.]

(对应学生用书第12页)

确定函数的单调性(区间)
【例1】　(1)(2017·全国卷Ⅱ)函数f(x)＝ln(x2－2x－8)的单调递增区间是( )
A．(－∞，－2) B．(－∞，1)
C．(1，＋∞) D．(4，＋∞)
D　[由x2－2x－8>0，得x>4或x<－2.
设t＝x2－2x－8，则y＝ln t在t∈(0，＋∞)上为增函数．
欲求函数f(x)的单调递增区间，即求函数t＝x2－2x－8的单调递增区间．
∵函数t＝x2－2x－8的单调递增区间为(4，＋∞)，
∴函数f(x)的单调递增区间为(4，＋∞)．
故选D.]
(2)试讨论函数f(x)＝x＋(k＞0)的单调性．
[解]　法一：由解析式可知，函数的定义域是(－∞，0)∪(0，＋∞)．在(0，＋∞)内任取x1，x2，令0＜x1＜x2，那么f(x2)－f(x1)＝－＝(x2－x1)＋k＝(x2－x1)·.
因为0＜x1＜x2，所以x2－x1＞0，x1x2＞0.
故当x1，x2∈(，＋∞)时，f(x1)＜f(x2)，
即函数在(，＋∞)上单调递增．
当x1，x2∈(0，)时，f(x1)＞f(x2)，
即函数在(0，)上单调递减．
考虑到函数f(x)＝x＋(k＞0)是奇函数，在关于原点对称的区间上具有相同的单调性，故在(－∞，－)上单调递增，在(－，0)上单调递减．
综上，函数f(x)在(－∞，－)和(，＋∞)上单调递增，在(－，0)和(0，)上单调递减．
法二：f′(x)＝1－.
令f′(x)＞0得x2＞k，即x∈(－∞，－)或x∈(，＋∞)，故函数的单调增区间为(－∞，－)和(，＋∞)．
令f′(x)＜0得x2＜k，即x∈(－，0)或x∈(0，)，故函数的单调减区间为(－，0)和(0，)．
故函数f(x)在(－∞，－)和(，＋∞)上单调递增，在(－，0)和(0，)上单调递减．
[规律方法]　1.确定函数单调性的4种方法
(1)定义法．利用定义判断．
(2)导数法．适用于可以求导的函数．
(3)图象法．由图象确定函数的单调区间需注意两点：一是单调区间必须是函数定义域的子集；二是图象不连续的单调区间要分开写，用“和”或“，”连接，不能用“∪”连接．
(4)复合函数法．对于函数y＝f(g(x))，先确定y＝f(v)，v＝g(x)的单调性，再利用“同增异减”的原则确定y＝f(g(x))的单调性．
易错警示：确定函数的单调性(区间)，应先求定义域，在定义域内确定单调性(区间)．
2．熟记函数单调性的4个常用结论
(1)若f(x)，g(x)均是区间A上的增(减)函数，则f(x)＋g(x)也是区间A上的增(减)函数；
(2)若k＞0，则kf(x)与f(x)单调性相同；若k＜0，则kf(x)与f(x)单调性相反；
(3)函数y＝f(x)(f(x)＞0)在公共定义域内与y＝－f(x)，y＝的单调性相反；
(4)函数y＝f(x)(f(x)≥0)在公共定义域内与y＝的单调性相同．
(1)已知函数f(x)＝，则该函数的单调递增区间为( )
A．(－∞，1] B．[3，＋∞)
C．(－∞，－1] D．[1，＋∞)
(2)(2019·郑州模拟)函数y＝的单调递增区间为( )
A．(1，＋∞) B.
C. D.
(1)B　(2)B　[(1)设t＝x2－2x－3，由t≥0，即x2－2x－3≥0，解得x≤－1或x≥3.
所以函数的定义域为(－∞，－1]∪[3，＋∞)．
因为函数t＝x2－2x－3的图象的对称轴为x＝1，
所以函数t在(－∞，－1]上单调递减，在[3，＋∞)上单调递增．
所以函数f(x)的单调递增区间为[3，＋∞)．
(2)令t＝2x2－3x＋1，则t＝2－.
又函数y＝是减函数，因此函数y＝的单调递增区间为.故选B.]
(3)试讨论函数f(x)＝(a≠0)在(－1,1)上的单调性．
[解]　法一：设－1＜x1＜x2＜1，
f(x)＝a＝a，
f(x1)－f(x2)＝a－a
＝，
由于－1＜x1＜x2＜1，
所以x2－x1＞0，x1－1＜0，x2－1＜0，
故当a＞0时，f(x1)－f(x2)＞0，
即f(x1)＞f(x2)，
函数f(x)在(－1,1)上递减；
当a＜0时，f(x1)－f(x2)＜0，即f(x1)＜f(x2)，
函数f(x)在(－1,1)上递增．
法二：f′(x)＝＝，
所以当a＞0时，f′(x)＜0，当a＜0时，f′(x)＞0，
即当a＞0时，f(x)在(－1,1)上为单调减函数，
当a＜0时，f(x)在(－1,1)上为单调增函数．

利用函数的单调性求最值(值域)
1．函数f(x)＝－log2(x＋2)在区间[－1,1]上的最大值为________．
3　[函数f(x)在区间[－1,1]上是减函数，则f(x)max＝f(－1)＝－log21＝3.]
2．函数f(x)＝，x∈[－5，－3]的值域为________．
　[f(x)＝＝＝3－，
则函数f(x)在区间[－5，－3]上是增函数．
所以f(x)max＝f(－3)＝3－＝10，
f(x)min＝f(－5)＝3－＝.
因此函数f(x)的值域为.]
3．函数f(x)＝的最大值为________．
2　[当x≥1时，函数f(x)＝为减函数，所以f(x)在x＝1处取得最大值，为f(1)＝1；当x＜1时，易知函数f(x)＝－x2＋2在x＝0处取得最大值，为f(0)＝2.
故函数f(x)的最大值为2.]
[规律方法]　求函数值域的几个常见类型
(1)若所给函数能够判断单调性，可直接利用单调性求解.
(2)形如求函数的值域或最值，可先将函数解析式变为的形式，再用单调性求解.
(3)分段函数的最值，先求每一个子区间上的最值，则各个区间上最大值中的最大者为分段函数的最大值，各个区间上最小值中的最小者作为分段函数的最小值.
(4)求复合函数y＝f(g(x))的值域，可先求g(x)的值域，再求y＝f(g(x))的值域.,特别地：若函数解析式的几何意义较明显，(如距离、斜率等)或函数图象易作出，可用数形结合法求解.


函数单调性的应用
►考法1　比较函数值的大小
【例2】　已知函数f(x)的图象向左平移1个单位后关于y轴对称，当x2＞x1＞1时，[f(x2)－f(x1)](x2－x1)＜0恒成立，设a＝f，b＝f(2)，c＝f(3)，则a，b，c的大小关系为( )
A．c＞a＞b B．c＞b＞a
C．a＞c＞b D．b＞a＞c
D　[因为f(x)的图象关于直线x＝1对称．由此可得f＝f.由x2＞x1＞1时，[f(x2)－f(x1)](x2－x1)＜0恒成立，知f(x)在(1，＋∞)上单调递减．
因为1＜2＜＜3，所以f(2)＞f＞f(3)，所以b＞a＞c.]
►考法2　解函数不等式
【例3】　(2019·青岛模拟)已知函数f(x)＝x3＋sin x，x∈(－1,1)，则满足f(a2－1)＋f(a－1)＞0的a的取值范围是( )
A．(0,2) B．(1，)
C．(1,2) D．(0，)
B　[由题意知f(－x)＝(－x)3＋sin(－x)＝－x3－sin x＝－(x3＋sin x)＝－f(x)，x∈(－1,1)，
∴f(x)在区间(－1,1)上是奇函数．
又f′(x)＝3x2＋cos x＞0，
∴f(x)在区间(－1,1)上单调递增，
∵f(a2－1)＋f(a－1)＞0，
∴－f(a－1)＜f(a2－1)，
∴f(1－a)＜f(a2－1)，
∴解得1＜a＜，故选B.]
►考法3　求参数的值或取值范围
【例4】　(1)若函数f(x)＝ax2＋2x－3在区间(－∞，4)上是单调递增的，则实数a的取值范围是( )
A. B.
C. D.
(2)已知函数f(x)＝若f(x)在(－∞，＋∞)上单调递增，则实数a的取值范围为________．
(1)D　(2)(2,3]　[(1)当a＝0时，f(x)＝2x－3，在定义域R上是单调递增的，故在(－∞，4)上单调递增；
当a≠0时，二次函数f(x)的对称轴为x＝－，
因为f(x)在(－∞，4)上单调递增，
所以a＜0，且－≥4，解得－≤a＜0.
综上所述，实数a的取值范围是.
(2)要使函数f(x)在R上单调递增，
则有即
解得2＜a≤3，
即实数a的取值范围是(2,3]．]
[规律方法]　函数单调性应用问题的3种常见类型及解题策略
(1)比较大小.
(2)解不等式.利用函数的单调性将“f”符号脱掉，转化为具体的不等式求解，应注意函数的定义域.
(3)利用单调性求参数.
①依据函数的图象或单调性定义，确定函数的单调区间，与已知单调区间比较；
②需注意若函数在区间[a，b]上是单调的，则该函数在此区间的任意子集上也是单调的；
③分段函数的单调性，除注意各段的单调性外，还要注意衔接点的取值.
(1)若f(x)＝－x2＋2ax与g(x)＝在区间[1,2]上都是减函数，则实数a的取值范围是( )
A．(－1,0)∪(0,1) B．(－1,0)∪(0,1]
C．(0,1) D．(0,1]
(2)已知函数f(x)＝若f(2－x2)＞f(x)，则实数x的取值范围是( )
A．(－∞，－1)∪(2，＋∞) B．(－∞，－2)∪(1，＋∞)
C．(－1,2) D．(－2,1)
(3)已知函数y＝f(x)是R上的偶函数，当x1，x2∈(0，＋∞)，x1≠x2时，都有(x1－x2)·[f(x1)－f(x2)]＜0.设a＝ln，b＝(ln π)2，c＝ln，则( )
A．f(a)＞f(b)＞f(c) B．f(b)＞f(a)＞f(c)
C．f(c)＞f(a)＞f(b) D．f(c)＞f(b)＞f(a)
(4)已知函数f(x)＝满足对任意x1≠x2，都有＜0成立，则实数a的取值范围是( )
A. B．(1,2]
C．(1,3) D.
(1)D　(2)D　(3)C　(4)A　[(1)因为f(x)＝－x2＋2ax在[1,2]上是减函数，所以a≤1，又因为g(x)＝在[1,2]上是减函数，所以a＞0，所以0＜a≤1.
(2)因为当x＝0时，两个表达式对应的函数值都为零，
所以函数的图象是一条连续的曲线．
因为当x≤0时，函数f(x)＝x3为增函数，
当x＞0时，f(x)＝ln(x＋1)也是增函数，
所以函数f(x)是定义在R上的增函数．
因此，不等式f(2－x2)＞f(x)等价于2－x2＞x，
即x2＋x－2＜0，解得－2＜x＜1.
(3)由题意可知f(x)在(0，＋∞)上是减函数，且f(a)＝f(|a|)，f(b)＝f(|b|)，f(c)＝f(|c|)，又|a|＝ln π＞1，|b|＝(ln π)2＞|a|，|c|＝ln π，且0＜ln π＜|a|，故|b|＞|a|＞|c|＞0，∴f(|c|)＞f(|a|)＞f(|b|)，即f(c)＞f(a)＞f(b)．
(4)由题意知，函数f(x)在R上是减函数，则解得0＜a≤，故选A.]

(对应学生用书第13页)
1．(2016·全国卷Ⅱ)下列函数中，其定义域和值域分别与函数y＝10lg x的定义域和值域相同的是( )
A．y＝x B．y＝lg x
C．y＝2x D．y＝
D　[函数y＝10lg x的定义域与值域均为(0，＋∞)．
函数y＝x的定义域与值域均为(－∞，＋∞)．
函数y＝lg x的定义域为(0，＋∞)，值域为(－∞，＋∞)．
函数y＝2x的定义域为(－∞，＋∞)，值域为(0，＋∞)．
函数y＝的定义域与值域均为(0，＋∞)．故选D.]
2．(2015·全国卷Ⅱ)设函数f(x)＝ln(1＋|x|)－，则使得f(x)>f(2x－1)成立的x的取值范围是( )
A.
B.∪(1，＋∞)
C.
D.∪
A　[法一：分析f(x)的奇偶性和单调性，然后对所给不等式作出等价转化．
∵f(－x)＝ln(1＋|－x|)－＝f(x)，
∴函数f(x)为偶函数．
∵当x≥0时，f(x)＝ln(1＋x)－，
在(0，＋∞)上y＝ln(1＋x)递增，y＝－也递增，
根据单调性的性质知，f(x)在(0，＋∞)上单调递增．
综上可知：f(x)>f(2x－1)⇔f(|x|)>f(|2x－1|)⇔|x|>|2x－1|⇔x2>(2x－1)2⇔3x2－4x＋1<0⇔ 法二：(特殊值排除法)
令x＝0，此时f(x)＝f(0)＝－1<0，f(2x－1)
＝f(－1)＝ln 2－＝ln 2－ln >0，
∴x＝0不满足f(x)>f(2x－1)，故C错误．
令x＝2，此时f(x)＝f(2)＝ln 3－，f(2x－1)＝f(3)＝ln 4－.∵f(2)－f(3)＝ln 3－ln 4－，
其中ln 3 即f(2)f(2x－1)，
故B，D错误．故选A.]
自我感悟：______________________________________________________
________________________________________________________________
________________________________________________________________