

还剩29页未读,
继续阅读
所属成套资源:2020高考物理一轮复习文档
成套系列资料,整套一键下载
2020年高考物理一轮复习文档:第15章选修3-4第66讲 学案
展开
第66讲 光的折射 全反射
考点一 光的折射
1.光的折射
光从一种介质斜射入另一种介质时,传播方向会改变,这种现象叫做光的折射。如图所示。
2.折射定律
(1)内容:折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比。
(2)表达式:=n。
(3)在光的折射现象中,光路是可逆的。如果让光线逆着原来的折射光线射到界面上,光线就会逆着原来的入射光线发生折射。
3.折射率
(1)定义
光从真空射入某种介质发生折射时,入射角i的正弦与折射角r的正弦之比,用n表示。
(2)定义式:n=。任何介质的折射率总大于1。
(3)意义:介质的折射率反映了介质对光的折射本领。
(4)折射率与光速的关系
某种介质的折射率,等于光在真空中的速度与光在这种介质中的速度之比,即n=。
(5)决定折射率大小的因素:折射率的大小不仅与介质本身有关,还与光的频率有关。同一种介质中,频率越大的色光折射率越大,传播速度越小。
(6)同一种色光,在不同介质中虽然波速、波长不同,但频率相同。
1.关于折射率,下列说法正确的是( )
A.根据=n可知,介质的折射率与入射角的正弦成正比
B.根据=n可知,介质的折射率与折射角的正弦成反比
C.根据n=可知,介质的折射率与介质中的光速成反比
D.同一频率的光由第一种介质进入第二种介质时,折射率与波长成正比
答案 C
解析 介质的折射率n由介质本身及光的频率决定,与入射角、折射角无关,A、B错误;光在不同介质中光速不同,这正是光发生折射的原因,n与v成反比,C正确;把v=λf代入n=得n=,即n与λ成反比,D错误。
2.[教材母题] (人教版选修3-4 P47·例题)如图所示,一个储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶底上的点C,C、B两点相距。求油的折射率和光在油中传播的速度。
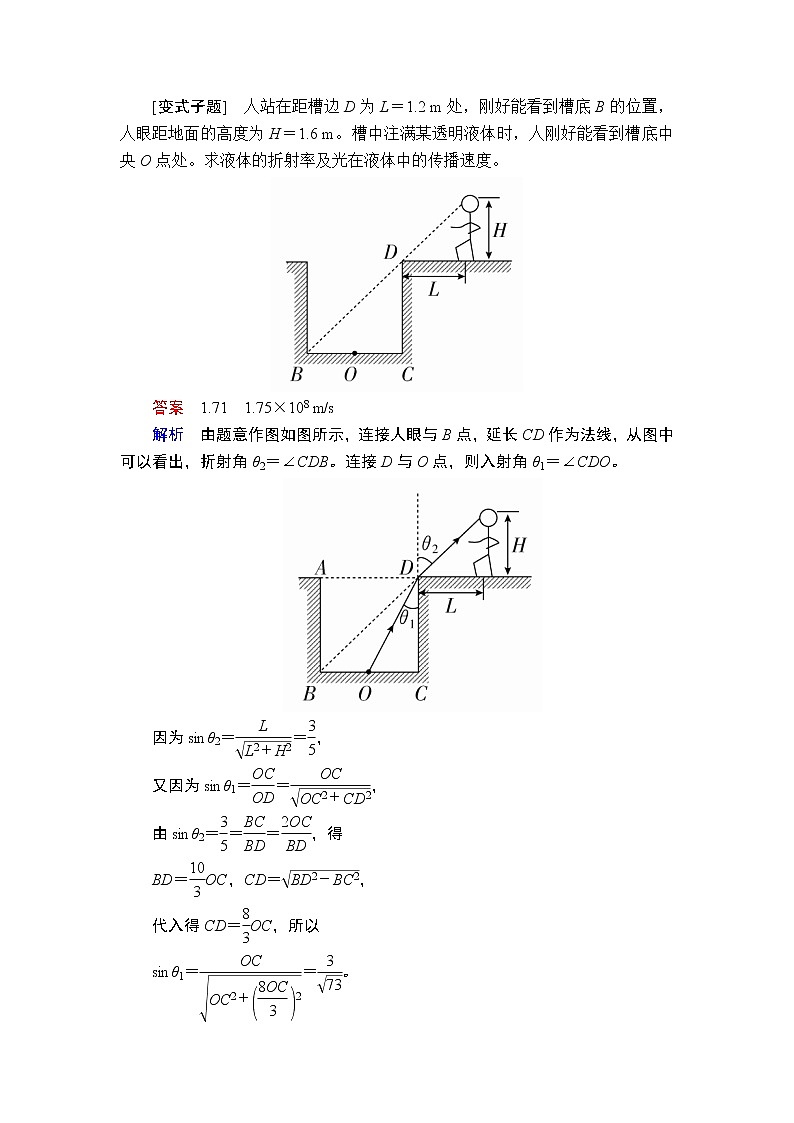
[变式子题] 人站在距槽边D为L=1.2 m处,刚好能看到槽底B的位置,人眼距地面的高度为H=1.6 m。槽中注满某透明液体时,人刚好能看到槽底中央O点处。求液体的折射率及光在液体中的传播速度。
答案 1.71 1.75×108 m/s
解析 由题意作图如图所示,连接人眼与B点,延长CD作为法线,从图中可以看出,折射角θ2=∠CDB。连接D与O点,则入射角θ1=∠CDO。
因为sinθ2==,
又因为sinθ1==,
由sinθ2===,得
BD=OC,CD=,
代入得CD=OC,所以
sinθ1==。
故液体的折射率n==≈1.71,
光在液体中的速度为v=≈1.75×108 m/s。
考点二 测定玻璃的折射率
1.实验原理
如图所示,用插针法确定入射角和折射角,根据n=计算玻璃折射率。
2.实验器材
两侧面平行的玻璃砖、白纸、木板、大头针、图钉、量角器、刻度尺、铅笔。
3.实验步骤与数据处理
(1)把白纸用图钉钉在木板上。
(2)用刻度尺在纸面上作一条直线aa′,过aa′上一点O作垂直于aa′的线段NN′,再过O点作一条线段AO,并使∠NOA即θ1适当大些。
(3)在AO线上竖直地插两枚大头针P1、P2,并使间距适当大些,在白纸上沿直线aa′放上被测玻璃砖。
(4)沿玻璃砖的另一个侧面再作一条直线bb′。
(5)在玻璃砖的bb′一侧白纸上竖直地插一枚大头针P3,使P3恰好能同时挡住aa′一侧所插的大头针P2、P1的像。接着,在玻璃砖的bb′一侧再竖直地插一枚大头针P4,使P4能挡住P3本身以及P1、P2的像。
(6)标记下P1、P2、P3、P4的位置,移去玻璃砖,拔去大头针,过P3、P4作一条直线O′B,交bb′于O′点,连接OO′就是入射光线AO在玻璃砖内的折射光线,折射角为θ2。
(7)用量角器量出入射角θ1和折射角θ2的大小,记入表格内。
(8)用上述方法分别测出入射角是15°、30°、45°、60°和75°时的折射角,查出入射角和折射角的正弦值,记入表格里。
(9)数据处理
①计算法:n=,并取平均值。
②图象法:作出sinθ1sinθ2图象,如图甲所示,n=k。
③辅助线段法:如图乙所示,作辅助线AB垂直于OB,量出A、O,作辅助线CD垂直于OD,量出C、O,则sinθ1=,sinθ2=,即可求出:n==。
④“单位圆”法:以入射点O为圆心,以适当长度R为半径画圆,交入射光线OA于E点,交折射光线OO′于E′点,过E作NN′的垂线EH,过E′作NN′的垂线E′H′。如图丙所示,sinθ1=,sinθ2=,OE=OE′=R,则n==。
4.注意事项与误差分析
(1)实验时,将大头针尽可能竖直地插在纸板上,并且使P1和P2之间、P3与P4之间距离适当大一些,这样可以减小确定光路方向时出现的误差。
(2)入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大,太大会导致反射光太强、折射光太弱,不易确定P3、P4的位置。
(3)在操作时,手不能触摸玻璃砖的光洁光学面,更不能把玻璃砖当尺子画界线。
(4)在实验过程中,玻璃砖与白纸的相对位置不能改变。
在“测定玻璃的折射率”的实验中,
(1)小朱同学在实验桌上看到方木板上有一张白纸,白纸上有如图甲所示的实验器材,他认为除了缺刻度尺还少了一种器材,请你写出所缺器材的名称:________。老师将器材配齐后,他进行实验,图乙是他在操作过程中的一个状态,请你指出第四枚大头针应在图乙中的位置________(填“A”“B”或“C”)。
(2)小红利用方格坐标纸测定玻璃的折射率,如图丙所示,AO是画在纸上的直线,她在直线AO适当位置竖直插上P1、P2两枚大头针,放上半圆形玻璃砖,使其圆心与O重合,然后插上P3、P4两枚大头针,以确定折射光线。其中她确定P3大头针位置的方法应当是________。操作完成后,她用圆规作了一个以O为圆心、半径与玻璃砖半径相同的半圆(如图丙中虚线所示),则她测出玻璃的折射率n=________。
解析 (1)实验器材还缺少大头针;依据光的折射定律,及玻璃砖上下表面平行,那么出射光线与入射光线相互平行,因此第四枚大头针应在图乙中的位置B处。
(2)透过玻璃砖看,P3大头针挡住P1、P2两枚大头针的像;如图,作出法线,过圆与入射光线、折射光线的交点作法线的垂线CA′和DB,由数学知识得,入射角和折射角的正弦值分别为:sini=,sinr=,其中CO=DO,则折射率n====1.5。
答案 (1)大头针 B (2)挡住P1、P2的像 1.5
方法感悟
(1)平行玻璃砖的出射光线和入射光线平行。
(2)对半圆形玻璃砖,入射光线若沿半径,则折射角和入射角均为0°,即光线进入玻璃砖时方向不发生变化。
(3)过出射点作出法线,运用数学知识求出入射角和折射角的正弦值,再由折射定律求出折射率。
(2018·浙江模拟)在用插针法做“测定玻璃砖折射率”的实验中,某同学先在白纸上画出一直线并让待测玻璃砖一界面ab与线重合放置,再进行插针观察,如图所示。梯形abcd是其主截面的边界线,而A、B、C、D为该同学在某次实验时插入的4枚大头针的位置情况。
(1)请在图中完成测量玻璃砖折射率的有关光路图,并标出入射角α和折射角β;
(2)用α和β写出计算折射率的公式n=________;
(3)若所画的cd线比实际界面向外平移了一些,则测得的折射率将________(填“偏小”不变”或“偏大”)。
答案 (1)图见解析 (2) (3)偏大
解析 (1)连接AB作为入射光线,入射点为E,连接CD作为出射光线,出射点为F,连接EF,即为玻璃砖内的折射光线。光路图如图所示:
(2)根据折射定律得:n=。
(3)根据光路图可知,若所画的cd线比实际界面向外平移了一些,折射角β偏小,入射角α不变,根据n=,可知测得的折射率将偏大。
考点三 光的全反射
1.发生全反射的条件
(1)光必须从光密介质射入光疏介质,例如从水中或玻璃中射入空气中。
(2)入射角必须大于或等于临界角。
2.临界角:折射角等于90°时的入射角。若光从光密介质(折射率为n)射向真空或空气时,发生全反射的临界角为C,则sinC=。
3.全反射现象可以从能量的角度去理解:当光由光密介质射向光疏介质时,在入射角逐渐增大的过程中,反射光的能量逐渐增强,折射光的能量逐渐减弱,当入射角等于临界角时,折射光的能量已经减弱为零,这时就发生了全反射。光导纤维就是利用了这一原理。
4.解决全反射问题的一般步骤
(1)确定光是从光密介质进入光疏介质。
(2)应用sinC=确定临界角。
(3)根据题设条件,判定光在传播时是否发生全反射。
(4)如发生全反射,画出入射角等于临界角时的临界光路图。
(5)运用几何关系或三角函数关系以及反射定律等进行分析、判断、运算,解决问题。
1.在自行车的后挡泥板上,常常安装着一个“尾灯”,其实它不是灯,它是用一种透明的塑料制成的,其截面如图所示。夜间,从自行车后方来的汽车灯光照在“尾灯”上时,“尾灯”就变得十分明亮,以便引起汽车司机的注意。从原理上讲,它的功能是利用了( )
A.光的折射 B.光的全反射
C.光的干涉 D.光的衍射
答案 B
解析 全反射可以让反射光的强度更大一些,故B正确。
2.[教材母题] (人教版选修3-4 P53·T6)如图是一个用折射率n=2.4的透明介质做成的四棱柱的横截面图,其中∠A=∠C=90°,∠B=60°。现有一条光线从图示的位置垂直入射到棱镜的AB面上,画出光路图,确定射出的光线。注意:每个面的反射光线和折射光线都不能忽略。
[变式子题] (2018·吉林长春质检)如图所示是一种折射率n=1.5的棱镜,用于某种光学仪器中。现有一束光线沿MN的方向射到棱镜的AB界面上,入射角的大小为i(sini=0.75)。求:
(1)光在棱镜中传播的速率;
(2)此束光线射出棱镜后的方向,写出推导过程并画出光路图(不考虑返回到AB面上的光线)。
答案 (1)2.0×108 m/s (2)见解析
解析 (1)由折射率与光速的关系知
v==2.0×108 m/s。
(2)光路图如图所示,设光线进入棱镜后的折射角为r,
由n=得sinr==0.5
解得r=30°。
光线射到BC界面的入射角
i1=90°-(180°-60°-75°)=45°。
由sinC==C,光线在BC面上发生全反射,光线沿DE方向射到AC边时,与AC边垂直,故此束光线射出棱镜后方向与AC界面垂直。
考点四 光的色散与光路控制
1.光的色散
(1)含有多种颜色的光被分解为单色光的现象称为光的色散。本讲只讨论光的折射中的色散,光的干涉、衍射中也有色散现象,详情见下讲内容。
(2)光折射时的色散
①现象:一束白光通过三棱镜后在屏上会形成彩色光带。
②成因:棱镜材料对不同色光的折射率不同,对红光的折射率最小,红光通过棱镜后的偏折程度最小,对紫光的折射率最大,紫光通过棱镜后的偏折程度最大,从而产生色散现象。
(3)各种色光的比较
2.平行玻璃砖、三棱镜和圆柱体(球)对光路的控制
(2015·重庆高考)虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明。两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图所示。M、N、P、Q点的颜色分别为 ( )
A.紫、红、红、紫 B.红、紫、红、紫
C.红、紫、紫、红 D.紫、红、紫、红
解析 由题图可知,射到M点的光线进入玻璃球时的折射角小于射到N点的光线进入玻璃球时的折射角,所以玻璃对射到M点的光的折射率大于玻璃对射到N点的光的折射率,故M点的颜色为紫色,N点的颜色为红色;同理可得P点的颜色为红色,Q点的颜色为紫色,所以只有A项正确。
答案 A
方法感悟
根据白光中七种色光的频率大小关系、在介质中的折射率大小关系,并结合折射定律及全反射等知识进行分析,常常是解决光的色散问题的关键。
1.(多选)如图所示,从点光源S发出的一细束白光以一定的角度入射到三棱镜的表面,经过三棱镜的折射后发生色散现象,在光屏的ab间形成一条彩色光带。下面的说法中正确的是( )
A.a侧是红光,b侧是紫光
B.在真空中a侧光的波长小于b侧光的波长
C.三棱镜对a侧光的折射率大于对b侧光的折射率
D.在三棱镜中a侧光的速率比b侧光小
E.在三棱镜中a、b两侧光的速率相同
答案 BCD
解析 由题图可以看出,a侧光偏折得较厉害,三棱镜对a侧光的折射率较大,所以a侧光是紫光,波长较短,b侧光是红光,波长较长,因此A错误,B、C正确;又v=,所以三棱镜中a侧光的传播速率小于b侧光的传播速率,D正确,E错误。
2.(多选)频率不同的两束单色光1和2以相同的入射角从同一点射入一厚平行玻璃砖,单色光1、2在玻璃砖中折射角分别为30°和60°,其光路如图所示,下列说法正确的是( )
A.出射光线1和2一定是平行光
B.单色光1的波长大于单色光2的波长
C.在玻璃中单色光1的传播速度大于单色光2的传播速度
D.图中单色光1、2通过玻璃砖所需的时间相等
E.单色光1从玻璃射到空气的全反射临界角小于单色光2从玻璃射到空气的全反射临界角
答案 ADE
解析 光线在平行玻璃砖上表面的折射角等于在下表面
的入射角,由光路可逆性原理可知,出射光线的折射角等于入射光线的入射角,因此出射光线1和2相互平行,A正确;在上表面,单色光1比单色光2偏折程度大,则单色光1的折射率大、频率大、波长短,B错误;根据v=知,单色光1在玻璃砖中的传播速度小,C错误;设入射角为i,玻璃砖的厚度为d,单色光1、单色光2折射角分别为r1=30°,r2=60°,由n=,光在玻璃中传播距离l=,光在玻璃中的传播速度v=,可知光在玻璃中传播时间t===,又sin2r1=sin60°=,sin2r2=sin120°=,所以单色光1与单色光2通过玻璃砖所需时间相等,D正确;根据sinC=知,单色光1的折射率大,则临界角小,E正确。
课后作业
[巩固强化练]
1.(多选)如图所示,MN是介质1和介质2的分界面,介质1、2的绝对折射率分别为n1、n2,一束细光束从介质1射向介质2中,测得θ1=60°,θ2=30°,根据你所学的光学知识判断下列说法正确的是( )
A.介质2相对介质1的相对折射率为
B.光在介质2中的传播速度小于光在介质1中的传播速度
C.介质1相对介质2来说是光密介质
D.光从介质1进入介质2可能发生全反射现象
E.光从介质1进入介质2,光的波长变短
答案 ABE
解析 光从介质1射入介质2时,入射角与折射角的正弦之比叫做介质2相对介质1的相对折射率,所以有n21==,A正确;因介质2相对介质1的相对折射率为,可以得出介质2的绝对折射率大,因n=,所以光在介质2中的传播速度小于光在介质1中的传播速度,B正确;介质2相对介质1来说是光密介质,C错误;光从光密介质射入光疏介质时,有可能发生全反射现象,D错误;光从介质1进入介质2,光的频率不变,速度变小,由v=λf可知,光的波长变短,E正确。
2.一束只含红光和紫光的复色光P垂直于三棱镜的一个侧面射入,后分为两束沿OM和ON方向射出,如图所示。由图可知( )
A.OM为红光,ON为紫光
B.OM为紫光,ON为红光
C.OM为红光,ON为红、紫色复色光
D.OM为紫光,ON为红、紫色复色光
答案 C
解析 因紫光的折射率大于红光的折射率,紫光全反射的临界角小于红光的临界角,入射角相同,发生全反射的一定是紫光,所以OM为红光,红光折射的同时有一部分要发生反射,所以ON应为含有红光和紫光的复色光,C正确。
3.(多选)一束光从某介质进入真空,方向如图所示,则下列判断中正确的是( )
A.该介质的折射率是
B.该介质的折射率是
C.该介质相对真空发生全反射的临界角小于45°
D.光线按如图所示的方向入射,无论怎样改变入射方向都不可能发生全反射现象
E.如果光从真空射向介质,则不可能发生全反射现象
答案 BCE
解析 上面是介质,下面是真空,入射角i=30°,折射角r=60°,则折射率n===,A错误,B正确;sinC==<,则C<45°,C正确;光线按如图所示的方向入射,当入射角大于临界角时,就会发生全反射现象,D错误;光从真空射向介质,不可能发生全反射现象,E正确。
4.(多选)a、b两种单色光组成的光束从玻璃进入空气时,其折射光束如图所示,则关于a、b两束光的说法正确的是( )
A.玻璃对a光的折射率小于对b光的折射率
B.增大入射角时,a光首先发生全反射
C.a光的频率大于b光的频率
D.在真空中a光的波长大于b光的波长
E.分别用这两束光照射双缝干涉实验装置,在光屏上都能出现干涉条纹,a光的相邻条纹间距大于b光
答案 ADE
解析 a光的偏折程度小于b光,所以玻璃对a光的折射率小于对b光的折射率,增大入射角,b光首先发生全反射,A正确,B错误;折射率大的光频率大,所以a光的频率小于b光的频率,C错误;根据c=λf知,a光的波长长,再由Δx=λ,a光的相邻条纹间距大于b光,D、E正确。
5.(多选)如图,一束光沿半径方向射向一块半圆形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线。则( )
A.在玻璃中,a光的传播速度小于b光的传播速度
B.在真空中,a光的波长小于b光的波长
C.玻璃砖对a光的折射率小于对b光的折射率
D.若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失
E.分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距
答案 ABD
解析 从光路图看,入射角相同,a光的折射角较大,所以玻璃砖对a光的折射率较大,a光的频率较大、波长较短,B正确,C错误;根据n=知va
答案
解析 如图所示,设入射角为θ1,折射角为θ2,则sinθ1==,即θ1=30°。
过B点作OD的垂线交于E点,∠BOE=θ1=30°,
又cos∠BOE==,
可得OE=·OB=R,所以ED=OD-OE=R,
则tan∠BDE==,可得∠BDE=30°,
由几何关系可得θ2=60°,折射率n==。
7.如图所示,一束平行于直径AB的单色光照射到玻璃球上,从N点进入玻璃球直接打在B点,在B点反射后从P点射出玻璃球(P点未画出)。已知玻璃球的半径为R,折射率n=,光在真空中的传播速度为c,求:
(1)入射点N与出射点P间的距离;
(2)此单色光由N点经B点传播到P点的时间。
答案 (1)R (2)
解析 (1)在B点的反射光线与入射光线NB关于AB对称,则可知从P点射出的光线与原平行于AB的入射光线平行对称,作出光路图如图所示。
由光路图知θ1=2θ2,
由折射定律得n=,
解得cosθ2=,即θ2=30°,θ1=60°,
则d=Rsinθ1,所以入射点N与出射点P间的距离为2d=R。
(2)该束光线在玻璃球中的路程
s=2·N=2·2Rcosθ2=2R,
光在玻璃球中的速度v==,
光在玻璃球中的时间t==。
[真题模拟练]
8.(2018·全国卷Ⅰ)如图,△ABC为一玻璃三棱镜的横截面,∠A=30°。一束红光垂直AB边射入,从AC边上的D点射出,其折射角为60°,则玻璃对红光的折射率为________。若改用蓝光沿同一路径入射,则光线在D点射出时的折射角________(填“小于”“等于”或“大于”)60°。
答案 大于
解析 根据题述和图示可知,折射角i=60°,入射角r=30°,由折射定律,玻璃对红光的折射率n==。若改用蓝光沿同一路径入射,由于玻璃对蓝光的折射率大于玻璃对红光的折射率,则光线在D点射出时的折射角大于60°。
9.(2018·福建省毕业质量检查模拟(一))如图所示,一束平行的绿光从半圆形玻璃砖的平面垂直入射,OC为中心线,已知在半圆弧上的入射点A的入射光线经折射后与OC的交点为点B,∠AOB=30°,∠ABC=15°,则绿光在该玻璃中的折射率为________,圆形玻璃砖中有光从半圆面透射区域的圆心角为________;若将入射光改为红光,则光从半圆面透射区域的圆心角将________(选填“变小”“不变”或“变大”)。
答案 90° 变大
解析 在A点,由几何知识可得
入射角i=∠AOB=30°
折射角r=∠AOB+∠ABC=45°
则绿光在该玻璃中的折射率为n==。
设光线恰好射到半圆面上D点时发生全反射,其入射角等于临界角C,由sinC=得C=45°
在D点以下有光从半圆面透射而出,则由对称性可知,圆形玻璃砖中有光从半圆面透射区域的圆心角为90°。
红光的折射率小于绿光,临界角大于绿光,则若将入射光改为红光,则发生全反射的临界点向边缘移动,即光从半圆面透射区域的圆心角将变大。
10.(2018·全国卷Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(1)求出射光相对于D点的入射光的偏角;
(2)为实现上述光路,棱镜折射率的取值应在什么范围?
答案 (1)60° (2)≤n<2
解析 (1)如图,光线在BC面上折射,由折射定律有sini1=nsinr1①
式中,n为棱镜的折射率,i1和r1分别是该光线在BC面上的入射角和折射角。
光线在AC面上发生全反射,由反射定律有i2=r2②
式中i2和r2分别是该光线在AC面上的入射角和反射角。
光线在AB面上发生折射,由折射定律有nsini3=sinr3③
式中i3和r3分别是该光线在AB面上的入射角和折射角。由几何关系及②式得i2=r2=60°,r1=i3=30°④
F点的出射光相对于D点的入射光的偏角为
δ=(r1-i1)+(180°-i2-r2)+(r3-i3)⑤
由①③④⑤式得δ=60°⑥
(2)光线在AC面上发生全反射,在AB面上不发生全反射,有
nsini2≥nsinC>nsini3⑦
式中C是全反射临界角,满足nsinC=1⑧
由④⑦⑧式知,棱镜的折射率n的取值范围应为≤n<2。
11.(2018·全国卷Ⅲ)如图,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点作AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点作AB边的垂线交直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
答案
解析 过D点作AB边的垂线NN′,连接OD,则∠ODN=α为来自O点的光线在D点的入射角;设该光线在D点的折射角为β,如图所示。
根据折射定律有nsinα=sinβ①
式中n为三棱镜的折射率
由几何关系可知β=60°②
∠EOF=30°③
在△OEF中有EF=OEsin∠EOF④
由③④式和题给条件得OE=2 cm⑤
根据题给条件可知,△OED为等腰三角形,有α=30°⑥
由①②⑥式得n=。
12.(2017·全国卷Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
答案 1.55
解析 设从光源发出直接射到D点的光线的入射角为i1,折射角为r1。在剖面内作光源相对于反光壁的镜像对称点C,连接C、D,交反光壁于E点,由光源射向E点的光线,反射后沿ED射向D点。设光线在D点的入射角为i2,折射角为r2,如图所示。
设液体的折射率为n,由折射定律有
nsini1=sinr1①
nsini2=sinr2②
由题意知r1+r2=90°③
联立①②③式得n2=④
由几何关系可知sini1==⑤
sini2==⑥
联立④⑤⑥式得n≈1.55。
13.(2017·全国卷Ⅰ)如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R。已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)。求该玻璃的折射率。
答案 1.43
解析 如图,根据光路的对称性和光路可逆性,从半球面射入的折射光线,将从圆柱体底面中心C点反射。
设光线在半球面的入射角为i,折射角为r。
由折射定律有sini=nsinr①
由正弦定理有=②
由几何关系,入射点的法线与OC的夹角为i。
由题设条件和几何关系有sini=③
式中L是入射光线与OC的距离。由②③式和题给数据得sinr=④
由①③④式和题给数据得n=≈1.43。
14.(2017·全国卷Ⅲ)如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线)。已知玻璃的折射率为1.5。现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线)。求:
(1)从球面射出的光线对应的入射光线到光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离。
答案 (1)R (2)2.74R
解析 (1)设光线在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l。
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有
nsinic=1②
由几何关系有sinic=③
联立①②③式并利用题给条件,得l=R④
(2)设与光轴相距的光线从A点入射,在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有nsini1=sinr1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有=⑥
由几何关系有
∠C=r1-i1⑦
sini1=⑧
联立⑤⑥⑦⑧式及题给条件得
OC=R≈2.74R。
15.(2016·全国卷Ⅰ)如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0 m。从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为。
(1)求池内的水深;
(2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m。当他看到正前下方的点光源A时,他的眼睛所接受的光线与竖直方向的夹角恰好为45°,求救生员的眼睛到池边的水平距离(结果保留1位有效数字)。
答案 (1)2.6 m (2)0.7 m
解析 (1)如图,设到达池边的光线的入射角为i。依题意,水的折射率n=,光线的折射角θ=90°。由折射定律有
nsini=sinθ①
由几何关系有
sini=②
式中,l=3 m,h是池内水的深度。
联立①②式并代入题给数据得h= m≈2.6 m。③
(2)设此时救生员的眼睛到池边的水平距离为x。依题意,救生员的视线与竖直方向的夹角为θ′=45°。由折射定律有
nsini′=sinθ′④
式中,i′是光线在水面的入射角。设池底点光源A到水面入射点的水平距离为a。由几何关系有
sini′=⑤
x+l=a+h′⑥
式中h′=2 m。
联立③④⑤⑥式得x= m≈0.7 m。
16.(2016·全国卷Ⅲ)如图,玻璃球冠的折射率为,其底面镀银,底面的半径是球半径的倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点。求该光线从球面射出的方向相对于其初始入射方向的偏角。
答案 150°
解析 设球半径为R,球冠底面中心为O′,连接OO′,则OO′⊥AB。
令∠OAO′=α,有
cosα===①
即α=30°②
由题意MA⊥AB③
所以∠OAM=60°
设图中N点为光线在球冠内底面上的反射点,所考虑的光线的光路图如图所示。设光线在M点的入射角为i,折射角为r,在N点的入射角为i′,反射角为i″,玻璃折射率为n。由于△OAM为等边三角形,有
i=60°④
由折射定律有sini=nsinr⑤
代入题给条件n=得r=30°⑥
作底面在N点的法线NE,由于NE∥AM,有
i′=30°⑦
根据反射定律,有i″=30°⑧
连接ON,由几何关系知△MAN≌△MON,故有∠MNO=60°⑨
由⑦⑨式得∠ENO=30°⑩
于是∠ENO为反射角,NO为反射光线。这一反射光线经球面再次折射后不改变方向。所以,射出玻璃球冠的光线相对于入射光线的偏角β为β=180°-∠ENO=150°。
17.(2018·抚顺模拟)如图所示,空气中有一折射率为的玻璃柱体,其横截面是圆心角为90°、半径为R的扇形OAB。一束平行光平行于横截面,以45°入射角照射到OA上,OB不透光。若只考虑首次入射到圆弧AB上的光,则AB上有光透出部分的弧长为多长?
答案 πR
解析 由sinC=,可知光在玻璃柱中发生全反射的临界角C=45°,=,
所有光线从AO进入玻璃柱后的折射角均为r=30°,
从O点入射后的折射光线将沿半径从C点射出,假设从E点入射的光线经折射后到达D点时刚好发生全反射,
则∠ODE=45°。
如图所示,由几何关系可知θ=45°,
故AB上有光透出部分的弧长为πR。
第66讲 光的折射 全反射
考点一 光的折射
1.光的折射
光从一种介质斜射入另一种介质时,传播方向会改变,这种现象叫做光的折射。如图所示。
2.折射定律
(1)内容:折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比。
(2)表达式:=n。
(3)在光的折射现象中,光路是可逆的。如果让光线逆着原来的折射光线射到界面上,光线就会逆着原来的入射光线发生折射。
3.折射率
(1)定义
光从真空射入某种介质发生折射时,入射角i的正弦与折射角r的正弦之比,用n表示。
(2)定义式:n=。任何介质的折射率总大于1。
(3)意义:介质的折射率反映了介质对光的折射本领。
(4)折射率与光速的关系
某种介质的折射率,等于光在真空中的速度与光在这种介质中的速度之比,即n=。
(5)决定折射率大小的因素:折射率的大小不仅与介质本身有关,还与光的频率有关。同一种介质中,频率越大的色光折射率越大,传播速度越小。
(6)同一种色光,在不同介质中虽然波速、波长不同,但频率相同。
1.关于折射率,下列说法正确的是( )
A.根据=n可知,介质的折射率与入射角的正弦成正比
B.根据=n可知,介质的折射率与折射角的正弦成反比
C.根据n=可知,介质的折射率与介质中的光速成反比
D.同一频率的光由第一种介质进入第二种介质时,折射率与波长成正比
答案 C
解析 介质的折射率n由介质本身及光的频率决定,与入射角、折射角无关,A、B错误;光在不同介质中光速不同,这正是光发生折射的原因,n与v成反比,C正确;把v=λf代入n=得n=,即n与λ成反比,D错误。
2.[教材母题] (人教版选修3-4 P47·例题)如图所示,一个储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶底上的点C,C、B两点相距。求油的折射率和光在油中传播的速度。
[变式子题] 人站在距槽边D为L=1.2 m处,刚好能看到槽底B的位置,人眼距地面的高度为H=1.6 m。槽中注满某透明液体时,人刚好能看到槽底中央O点处。求液体的折射率及光在液体中的传播速度。
答案 1.71 1.75×108 m/s
解析 由题意作图如图所示,连接人眼与B点,延长CD作为法线,从图中可以看出,折射角θ2=∠CDB。连接D与O点,则入射角θ1=∠CDO。
因为sinθ2==,
又因为sinθ1==,
由sinθ2===,得
BD=OC,CD=,
代入得CD=OC,所以
sinθ1==。
故液体的折射率n==≈1.71,
光在液体中的速度为v=≈1.75×108 m/s。
考点二 测定玻璃的折射率
1.实验原理
如图所示,用插针法确定入射角和折射角,根据n=计算玻璃折射率。
2.实验器材
两侧面平行的玻璃砖、白纸、木板、大头针、图钉、量角器、刻度尺、铅笔。
3.实验步骤与数据处理
(1)把白纸用图钉钉在木板上。
(2)用刻度尺在纸面上作一条直线aa′,过aa′上一点O作垂直于aa′的线段NN′,再过O点作一条线段AO,并使∠NOA即θ1适当大些。
(3)在AO线上竖直地插两枚大头针P1、P2,并使间距适当大些,在白纸上沿直线aa′放上被测玻璃砖。
(4)沿玻璃砖的另一个侧面再作一条直线bb′。
(5)在玻璃砖的bb′一侧白纸上竖直地插一枚大头针P3,使P3恰好能同时挡住aa′一侧所插的大头针P2、P1的像。接着,在玻璃砖的bb′一侧再竖直地插一枚大头针P4,使P4能挡住P3本身以及P1、P2的像。
(6)标记下P1、P2、P3、P4的位置,移去玻璃砖,拔去大头针,过P3、P4作一条直线O′B,交bb′于O′点,连接OO′就是入射光线AO在玻璃砖内的折射光线,折射角为θ2。
(7)用量角器量出入射角θ1和折射角θ2的大小,记入表格内。
(8)用上述方法分别测出入射角是15°、30°、45°、60°和75°时的折射角,查出入射角和折射角的正弦值,记入表格里。
(9)数据处理
①计算法:n=,并取平均值。
②图象法:作出sinθ1sinθ2图象,如图甲所示,n=k。
③辅助线段法:如图乙所示,作辅助线AB垂直于OB,量出A、O,作辅助线CD垂直于OD,量出C、O,则sinθ1=,sinθ2=,即可求出:n==。
④“单位圆”法:以入射点O为圆心,以适当长度R为半径画圆,交入射光线OA于E点,交折射光线OO′于E′点,过E作NN′的垂线EH,过E′作NN′的垂线E′H′。如图丙所示,sinθ1=,sinθ2=,OE=OE′=R,则n==。
4.注意事项与误差分析
(1)实验时,将大头针尽可能竖直地插在纸板上,并且使P1和P2之间、P3与P4之间距离适当大一些,这样可以减小确定光路方向时出现的误差。
(2)入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大,太大会导致反射光太强、折射光太弱,不易确定P3、P4的位置。
(3)在操作时,手不能触摸玻璃砖的光洁光学面,更不能把玻璃砖当尺子画界线。
(4)在实验过程中,玻璃砖与白纸的相对位置不能改变。
在“测定玻璃的折射率”的实验中,
(1)小朱同学在实验桌上看到方木板上有一张白纸,白纸上有如图甲所示的实验器材,他认为除了缺刻度尺还少了一种器材,请你写出所缺器材的名称:________。老师将器材配齐后,他进行实验,图乙是他在操作过程中的一个状态,请你指出第四枚大头针应在图乙中的位置________(填“A”“B”或“C”)。
(2)小红利用方格坐标纸测定玻璃的折射率,如图丙所示,AO是画在纸上的直线,她在直线AO适当位置竖直插上P1、P2两枚大头针,放上半圆形玻璃砖,使其圆心与O重合,然后插上P3、P4两枚大头针,以确定折射光线。其中她确定P3大头针位置的方法应当是________。操作完成后,她用圆规作了一个以O为圆心、半径与玻璃砖半径相同的半圆(如图丙中虚线所示),则她测出玻璃的折射率n=________。
解析 (1)实验器材还缺少大头针;依据光的折射定律,及玻璃砖上下表面平行,那么出射光线与入射光线相互平行,因此第四枚大头针应在图乙中的位置B处。
(2)透过玻璃砖看,P3大头针挡住P1、P2两枚大头针的像;如图,作出法线,过圆与入射光线、折射光线的交点作法线的垂线CA′和DB,由数学知识得,入射角和折射角的正弦值分别为:sini=,sinr=,其中CO=DO,则折射率n====1.5。
答案 (1)大头针 B (2)挡住P1、P2的像 1.5
方法感悟
(1)平行玻璃砖的出射光线和入射光线平行。
(2)对半圆形玻璃砖,入射光线若沿半径,则折射角和入射角均为0°,即光线进入玻璃砖时方向不发生变化。
(3)过出射点作出法线,运用数学知识求出入射角和折射角的正弦值,再由折射定律求出折射率。
(2018·浙江模拟)在用插针法做“测定玻璃砖折射率”的实验中,某同学先在白纸上画出一直线并让待测玻璃砖一界面ab与线重合放置,再进行插针观察,如图所示。梯形abcd是其主截面的边界线,而A、B、C、D为该同学在某次实验时插入的4枚大头针的位置情况。
(1)请在图中完成测量玻璃砖折射率的有关光路图,并标出入射角α和折射角β;
(2)用α和β写出计算折射率的公式n=________;
(3)若所画的cd线比实际界面向外平移了一些,则测得的折射率将________(填“偏小”不变”或“偏大”)。
答案 (1)图见解析 (2) (3)偏大
解析 (1)连接AB作为入射光线,入射点为E,连接CD作为出射光线,出射点为F,连接EF,即为玻璃砖内的折射光线。光路图如图所示:
(2)根据折射定律得:n=。
(3)根据光路图可知,若所画的cd线比实际界面向外平移了一些,折射角β偏小,入射角α不变,根据n=,可知测得的折射率将偏大。
考点三 光的全反射
1.发生全反射的条件
(1)光必须从光密介质射入光疏介质,例如从水中或玻璃中射入空气中。
(2)入射角必须大于或等于临界角。
2.临界角:折射角等于90°时的入射角。若光从光密介质(折射率为n)射向真空或空气时,发生全反射的临界角为C,则sinC=。
3.全反射现象可以从能量的角度去理解:当光由光密介质射向光疏介质时,在入射角逐渐增大的过程中,反射光的能量逐渐增强,折射光的能量逐渐减弱,当入射角等于临界角时,折射光的能量已经减弱为零,这时就发生了全反射。光导纤维就是利用了这一原理。
4.解决全反射问题的一般步骤
(1)确定光是从光密介质进入光疏介质。
(2)应用sinC=确定临界角。
(3)根据题设条件,判定光在传播时是否发生全反射。
(4)如发生全反射,画出入射角等于临界角时的临界光路图。
(5)运用几何关系或三角函数关系以及反射定律等进行分析、判断、运算,解决问题。
1.在自行车的后挡泥板上,常常安装着一个“尾灯”,其实它不是灯,它是用一种透明的塑料制成的,其截面如图所示。夜间,从自行车后方来的汽车灯光照在“尾灯”上时,“尾灯”就变得十分明亮,以便引起汽车司机的注意。从原理上讲,它的功能是利用了( )
A.光的折射 B.光的全反射
C.光的干涉 D.光的衍射
答案 B
解析 全反射可以让反射光的强度更大一些,故B正确。
2.[教材母题] (人教版选修3-4 P53·T6)如图是一个用折射率n=2.4的透明介质做成的四棱柱的横截面图,其中∠A=∠C=90°,∠B=60°。现有一条光线从图示的位置垂直入射到棱镜的AB面上,画出光路图,确定射出的光线。注意:每个面的反射光线和折射光线都不能忽略。
[变式子题] (2018·吉林长春质检)如图所示是一种折射率n=1.5的棱镜,用于某种光学仪器中。现有一束光线沿MN的方向射到棱镜的AB界面上,入射角的大小为i(sini=0.75)。求:
(1)光在棱镜中传播的速率;
(2)此束光线射出棱镜后的方向,写出推导过程并画出光路图(不考虑返回到AB面上的光线)。
答案 (1)2.0×108 m/s (2)见解析
解析 (1)由折射率与光速的关系知
v==2.0×108 m/s。
(2)光路图如图所示,设光线进入棱镜后的折射角为r,
由n=得sinr==0.5
解得r=30°。
光线射到BC界面的入射角
i1=90°-(180°-60°-75°)=45°。
由sinC==
考点四 光的色散与光路控制
1.光的色散
(1)含有多种颜色的光被分解为单色光的现象称为光的色散。本讲只讨论光的折射中的色散,光的干涉、衍射中也有色散现象,详情见下讲内容。
(2)光折射时的色散
①现象:一束白光通过三棱镜后在屏上会形成彩色光带。
②成因:棱镜材料对不同色光的折射率不同,对红光的折射率最小,红光通过棱镜后的偏折程度最小,对紫光的折射率最大,紫光通过棱镜后的偏折程度最大,从而产生色散现象。
(3)各种色光的比较
2.平行玻璃砖、三棱镜和圆柱体(球)对光路的控制
(2015·重庆高考)虹和霓是太阳光在水珠内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明。两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图所示。M、N、P、Q点的颜色分别为 ( )
A.紫、红、红、紫 B.红、紫、红、紫
C.红、紫、紫、红 D.紫、红、紫、红
解析 由题图可知,射到M点的光线进入玻璃球时的折射角小于射到N点的光线进入玻璃球时的折射角,所以玻璃对射到M点的光的折射率大于玻璃对射到N点的光的折射率,故M点的颜色为紫色,N点的颜色为红色;同理可得P点的颜色为红色,Q点的颜色为紫色,所以只有A项正确。
答案 A
方法感悟
根据白光中七种色光的频率大小关系、在介质中的折射率大小关系,并结合折射定律及全反射等知识进行分析,常常是解决光的色散问题的关键。
1.(多选)如图所示,从点光源S发出的一细束白光以一定的角度入射到三棱镜的表面,经过三棱镜的折射后发生色散现象,在光屏的ab间形成一条彩色光带。下面的说法中正确的是( )
A.a侧是红光,b侧是紫光
B.在真空中a侧光的波长小于b侧光的波长
C.三棱镜对a侧光的折射率大于对b侧光的折射率
D.在三棱镜中a侧光的速率比b侧光小
E.在三棱镜中a、b两侧光的速率相同
答案 BCD
解析 由题图可以看出,a侧光偏折得较厉害,三棱镜对a侧光的折射率较大,所以a侧光是紫光,波长较短,b侧光是红光,波长较长,因此A错误,B、C正确;又v=,所以三棱镜中a侧光的传播速率小于b侧光的传播速率,D正确,E错误。
2.(多选)频率不同的两束单色光1和2以相同的入射角从同一点射入一厚平行玻璃砖,单色光1、2在玻璃砖中折射角分别为30°和60°,其光路如图所示,下列说法正确的是( )
A.出射光线1和2一定是平行光
B.单色光1的波长大于单色光2的波长
C.在玻璃中单色光1的传播速度大于单色光2的传播速度
D.图中单色光1、2通过玻璃砖所需的时间相等
E.单色光1从玻璃射到空气的全反射临界角小于单色光2从玻璃射到空气的全反射临界角
答案 ADE
解析 光线在平行玻璃砖上表面的折射角等于在下表面
的入射角,由光路可逆性原理可知,出射光线的折射角等于入射光线的入射角,因此出射光线1和2相互平行,A正确;在上表面,单色光1比单色光2偏折程度大,则单色光1的折射率大、频率大、波长短,B错误;根据v=知,单色光1在玻璃砖中的传播速度小,C错误;设入射角为i,玻璃砖的厚度为d,单色光1、单色光2折射角分别为r1=30°,r2=60°,由n=,光在玻璃中传播距离l=,光在玻璃中的传播速度v=,可知光在玻璃中传播时间t===,又sin2r1=sin60°=,sin2r2=sin120°=,所以单色光1与单色光2通过玻璃砖所需时间相等,D正确;根据sinC=知,单色光1的折射率大,则临界角小,E正确。
课后作业
[巩固强化练]
1.(多选)如图所示,MN是介质1和介质2的分界面,介质1、2的绝对折射率分别为n1、n2,一束细光束从介质1射向介质2中,测得θ1=60°,θ2=30°,根据你所学的光学知识判断下列说法正确的是( )
A.介质2相对介质1的相对折射率为
B.光在介质2中的传播速度小于光在介质1中的传播速度
C.介质1相对介质2来说是光密介质
D.光从介质1进入介质2可能发生全反射现象
E.光从介质1进入介质2,光的波长变短
答案 ABE
解析 光从介质1射入介质2时,入射角与折射角的正弦之比叫做介质2相对介质1的相对折射率,所以有n21==,A正确;因介质2相对介质1的相对折射率为,可以得出介质2的绝对折射率大,因n=,所以光在介质2中的传播速度小于光在介质1中的传播速度,B正确;介质2相对介质1来说是光密介质,C错误;光从光密介质射入光疏介质时,有可能发生全反射现象,D错误;光从介质1进入介质2,光的频率不变,速度变小,由v=λf可知,光的波长变短,E正确。
2.一束只含红光和紫光的复色光P垂直于三棱镜的一个侧面射入,后分为两束沿OM和ON方向射出,如图所示。由图可知( )
A.OM为红光,ON为紫光
B.OM为紫光,ON为红光
C.OM为红光,ON为红、紫色复色光
D.OM为紫光,ON为红、紫色复色光
答案 C
解析 因紫光的折射率大于红光的折射率,紫光全反射的临界角小于红光的临界角,入射角相同,发生全反射的一定是紫光,所以OM为红光,红光折射的同时有一部分要发生反射,所以ON应为含有红光和紫光的复色光,C正确。
3.(多选)一束光从某介质进入真空,方向如图所示,则下列判断中正确的是( )
A.该介质的折射率是
B.该介质的折射率是
C.该介质相对真空发生全反射的临界角小于45°
D.光线按如图所示的方向入射,无论怎样改变入射方向都不可能发生全反射现象
E.如果光从真空射向介质,则不可能发生全反射现象
答案 BCE
解析 上面是介质,下面是真空,入射角i=30°,折射角r=60°,则折射率n===,A错误,B正确;sinC==<,则C<45°,C正确;光线按如图所示的方向入射,当入射角大于临界角时,就会发生全反射现象,D错误;光从真空射向介质,不可能发生全反射现象,E正确。
4.(多选)a、b两种单色光组成的光束从玻璃进入空气时,其折射光束如图所示,则关于a、b两束光的说法正确的是( )
A.玻璃对a光的折射率小于对b光的折射率
B.增大入射角时,a光首先发生全反射
C.a光的频率大于b光的频率
D.在真空中a光的波长大于b光的波长
E.分别用这两束光照射双缝干涉实验装置,在光屏上都能出现干涉条纹,a光的相邻条纹间距大于b光
答案 ADE
解析 a光的偏折程度小于b光,所以玻璃对a光的折射率小于对b光的折射率,增大入射角,b光首先发生全反射,A正确,B错误;折射率大的光频率大,所以a光的频率小于b光的频率,C错误;根据c=λf知,a光的波长长,再由Δx=λ,a光的相邻条纹间距大于b光,D、E正确。
5.(多选)如图,一束光沿半径方向射向一块半圆形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线。则( )
A.在玻璃中,a光的传播速度小于b光的传播速度
B.在真空中,a光的波长小于b光的波长
C.玻璃砖对a光的折射率小于对b光的折射率
D.若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失
E.分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距
答案 ABD
解析 从光路图看,入射角相同,a光的折射角较大,所以玻璃砖对a光的折射率较大,a光的频率较大、波长较短,B正确,C错误;根据n=知va
答案
解析 如图所示,设入射角为θ1,折射角为θ2,则sinθ1==,即θ1=30°。
过B点作OD的垂线交于E点,∠BOE=θ1=30°,
又cos∠BOE==,
可得OE=·OB=R,所以ED=OD-OE=R,
则tan∠BDE==,可得∠BDE=30°,
由几何关系可得θ2=60°,折射率n==。
7.如图所示,一束平行于直径AB的单色光照射到玻璃球上,从N点进入玻璃球直接打在B点,在B点反射后从P点射出玻璃球(P点未画出)。已知玻璃球的半径为R,折射率n=,光在真空中的传播速度为c,求:
(1)入射点N与出射点P间的距离;
(2)此单色光由N点经B点传播到P点的时间。
答案 (1)R (2)
解析 (1)在B点的反射光线与入射光线NB关于AB对称,则可知从P点射出的光线与原平行于AB的入射光线平行对称,作出光路图如图所示。
由光路图知θ1=2θ2,
由折射定律得n=,
解得cosθ2=,即θ2=30°,θ1=60°,
则d=Rsinθ1,所以入射点N与出射点P间的距离为2d=R。
(2)该束光线在玻璃球中的路程
s=2·N=2·2Rcosθ2=2R,
光在玻璃球中的速度v==,
光在玻璃球中的时间t==。
[真题模拟练]
8.(2018·全国卷Ⅰ)如图,△ABC为一玻璃三棱镜的横截面,∠A=30°。一束红光垂直AB边射入,从AC边上的D点射出,其折射角为60°,则玻璃对红光的折射率为________。若改用蓝光沿同一路径入射,则光线在D点射出时的折射角________(填“小于”“等于”或“大于”)60°。
答案 大于
解析 根据题述和图示可知,折射角i=60°,入射角r=30°,由折射定律,玻璃对红光的折射率n==。若改用蓝光沿同一路径入射,由于玻璃对蓝光的折射率大于玻璃对红光的折射率,则光线在D点射出时的折射角大于60°。
9.(2018·福建省毕业质量检查模拟(一))如图所示,一束平行的绿光从半圆形玻璃砖的平面垂直入射,OC为中心线,已知在半圆弧上的入射点A的入射光线经折射后与OC的交点为点B,∠AOB=30°,∠ABC=15°,则绿光在该玻璃中的折射率为________,圆形玻璃砖中有光从半圆面透射区域的圆心角为________;若将入射光改为红光,则光从半圆面透射区域的圆心角将________(选填“变小”“不变”或“变大”)。
答案 90° 变大
解析 在A点,由几何知识可得
入射角i=∠AOB=30°
折射角r=∠AOB+∠ABC=45°
则绿光在该玻璃中的折射率为n==。
设光线恰好射到半圆面上D点时发生全反射,其入射角等于临界角C,由sinC=得C=45°
在D点以下有光从半圆面透射而出,则由对称性可知,圆形玻璃砖中有光从半圆面透射区域的圆心角为90°。
红光的折射率小于绿光,临界角大于绿光,则若将入射光改为红光,则发生全反射的临界点向边缘移动,即光从半圆面透射区域的圆心角将变大。
10.(2018·全国卷Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(1)求出射光相对于D点的入射光的偏角;
(2)为实现上述光路,棱镜折射率的取值应在什么范围?
答案 (1)60° (2)≤n<2
解析 (1)如图,光线在BC面上折射,由折射定律有sini1=nsinr1①
式中,n为棱镜的折射率,i1和r1分别是该光线在BC面上的入射角和折射角。
光线在AC面上发生全反射,由反射定律有i2=r2②
式中i2和r2分别是该光线在AC面上的入射角和反射角。
光线在AB面上发生折射,由折射定律有nsini3=sinr3③
式中i3和r3分别是该光线在AB面上的入射角和折射角。由几何关系及②式得i2=r2=60°,r1=i3=30°④
F点的出射光相对于D点的入射光的偏角为
δ=(r1-i1)+(180°-i2-r2)+(r3-i3)⑤
由①③④⑤式得δ=60°⑥
(2)光线在AC面上发生全反射,在AB面上不发生全反射,有
nsini2≥nsinC>nsini3⑦
式中C是全反射临界角,满足nsinC=1⑧
由④⑦⑧式知,棱镜的折射率n的取值范围应为≤n<2。
11.(2018·全国卷Ⅲ)如图,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点作AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点作AB边的垂线交直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
答案
解析 过D点作AB边的垂线NN′,连接OD,则∠ODN=α为来自O点的光线在D点的入射角;设该光线在D点的折射角为β,如图所示。
根据折射定律有nsinα=sinβ①
式中n为三棱镜的折射率
由几何关系可知β=60°②
∠EOF=30°③
在△OEF中有EF=OEsin∠EOF④
由③④式和题给条件得OE=2 cm⑤
根据题给条件可知,△OED为等腰三角形,有α=30°⑥
由①②⑥式得n=。
12.(2017·全国卷Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
答案 1.55
解析 设从光源发出直接射到D点的光线的入射角为i1,折射角为r1。在剖面内作光源相对于反光壁的镜像对称点C,连接C、D,交反光壁于E点,由光源射向E点的光线,反射后沿ED射向D点。设光线在D点的入射角为i2,折射角为r2,如图所示。
设液体的折射率为n,由折射定律有
nsini1=sinr1①
nsini2=sinr2②
由题意知r1+r2=90°③
联立①②③式得n2=④
由几何关系可知sini1==⑤
sini2==⑥
联立④⑤⑥式得n≈1.55。
13.(2017·全国卷Ⅰ)如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R。已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)。求该玻璃的折射率。
答案 1.43
解析 如图,根据光路的对称性和光路可逆性,从半球面射入的折射光线,将从圆柱体底面中心C点反射。
设光线在半球面的入射角为i,折射角为r。
由折射定律有sini=nsinr①
由正弦定理有=②
由几何关系,入射点的法线与OC的夹角为i。
由题设条件和几何关系有sini=③
式中L是入射光线与OC的距离。由②③式和题给数据得sinr=④
由①③④式和题给数据得n=≈1.43。
14.(2017·全国卷Ⅲ)如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线)。已知玻璃的折射率为1.5。现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线)。求:
(1)从球面射出的光线对应的入射光线到光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离。
答案 (1)R (2)2.74R
解析 (1)设光线在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l。
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有
nsinic=1②
由几何关系有sinic=③
联立①②③式并利用题给条件,得l=R④
(2)设与光轴相距的光线从A点入射,在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有nsini1=sinr1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有=⑥
由几何关系有
∠C=r1-i1⑦
sini1=⑧
联立⑤⑥⑦⑧式及题给条件得
OC=R≈2.74R。
15.(2016·全国卷Ⅰ)如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0 m。从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为。
(1)求池内的水深;
(2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m。当他看到正前下方的点光源A时,他的眼睛所接受的光线与竖直方向的夹角恰好为45°,求救生员的眼睛到池边的水平距离(结果保留1位有效数字)。
答案 (1)2.6 m (2)0.7 m
解析 (1)如图,设到达池边的光线的入射角为i。依题意,水的折射率n=,光线的折射角θ=90°。由折射定律有
nsini=sinθ①
由几何关系有
sini=②
式中,l=3 m,h是池内水的深度。
联立①②式并代入题给数据得h= m≈2.6 m。③
(2)设此时救生员的眼睛到池边的水平距离为x。依题意,救生员的视线与竖直方向的夹角为θ′=45°。由折射定律有
nsini′=sinθ′④
式中,i′是光线在水面的入射角。设池底点光源A到水面入射点的水平距离为a。由几何关系有
sini′=⑤
x+l=a+h′⑥
式中h′=2 m。
联立③④⑤⑥式得x= m≈0.7 m。
16.(2016·全国卷Ⅲ)如图,玻璃球冠的折射率为,其底面镀银,底面的半径是球半径的倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点。求该光线从球面射出的方向相对于其初始入射方向的偏角。
答案 150°
解析 设球半径为R,球冠底面中心为O′,连接OO′,则OO′⊥AB。
令∠OAO′=α,有
cosα===①
即α=30°②
由题意MA⊥AB③
所以∠OAM=60°
设图中N点为光线在球冠内底面上的反射点,所考虑的光线的光路图如图所示。设光线在M点的入射角为i,折射角为r,在N点的入射角为i′,反射角为i″,玻璃折射率为n。由于△OAM为等边三角形,有
i=60°④
由折射定律有sini=nsinr⑤
代入题给条件n=得r=30°⑥
作底面在N点的法线NE,由于NE∥AM,有
i′=30°⑦
根据反射定律,有i″=30°⑧
连接ON,由几何关系知△MAN≌△MON,故有∠MNO=60°⑨
由⑦⑨式得∠ENO=30°⑩
于是∠ENO为反射角,NO为反射光线。这一反射光线经球面再次折射后不改变方向。所以,射出玻璃球冠的光线相对于入射光线的偏角β为β=180°-∠ENO=150°。
17.(2018·抚顺模拟)如图所示,空气中有一折射率为的玻璃柱体,其横截面是圆心角为90°、半径为R的扇形OAB。一束平行光平行于横截面,以45°入射角照射到OA上,OB不透光。若只考虑首次入射到圆弧AB上的光,则AB上有光透出部分的弧长为多长?
答案 πR
解析 由sinC=,可知光在玻璃柱中发生全反射的临界角C=45°,=,
所有光线从AO进入玻璃柱后的折射角均为r=30°,
从O点入射后的折射光线将沿半径从C点射出,假设从E点入射的光线经折射后到达D点时刚好发生全反射,
则∠ODE=45°。
如图所示,由几何关系可知θ=45°,
故AB上有光透出部分的弧长为πR。
相关资料
更多








