新高考数学一轮复习讲练测第04讲 直线、平面垂直的判定与性质（五大题型）（讲义）（2份，原卷版+解析版）

这是一份新高考数学一轮复习讲练测第04讲 直线、平面垂直的判定与性质（五大题型）（讲义）（2份，原卷版+解析版），文件包含新高考数学一轮复习讲练测第04讲直线平面垂直的判定与性质五大题型讲义原卷版doc、新高考数学一轮复习讲练测第04讲直线平面垂直的判定与性质五大题型讲义解析版doc等2份试卷配套教学资源，其中试卷共57页， 欢迎下载使用。

知识点1：直线与平面垂直的定义
如果一条直线和这个平面内的任意一条直线都垂直，那称这条直线和这个平面相互垂直．
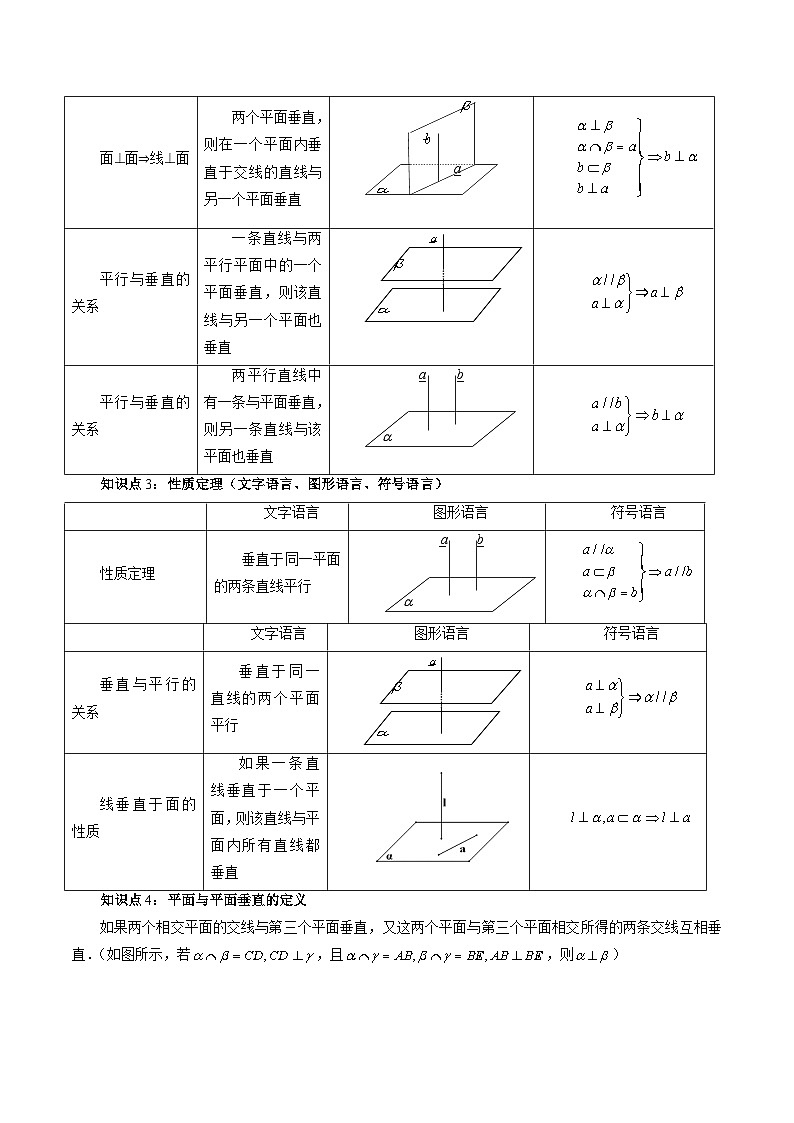
知识点2：判定定理（文字语言、图形语言、符号语言）
知识点3：性质定理（文字语言、图形语言、符号语言）
知识点4：平面与平面垂直的定义
如果两个相交平面的交线与第三个平面垂直，又这两个平面与第三个平面相交所得的两条交线互相垂直．（如图所示，若，且，则）
一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．
知识点5：判定定理（文字语言、图形语言、符号语言）
知识点6：性质定理（文字语言、图形语言、符号语言）
【解题方法总结】
线线线面面面
（1）证明线线垂直的方法
①等腰三角形底边上的中线是高；
②勾股定理逆定理；
③菱形对角线互相垂直；
④直径所对的圆周角是直角；
⑤向量的数量积为零；
⑥线面垂直的性质；
⑦平行线垂直直线的传递性（）．
（2）证明线面垂直的方法
①线面垂直的定义；
②线面垂直的判定（）；
③面面垂直的性质（）；
平行线垂直平面的传递性（）；
⑤面面垂直的性质（）．
（3）证明面面垂直的方法
①面面垂直的定义；
②面面垂直的判定定理（）．
空间中的线面平行、垂直的位置关系结构图如图所示，由图可知，线面垂直在所有关系中处于核心位置．
性质
性质
性质
性质
性质
判定
判定
判定
判定
判定
线∥面
线∥线
面∥面
线⊥面
线⊥线
面⊥面
题型一：垂直性质的简单判定
例1．（2023·甘肃兰州·校考模拟预测）设是两条不同的直线，是两个不同的平面，则下列说法正确的是（）
A．若，则
B．若，则
C．若，则
D．若，则
例2．（2023·重庆·统考模拟预测）已知l，m，n表示不同的直线，，，表示不同的平面，则下列四个命题正确的是（）
A．若，且，则B．若，，，则
C．若，且，则D．若，，，则
例3．（2023·陕西咸阳·统考二模）已知，是两条不同的直线，，是两个不同的平面，有以下四个命题：
①若∥，，则∥， ②若，，则，
③若，，则∥， ④若，，，则
其中正确的命题是（）
A．②③B．②④C．①③D．①②
变式1．（2023·河南·校联考模拟预测）已知是两个不同的平面，是两条不同的直线，则下列命题中正确的是（）
A．若，则B．若，则
C．若，则D．若，则
变式2．（2023·陕西咸阳·统考模拟预测）如图所示的菱形中，对角线交于点，将沿折到位置，使平面平面.以下命题:
①；
②平面平面；
③平面平面；
④三棱锥体积为.
其中正确命题序号为（ ）
A．①②③B．②③C．③④D．①②④
变式3．（2023·广西南宁·武鸣县武鸣中学校考三模）已知l，m，n是三条不同的直线，，是不同的平面，则下列条件中能推出的是（）
A．，，且
B．，，，且，
C．，，，且
D．，，且
【解题方法总结】
此类问题可以转化为一个正方体的棱、面等，进而进行排除．
题型二：证明线线垂直
例4．（2023·贵州黔东南·凯里一中校考模拟预测）如图，在三棱柱中，，．
证明：；
例5．（2023·广东深圳·统考二模）如图，在四棱锥中，底面为矩形，平面，点是的中点.
证明：；
例6．（2023·河南·校联考模拟预测）已知三棱柱中，是的中点，是线段上一点.
求证：；
变式4．（2023·福建宁德·校考模拟预测）图1是由直角梯形ABCD和以CD为直径的半圆组成的平面图形，，，．E是半圆上的一个动点，当△CDE周长最大时，将半圆沿着CD折起，使平面平面ABCD，此时的点E到达点P的位置，如图2．
求证：；
变式5．（2023·河南·校联考模拟预测）如图，已知三棱柱中，，，，是的中点，是线段上一点.
(1)求证：；
(2)设是棱上的动点（不包括边界），当的面积最小时，求棱锥的体积.
变式6．（2023·贵州毕节·校考模拟预测）在梯形中，，，，，如图1.沿对角线将折起，使点到达点的位置，为的中点，如图2.
证明：.
【解题方法总结】
题型三：证明线面垂直
(1)求证：平面；
(2)求四棱锥的体积.
例7．（2023·云南·校联考模拟预测）如图，在四棱锥中，已知，.
(1)证明：平面；
例8．（2023·云南昭通·校联考模拟预测）如图，在三棱锥中，平面ABD，E为AB的中点，，.
(1)证明：平面CED；
例9．（2023·内蒙古赤峰·赤峰二中校联考模拟预测）如图1，在五边形中，四边形为正方形，，，如图2，将沿折起，使得A至处，且．
(1)证明：平面；
变式7．（2023·重庆巴南·统考一模）如图所示，在三棱锥中，已知平面，平面平面．
(1)证明：平面；
变式8．（2023·广东广州·统考三模）如图，在几何体中，矩形所在平面与平面互相垂直，且，，．
(1)求证：平面；
变式9．（2023·天津津南·天津市咸水沽第一中学校考模拟预测）如图，在三棱柱中，平面平面，是的中点，且.
(1)证明：平面；
【解题方法总结】
垂直关系中线面垂直是重点．
线垂面哪里找
线垂面有何用
证明线面垂直常用两种方法．
方法一：线面垂直的判定．
线线垂直线面垂直，符号表示为：，那么．
方法二：面面垂直的性质．
面面垂直线面垂直，符号表示为：，那么．
题型四：证明面面垂直
例10．（2023·山西运城·山西省运城中学校校考二模）如图，在三棱柱中，侧面为菱形，，，.
(1)证明：平面平面；
例11．（2023·贵州贵阳·校联考三模）如图所示，在四棱锥中，底面为直角梯形，，，，，，.
(1)求证：平面平面；
例12．（2023·西藏日喀则·统考一模）如图，已知直角梯形与，，，，AD⊥AB，，G是线段上一点.
(1)平面⊥平面ABF
变式10．（2023·广东梅州·统考三模）如图所示，在几何体中，平面，点在平面的投影在线段上，，，，平面.
(1)证明：平面平面.
变式11．（2023·河北张家口·统考三模）如图，在三棱柱中，侧面为菱形，.
(1)证明：平面平面；
变式12．（2023·陕西西安·西安市大明宫中学校考模拟预测）如图，在长方体中，为棱的中点．
(1)证明：平面平面；
(2)画出平面与平面的交线，并说明理由；
(3)求过三点的平面将四棱柱分成的上、下两部分的体积之比．
变式13．（2023·云南·云南师大附中校考模拟预测）如图，为圆锥的顶点，A，为底面圆上两点，，为中点，点在线段上，且.
(1)证明：平面平面；
变式14．（2023·江苏南京·南京市第一中学校考模拟预测）在如图所示的空间几何体中，与均是等边三角形，直线平面，直线平面，.
(1)求证：平面平面；
【解题方法总结】
主要证明方法是利用面面垂直的判定定理（线面垂直面面垂直）．证明时，先从现有的直线中寻找平面的垂线，若图中不存在这样的直线，则可通过作辅助线来解决．
题型五：垂直关系的综合应用
例13．（2023·贵州铜仁·统考二模）如图，在直三棱柱中，，．
(1)试在平面内确定一点H，使得平面，并写出证明过程；
例14．（2023·全国·校联考模拟预测）如图，在正三棱柱（侧棱垂直于底面，且底面三角形是等边三角形）中，，、、分别是，，的中点．
(1)求证：平面平面；
(2)在线段上是否存在一点使平面？若存在，确定点的位置；若不存在，也请说明理由．
例15．（2023·天津·耀华中学校考二模）如图，在三棱锥A﹣BCD中，顶点A在底面BCD上的射影O在棱BD上，AB＝AD＝，BC＝BD＝2，∠CBD＝90°，E为CD的中点．
（1）求证：AD⊥平面ABC；
（2）求二面角B﹣AE﹣C的余弦值；
（3）已知P是平面ABD内一点，点Q为AE中点，且PQ⊥平面ABE，求线段PQ的长．
变式15．（2023·全国·校联考模拟预测）如图，在正方体中，，.
（1）求证：；
（2）在线段上，是否存在点，使得平面？并说明理由.
变式16．（2023·江西赣州·统考模拟预测）如图，在三棱柱中，侧面是矩形，侧面是菱形，，、分别为棱、的中点，为线段的中点.
(1)证明：平面；
(2)在棱上是否存在一点，使平面平面？若存在，请指出点的位置，并证明你的结论；若不存在，请说明理由.
变式17．（2023·安徽淮北·统考一模）如图，已知四棱锥的底面是平行四边形，侧面PAB是等边三角形，，，．
(1)求证：面面ABCD；
(2)设Q为侧棱PD上一点，四边形BEQF是过B，Q两点的截面，且平面BEQF，是否存在点Q，使得平面平面PAD？若存在，确定点Q的位置；若不存在，说明理由．
变式18．（2023·河北邯郸·统考二模）如图，直三棱柱ABC­A1B1C1中，D，E分别是棱BC，AB的中点，点F在棱CC1上，已知AB＝AC，AA1＝3，BC＝CF＝2．
（1）求证：C1E平面ADF；
（2）设点M在棱BB1上，当BM为何值时，平面CAM⊥平面ADF．
【解题方法总结】
（1）三种垂直的综合问题，一般通过作辅助线进行线线、线面、面面垂直间的转化．
（2）对于线面关系中的存在性问题，首先假设存在，然后在该假设条件下，利用线面关系的相关定理、性质进行推理论证．
1．（2022•乙卷（文））在正方体中，，分别为，的中点，则
A．平面平面B．平面平面
C．平面平面D．平面平面
2．（2021•浙江）如图，已知正方体，，分别是，的中点，则
A．直线与直线垂直，直线平面
B．直线与直线平行，直线平面
C．直线与直线相交，直线平面
D．直线与直线异面，直线平面
3．（多选题）（2021•新高考Ⅱ）如图，下列正方体中，为底面的中心，为所在棱的中点，，为正方体的顶点，则满足的是
A．B．
C．D．
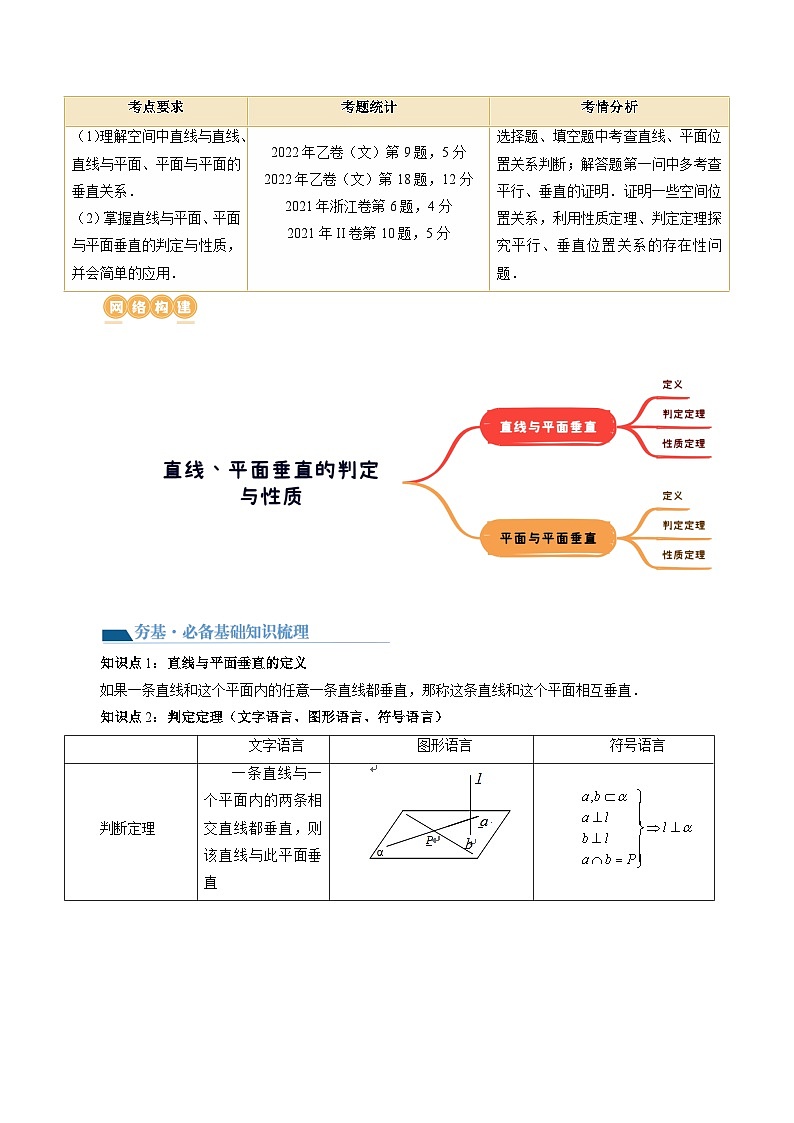
考点要求
考题统计
考情分析
（1）理解空间中直线与直线、直线与平面、平面与平面的垂直关系．
（2）掌握直线与平面、平面与平面垂直的判定与性质，并会简单的应用．
2022年乙卷（文）第9题，5分
2022年乙卷（文）第18题，12分
2021年浙江卷第6题，4分
2021年II卷第10题，5分
选择题、填空题中考查直线、平面位置关系判断；解答题第一问中多考查平行、垂直的证明．证明一些空间位置关系，利用性质定理、判定定理探究平行、垂直位置关系的存在性问题．
文字语言
图形语言
符号语言
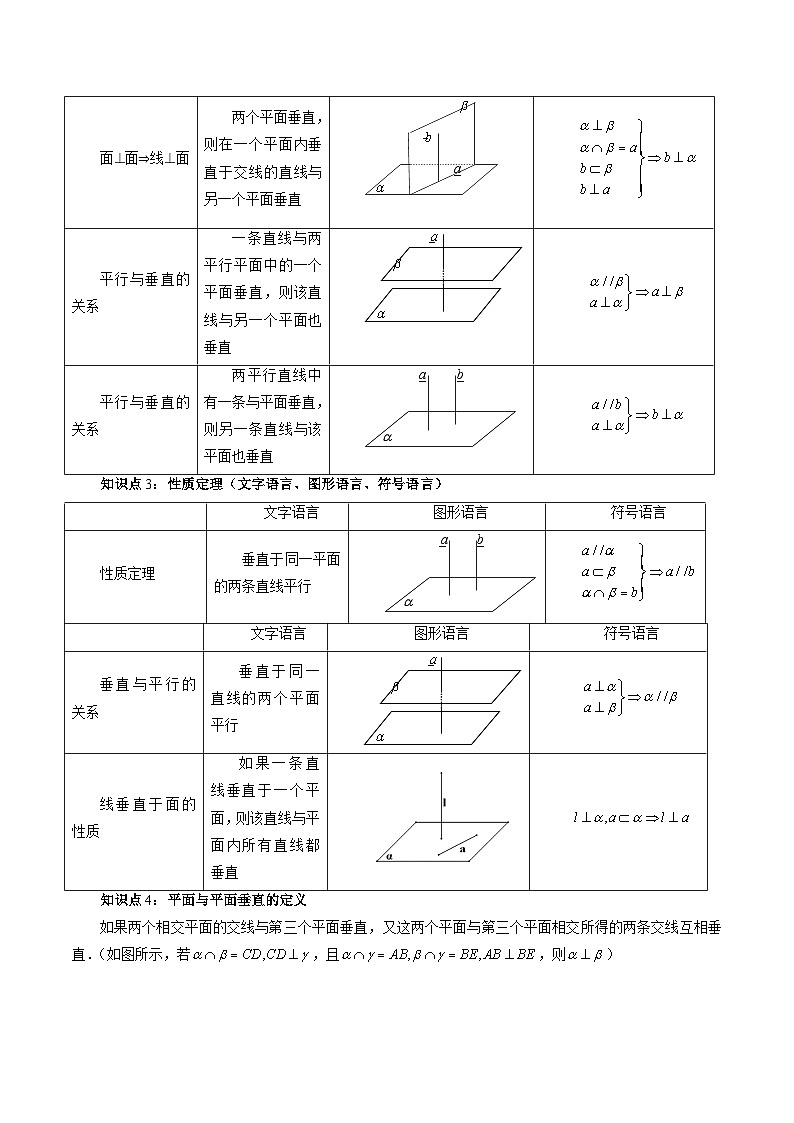
判断定理
一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直
面⊥面⇒线⊥面
两个平面垂直，则在一个平面内垂直于交线的直线与另一个平面垂直
_
_
a
平行与垂直的关系
一条直线与两平行平面中的一个平面垂直，则该直线与另一个平面也垂直
_
平行与垂直的关系
两平行直线中有一条与平面垂直，则另一条直线与该平面也垂直

_
b
_
a
文字语言
图形语言
符号语言
性质定理
垂直于同一平面的两条直线平行

_
b
_
a
文字语言
图形语言
符号语言
垂直与平行的关系
垂直于同一直线的两个平面平行
_
线垂直于面的性质
如果一条直线垂直于一个平面，则该直线与平面内所有直线都垂直
文字语言
图形语言
符号语言
判定定理
一个平面过另一个平面的垂线，则这两个平面垂直
_
文字语言
图形语言
符号语言
性质定理
两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直
_
_
a