浙教版（2024）七年级下册（2024）1.1 直线的相交练习

这是一份浙教版（2024）七年级下册（2024）1.1 直线的相交练习，共7页。
1． 下列生活、生产现象中，可以用基本事实“两点之间线段最短”来解释的是（ ）
A．用两个钉子就可以把木条固定在墙上
B．把弯曲的河道改直，可以缩短航程
C．利用圆规可以比较两条线段的大小关系
D．测量运动员的跳远成绩时，皮尺与起跳线保持垂直
2．如图所示，小明的家在P处，他想尽快赶到附近公路边搭顺风车，他选择P→C路线，用几何知识解释其道理正确的是（ ）
A．两点确定一条直线B．垂线段最短
C．两点之间线段最短D．经过一点有无数条直线
3．下列各图中，∠1和∠2是对顶角的是（ ）
A．B．
C．D．
4．以下奥运会比赛项目中，按点到直线的距离来评定成绩的是（ ）
A．跳远B．链球C．铅球D．铁饼
5．如图，直线AB和CD相交于点O，OE⊥OC，若∠AOC=58°，则∠EOB的大小为( )
A．29°B．32°C．45°D．58°
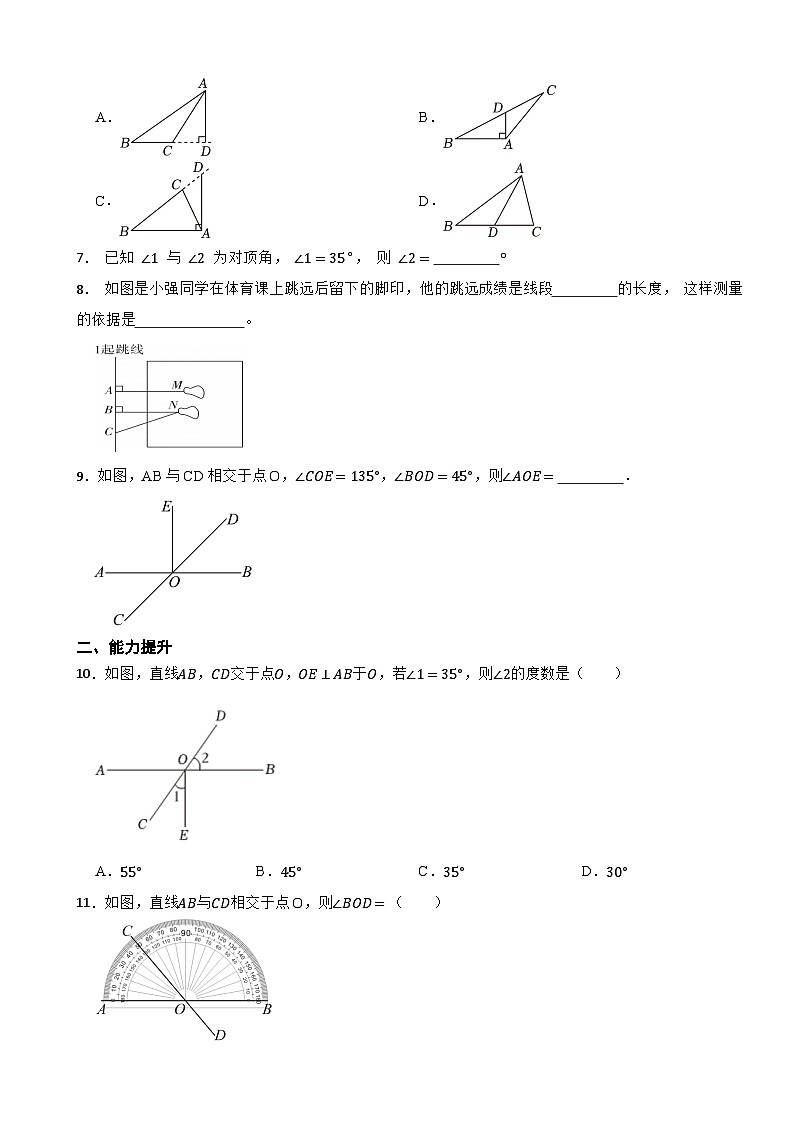
6． 下列图形中，线段AD的长表示点A到直线BC距离的是（ ）
A．B．
C．D．
7． 已知 ∠1 与 ∠2 为对顶角， ∠1=35∘， 则 ∠2= °
8． 如图是小强同学在体育课上跳远后留下的脚印， 他的跳远成绩是线段 的长度， 这样测量的依据是 。
9．如图，AB与CD相交于点O，∠COE=135°，∠BOD=45°，则∠AOE= ．
二、能力提升
10．如图，直线AB，CD交于点O，OE⊥AB于O，若∠1=35°，则∠2的度数是（ ）
A．55°B．45°C．35°D．30°
11．如图，直线AB与CD相交于点O，则∠BOD=（ ）
A．40°B．50°C．55°D．60°
12．已知：OA⊥OC，∠AOB：∠AOC=2：3．则∠BOC的度数为 ．
13．直线AB与直线CD相交于点O，过点O作射线OM垂直于CD，已知∠COB=30°，则∠AOM= ．
14．如图，直线AB，CD相交于点O，OM⊥AB，ON⊥CD.
（1）写出图中所有与∠AOC互余的角.
（2）当∠MON=120°时，求∠BOD 的度数.
15．如图，直线AB，CD相交于点O，.∠AOC=72°,射线OE在∠BOD的内部，∠DOE=2∠BOE.
（1）求∠BOE和∠AOE的度数.
（2）若射线OF与OE互相垂直，请直接写出∠DOF的度数.
三、拓展创新
16．如图，直线AB，CD相交于点O，OC平分∠BOE，∠AOE＝2∠FOD．
（1）若∠FOD＝21°，求∠AOD的度数；
（2）猜想OE与OF的位置关系，并说明理由．
17．如图，直线AB相与CD相交于O，OF，OD分别是∠AOE，∠BOE平分线．
（1）写出∠DOE的两个补角：
（2）若∠DOE=30°．求∠BOC和∠EOF的度数；
（3）试问射线OD与OF之间有什么特殊的位置关系？为什么？
答案解析部分
1．【答案】B
2．【答案】B
3．【答案】B
4．【答案】A
5．【答案】B
6．【答案】A
7．【答案】35
8．【答案】BN；垂线段最短
9．【答案】90°
10．【答案】A
11．【答案】B
12．【答案】30°或150°
13．【答案】60°或120°
14．【答案】（1）∵OM⊥AB，ON⊥CD，
∴∠AOM=∠CON=90°，
∴∠AOC+∠COM=90°，∠AOC+∠AON=90°，
∴与∠AOC互余的角为：∠COM，∠AON
（2）∵∠MON=120°，∠AOM=90°，
∴∠AON=∠MON-∠AOM=30°，
∵ON⊥CD，
∴∠NOD=90°，
∴∠BOD=180-∠AON-∠NOD=60°
15．【答案】（1）解：∵∠AOC=72°，
∴∠BOD=72°，∠AOD=108°，
设∠BOE=x，则∠DOE=2x，
由题意得x+2x=72°，
解得x=24°，
∴∠BOE=24°，∠DOE=48°，
∴∠AOE=156°.
（2）解：若射线OF在∠BOC的内部，
∠DOF=90°+48°=138°;
若射线OF在∠AOD的内部，
∠DOF=90°−48°=42°.
∴∠DOF的度数是138°或42°.
16．【答案】（1）解：∵∠FOD=21°，∠AOE=2∠FOD，∴∠AOE=42°，∴∠BOE=180°-∠AOE=180°-42°=138°.
∵OC平分∠BOE，∴∠BOC=-12∠BOE=-12×138°=69°，∴∠AOD=∠BOC=69°；
（2）解：猜想OE⊥OF，理由如下：
设∠DOF=x，则∠AOE=2x.
∴∠BOE=180°-2x.
∵OC平分∠BOE，
∴∠BOC=12180°−2x=90°−x.
∴∠AOD=∠BOC=90°-x.
∴∠AOF=∠AOD-∠DOF=90°-2x.
∴∠EOF=∠AOE+∠AOF=2x+90°-2x=90°.
∴OE⊥OF.
17．【答案】（1）解：∠DOE 的补角为：∠COE，∠AOD，∠BOC．
（2）解：∵OD是∠BOE 的平分线，
∴∠DOE=∠BOD=30°，∠BOE＝60°；
∵∠BOC＝180°﹣∠BOD，
∴∠BOC＝150°；
∵∠AOE＝180°﹣∠BOE，
∴∠AOE＝120°；
又∵OF是∠AOE 的平分线，
∴∠EOF=12∠AOE＝60°
（3）解：射线OD与OF互相垂直．理由如下：
∵OF，OD分别是∠AOE，∠BOE的平分线，
∴∠DOF＝∠DOE+∠EOF＝12∠BOE+12∠EOA＝12（∠BOE+∠EOA）＝12×180°＝90°．
∴OD⊥OF．
即射线OD、OF的位置关系是垂直．