中考数学第二轮复习专题练习压轴题01 二次函数图象性质与几何问题（3题型+2类型+解题模板+技巧精讲）（原卷版）

这是一份中考数学第二轮复习专题练习压轴题01 二次函数图象性质与几何问题（3题型+2类型+解题模板+技巧精讲）（原卷版），共17页。

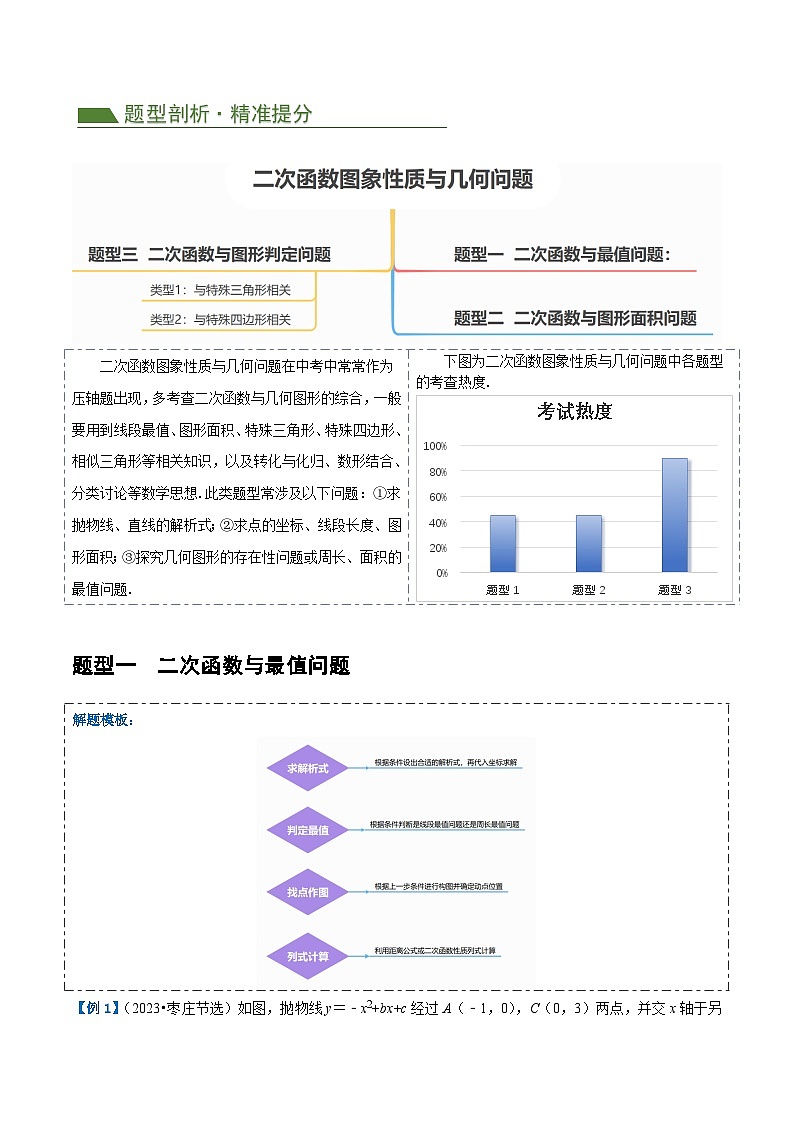
TOC \ "1-2" \n \p " " \h \z \u \l "_Tc157701139" 题型一 二次函数与最值问题：
\l "_Tc157701140" 题型二 二次函数与图形面积问题
\l "_Tc157701141" 题型三 二次函数与图形判定问题
\l "_Tc157701142" 类型1：与特殊三角形相关
\l "_Tc157701143" 类型2：与特殊四边形相关
题型一 二次函数与最值问题
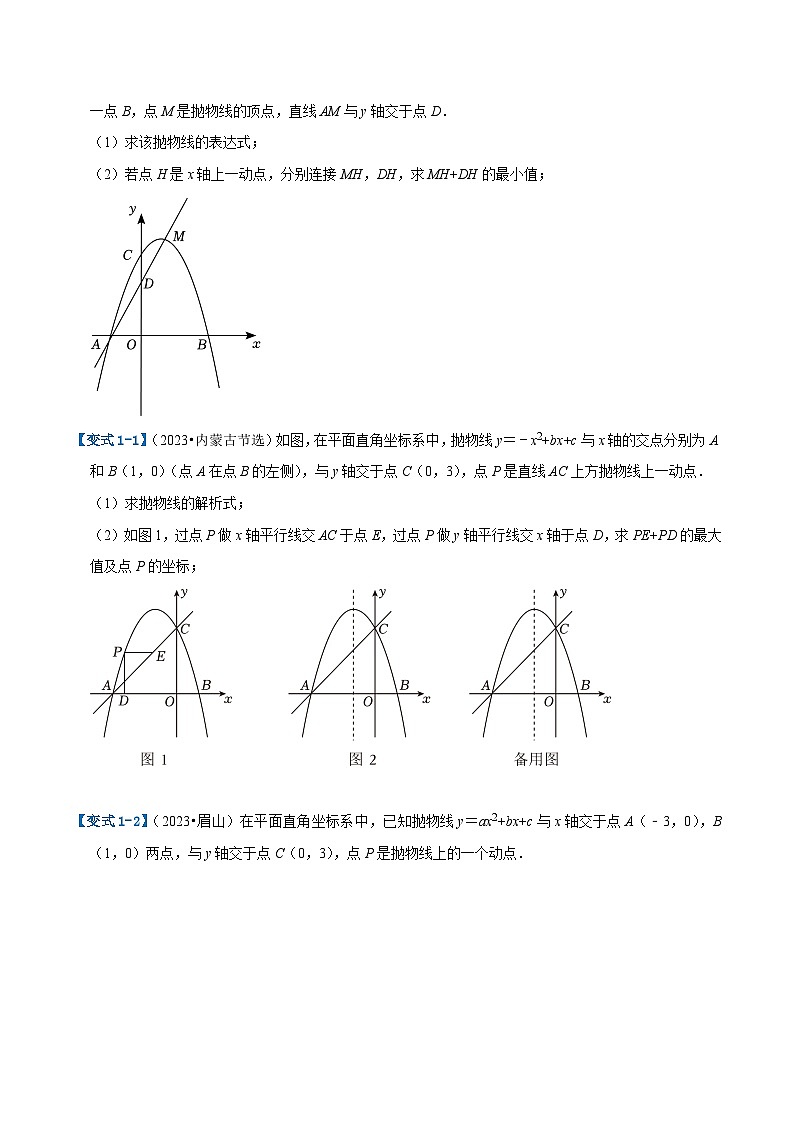
【例1】（2023•枣庄节选）如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），C（0，3）两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与y轴交于点D．
（1）求该抛物线的表达式；
（2）若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；
【变式1-1】（2023•内蒙古节选）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴的交点分别为A和B（1，0）（点A在点B的左侧），与y轴交于点C（0，3），点P是直线AC上方抛物线上一动点．
（1）求抛物线的解析式；
（2）如图1，过点P做x轴平行线交AC于点E，过点P做y轴平行线交x轴于点D，求PE+PD的最大值及点P的坐标；
【变式1-2】（2023•眉山）在平面直角坐标系中，已知抛物线y＝ax2+bx+c与x轴交于点A（﹣3，0），B（1，0）两点，与y轴交于点C（0，3），点P是抛物线上的一个动点．
（1）求抛物线的表达式；
（2）当点P在直线AC上方的抛物线上时，连接BP交AC于点D，如图1，当的值最大时，求点P的坐标及的最大值；
【变式1-3】（2023•西宁）如图，在平面直角坐标系中，直线l与x轴交于点A（6，0），与y轴交于点B（0，﹣6），抛物线经过点A，B，且对称轴是直线x＝1．
（1）求直线l的解析式；
（2）求抛物线的解析式；
（3）点P是直线l下方抛物线上的一动点，过点P作PC⊥x轴，垂足为C，交直线1于点D，过点P作PM⊥l，垂足为M．求PM的最大值及此时P点的坐标．
题型二 二次函数与图形面积问题
【例2】（2023•娄底）如图，抛物线y＝x2+bx+c过点A（﹣1，0）、点B（5，0），交y轴于点C．
（1）求b，c的值．
（2）点P（x0，y0）（0＜x0＜5）是抛物线上的动点．当x0取何值时，△PBC的面积最大？并求出△PBC面积的最大值；
【变式2-1】（2023•怀化）如图一所示，在平面直角坐标系中，抛物线y＝ax2+bx﹣8与x轴交于A（﹣4，0）、B（2，0）两点，与y轴交于点C．
（1）求抛物线的函数表达式及顶点坐标；
（2）点P为第三象限内抛物线上一点，作直线AC，连接PA、PC，求△PAC面积的最大值及此时点P的坐标；
【变式2-2】（2023•安徽）在平面直角坐标系中，点O是坐标原点，抛物线y＝ax2+bx（a≠0）经过点A（3，3），对称轴为直线x＝2．
（1）求a，b的值；
（2）已知点B，C在抛物线上，点B的横坐标为t，点C的横坐标为t+1．过点B作x轴的垂线交直线OA于点D，过点C作x轴的垂线交直线OA于点E．
（i）当0＜t＜2时，求△OBD与△ACE的面积之和；
（ii）在抛物线对称轴右侧，是否存在点B，使得以B，C，D，E为顶点的四边形的面积为？若存在，请求出点B的横坐标t的值；若不存在，请说明理由．
【变式2-3】（2023·辽宁阜新·统考中考真题）如图，在平面直角坐标系中，二次函数的图象与轴交于点和点，与y轴交于点C．

(1)求这个二次函数的表达式．
(2)如图1，二次函数图象的对称轴与直线交于点D，若点M是直线上方抛物线上的一个动点，求面积的最大值．
【变式2-4】（2023·湖南·统考中考真题）如图，二次函数的图象与轴交于，两点，与轴交于点，其中，．

(1)求这个二次函数的表达式；
(2)在二次函数图象上是否存在点，使得？若存在，请求出点坐标；若不存在，请说明理由；
题型三 二次函数与图形判定问题
类型一 与特殊三角形相关
【例3】（2023•随州节选）如图1，平面直角坐标系xOy中，抛物线y＝ax2+bx+c过点A（﹣1，0），B（2，0）和C（0，2），连接BC，点P（m，n）（m＞0）为抛物线上一动点，过点P作PN⊥x轴交直线BC于点M，交x轴于点N．
（1）直接写出抛物线和直线BC的解析式；
（2）如图2，连接OM，当△OCM为等腰三角形时，求m的值；
【变式3-1】（2023•恩施州节选）在平面直角坐标系xOy中，O为坐标原点，已知抛物线y＝﹣x2+bx+c与y轴交于点A，抛物线的对称轴与x轴交于点B．
（1）如图，若A（0，），抛物线的对称轴为x＝3．求抛物线的解析式，并直接写出y≥时x的取值范围；
（2）在（1）的条件下，若P为y轴上的点，C为x轴上方抛物线上的点，当△PBC为等边三角形时，求点P，C的坐标；
【变式3-2】（2023•益阳）在平面直角坐标系xOy中，直线l：y＝a（x+2）（a＞0）与x轴交于点A，与抛物线E：y＝ax2交于B，C两点（B在C的左边）．
（1）求A点的坐标；
（2）如图1，若B点关于x轴的对称点为B′点，当以点A，B′，C为顶点的三角形是直角三角形时，求实数a的值；
类型二 与特殊四边形相关
【例4】（2023•自贡）如图，抛物线y＝﹣x2+bx+4与x轴交于A（﹣3，0），B两点，与y轴交于点C．
（1）求抛物线解析式及B，C两点坐标；
（2）以A，B，C，D为顶点的四边形是平行四边形，求点D坐标；
【变式4-1】（2023•巴中）在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）经过点A（﹣1，0）和B（0，3），其顶点的横坐标为1．
（1）求抛物线的表达式．
（2）若直线x＝m与x轴交于点N，在第一象限内与抛物线交于点M，当m取何值时，使得AN+MN有最大值，并求出最大值．
（3）若点P为抛物线y＝ax2+bx+c（a≠0）的对称轴上一动点，将抛物线向左平移1个单位长度后，Q为平移后抛物线上一动点．在（2）的条件下求得的点M，是否能与A、P、Q构成平行四边形？若能构成，求出Q点坐标；若不能构成，请说明理由．
【变式4-2】（2023•锦州）如图，抛物线y＝﹣x2+bx+c交x轴于点A（﹣1，0）和B，交y轴于点C（0，3），顶点为D．
（1）求抛物线的表达式；
（2）若点E在第一象限内对称轴右侧的抛物线上，四边形ODEB的面积为7，求点E的坐标；
（3）在（2）的条件下，若点F是对称轴上一点，点H是坐标平面内一点，在对称轴右侧的抛物线上是否存在点G，使以点E，F，G，H为顶点的四边形是菱形，且∠EFG＝60°，如果存在，请直接写出点G的坐标；如果不存在，请说明理由．
【变式4-3】（2022•黔西南州）如图，在平面直角坐标系中，经过点A（4，0）的直线AB与y轴交于点B（0，4）．经过原点O的抛物线y＝﹣x2+bx+c交直线AB于点A，C，抛物线的顶点为D．
（1）求抛物线y＝﹣x2+bx+c的表达式；
（2）M是线段AB上一点，N是抛物线上一点，当MN∥y轴且MN＝2时，求点M的坐标；
（3）P是抛物线上一动点，Q是平面直角坐标系内一点．是否存在以点A，C，P，Q为顶点的四边形是矩形？若存在，直接写出点Q的坐标；若不存在，请说明理由．
一、解答题
1．（2023·辽宁·统考中考真题）如图，抛物线y=ax2+83x+c与x轴交于点A和点B3.0，与y轴交于点C0,4，点P为第一象限内抛物线上的动点过点P作PE⊥x轴于点E，交BC于点F．

(1)求抛物线的解析式；
(2)当△BEF的周长是线段PF长度的2倍时，求点P的坐标；
(3)当点P运动到抛物线顶点时，点Q是y轴上的动点，连接BQ，过点B作直线l⊥BQ，连接QF并延长交直线l于点M．当BQ=BM时，请直接写出点的坐标．
2．（2023·湖南张家界·统考中考真题）如图，在平面直角坐标系中，已知二次函数y=ax2+bx+c的图象与x轴交于点A-2,0和点B6,0两点，与y轴交于点C0,6．点D为线段BC上的一动点．

(1)求二次函数的表达式；
(2)如图1，求△AOD周长的最小值；
(3)如图2，过动点D作DP∥AC交抛物线第一象限部分于点P，连接PA,PB，记△PAD与△PBD的面积和为S，当S取得最大值时，求点P的坐标，并求出此时S的最大值．
3．（2023·四川凉山·统考中考真题）如图，已知抛物线与x轴交于A1,0和B-5,0两点，与y轴交于点C．直线y=-3x+3过抛物线的顶点P．
(1)求抛物线的函数解析式；
(2)若直线x=m-5