四川省成都市第十二中学2024-2025学年七年级上学期12月考 数学试卷（含解析）

这是一份四川省成都市第十二中学2024-2025学年七年级上学期12月考 数学试卷（含解析），共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．如果水位升高0.6 m时水位变化记作，那么水位下降0.4m时水位变化记为( )
A．0.4 mB．0.6 mC．D．
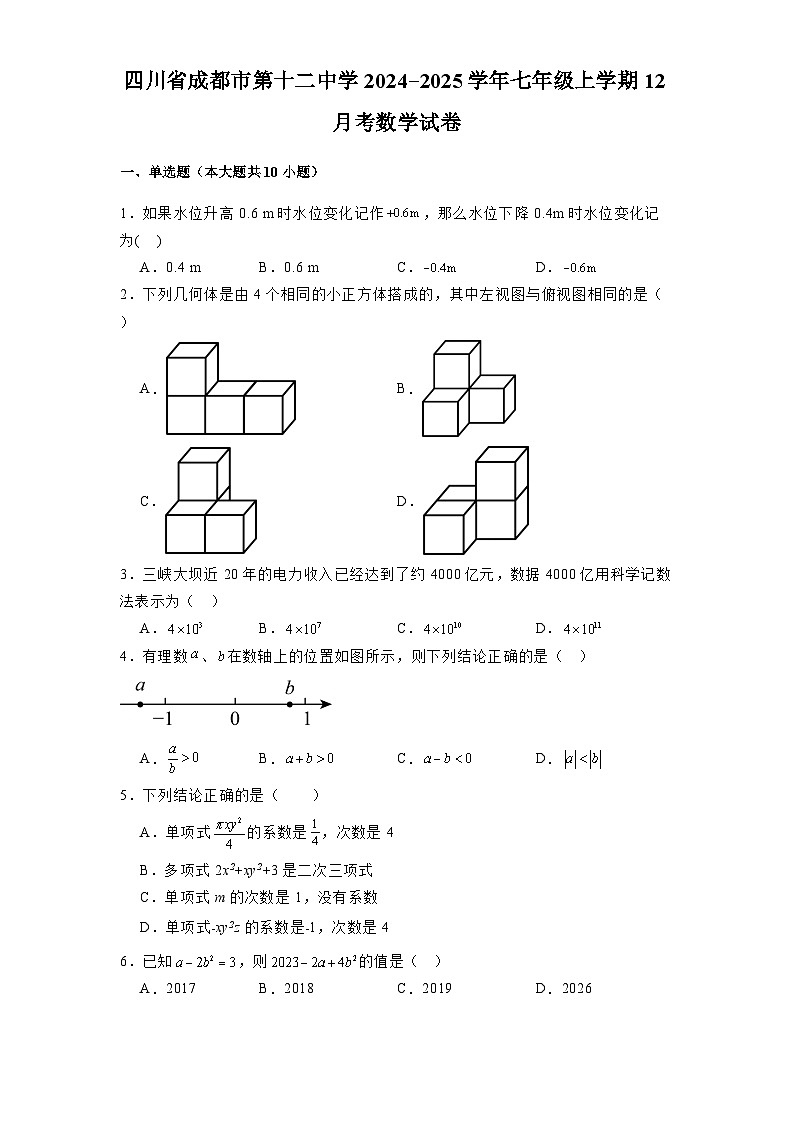
2．下列几何体是由4个相同的小正方体搭成的，其中左视图与俯视图相同的是（ ）
A．B．
C．D．
3．三峡大坝近20年的电力收入已经达到了约4000亿元，数据4000亿用科学记数法表示为（ ）
A．B．C．D．
4．有理数、在数轴上的位置如图所示，则下列结论正确的是（ ）
A．B．C．D．
5．下列结论正确的是（ ）
A．单项式的系数是，次数是4
B．多项式2x2+xy2+3是二次三项式
C．单项式m的次数是1，没有系数
D．单项式﹣xy2z的系数是﹣1，次数是4
6．已知，则的值是（ ）
A．2017B．2018C．2019D．2026
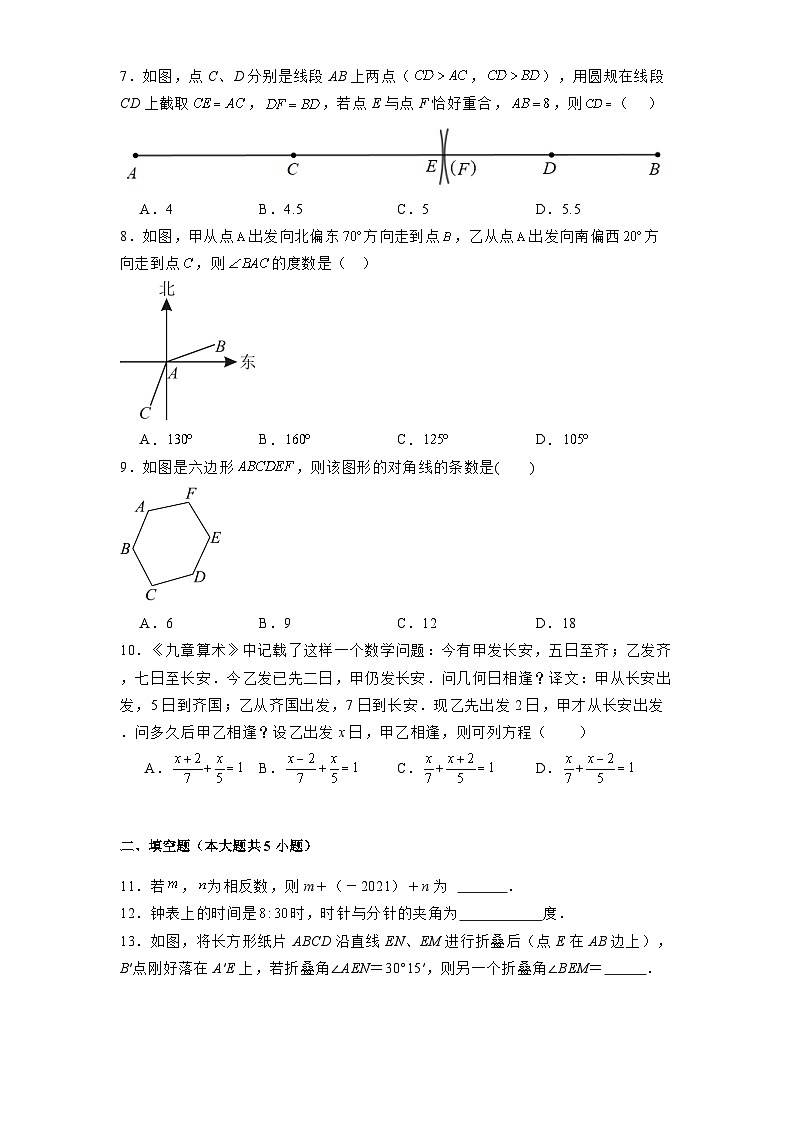
7．如图，点C、D分别是线段AB上两点（，），用圆规在线段CD上截取，，若点E与点F恰好重合，，则（ ）
A．4B．4.5C．5D．5.5
8．如图，甲从点出发向北偏东方向走到点，乙从点出发向南偏西方向走到点，则的度数是（ ）
A．B．C．D．
9．如图是六边形，则该图形的对角线的条数是( )
A．6B．9C．12D．18
10．《九章算术》中记载了这样一个数学问题：今有甲发长安，五日至齐；乙发齐，七日至长安．今乙发已先二日，甲仍发长安．问几何日相逢？译文：甲从长安出发，5日到齐国；乙从齐国出发，7日到长安．现乙先出发2日，甲才从长安出发．问多久后甲乙相逢？设乙出发x日，甲乙相逢，则可列方程（ ）
A．B．C．D．
二、填空题（本大题共5小题）
11．若，为相反数，则m＋（－2021）＋n为 ．
12．钟表上的时间是时，时针与分针的夹角为 度．
13．如图，将长方形纸片ABCD沿直线EN、EM进行折叠后（点E在AB边上），B′点刚好落在A′E上，若折叠角∠AEN＝30°15′，则另一个折叠角∠BEM＝ ．
14．完全相同的6个小长方形如图所示放置，形成了两边长分别为a，b的大长方形，则图中阴影部分的周长是 .(用含a，b的式子表示)
15．如图所示，将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为，第2幅图形中“●”的个数为，第3幅图形中“●”的个数为，…，以此类推，则的值为 ．
三、解答题（本大题共6小题）
16．计算或解方程．
(1)；
(2)．
17．已知．
(1)求；
(2)现有，当时，求的值．
18．对于有理数，定义了一种“”的新运算，具体为：．
(1)计算：①；②；
(2)若是关于的一元一次方程的解，求的值．
19．点为直线上一点，在直线同侧任作射线，使得．
(1)如图一，过点作射线，使为的角平分线．若时．则________，__________；
(2)如图二，过点作射线．当恰好为的角平分线时，另作射线．使得平分．
①若，求的度数（写出推理过程）；
②若，则的度数是_________（直接填空）；
20．为进一步推进“书香新区·全民阅读”建设，天府新区某社区书屋计划增订国学类图书100本，科学类图书x本．其现有甲乙两家图书店参与竞标，两家书店的竞标方案如下：
(1)请用含的代数式分别表示到甲乙两家图书店购买的费用；
(2)已知该社区书屋原有藏书2000册，本社区有常住居民1500户，该书屋想要图书量与居民户数比达到，计划拨出2000元经费采购这批图书，这批经费够吗？若够，应在哪家书店采购？若不够，请说明理由．
21．数形结合是数学中常用的思想方法，而数轴是数形结合法解决问题的有效工具．数轴上两点 A、B表示的数分别为a、b， 若， 则A、B 两点之间的距离， 例： 在数轴上点A 表示的数是5， 点B表示的数是15， 则A、B两点间的距离为．
定义： 在数轴上， 如果线段间从左往右的点将线段n等分，则这个点都叫做线段的 n等分点． 若是靠近A 的第1个 n等分点，则记为，是靠近A的第2个等分点， 则记为， ……．是靠近A的第个n等分点，则记为．，
探究一：
如图1，在数轴上两点A、B表示的数分别为a、b，若，则线段的二等分点表示的数为 ；
(1)探究二：如图2，在数轴上A、B两点表示的数分别为a、b，若（则线段上靠近点A的第2个五等分点表示的数为
(2)应用一：如图3，在数轴上两点A、B表示的数分别为 、 −2，则线段的距离为 ；数轴上两点C、D表示的数分别为 、4，则线段的距离为 ；若线段上靠近A的四等分点与线段上靠近C的十等分点（ 重合，请求出x的值．
(3)应用二：如图4，在数轴上A、B两点表示的数分别为和，若点 P从A点以每秒3个单位的速度向右移动，同时点 Q从B点以每秒2个单位的速度向左移动，当两点出发时间为 t秒时，线段上靠近A的等分点与线段的三等分点重合，请直接写出此时的t为
参考答案
1．【答案】C
【分析】首先根据题意，明确“正”和“负”所表示的意义，再根据题意作答即可．
【详解】解：如果水位升高0.6m时水位变化记作+0.6m，那么水位下降0.4m时水位变化记为-0.4m．
故此题答案为C．
2．【答案】C
【详解】从物体的前面向后面投射所得的视图称主视图（正视图）——能反映物体的前面形状；
从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状；
从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状．
选项C左视图与俯视图都是如下图所示：
故此题答案为C.
3．【答案】D
【分析】科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值时，n是正数；当原数的绝对值时，n是负数．
【详解】解：4000亿用科学记数法表示为：，
故此题答案为D．
4．【答案】C
【分析】根据数轴上的位置特点，可知，再根据有理数加法，减法，除法运算法则及绝对值的意义逐一判断即可得解．
【详解】解：根据数轴可得：，且，
∴，，，
观察四个选项，选项C符合题意．
故此题答案为C．
5．【答案】D
【分析】利用多项式和单项式相关定义进行解答．
【详解】A、单项式的系数是，次数是3，故原题说法错误；
B、多项式2x2+xy2+3是三次三项式，故原题说法错误；
C、单项式m的次数是1，系数为1，故原题说法错误；
D、单项式﹣xy2z的系数是﹣1，次数是4，故原题说法正确；
故此题答案为D．
6．【答案】A
【分析】将，整体代入多项式，进行计算即可．
【详解】解：∵，
∴；
故此题答案为A．
7．【答案】A
【分析】根据题意可得，，再由即可得到答案．
【详解】解：CE=AC，DF=BD，点E与点F恰好重合，
∴CE=AC，DE=BD，
∴，，
∴，
故此题答案为A．
8．【答案】A
【分析】根据方位角的定义，列算式求解即可．
【详解】解：由题意可得：，
故此题答案为A．
9．【答案】B
【分析】边形对角线的总条数为：（，且为整数），由此可得出答案．
【详解】解：六边形的对角线的条数．
故此题答案为B．
10．【答案】D
【分析】根据题意设乙出发x日，甲乙相逢，则甲、乙分别所走路程占总路程的和，进而得出等式．
【详解】解：设乙出发x日，甲乙相逢，则甲出发日，故可列方程为：
．
故此题答案为D．
11．【答案】-2021
【分析】根据相反数的意义得出，从而可计算m＋（－2021）＋n的值．
【详解】解：∵，为相反数，
∴，
∴m＋（－2021）＋n=0-2021=-2021
12．【答案】
【分析】利用时针与分针相距的份数乘以每份的度数．根据钟面平均分成12份，可得每份的度数，根据时针与分针相距的份数乘以每份的度数，可得答案．
【详解】解：钟面平均分成12份，每份30度，
时，时针指向和的中间，分针指向，则时针与分针相距份，
夹角为（度）
13．【答案】59°45′
【分析】由折叠的性质得∠A′EN=∠AEN=30°15′，∠BEM=∠A′EM，从而根据角的和差可求出∠BEA′的度数，进而可求出∠BEM的度数．
【详解】由折叠知，∠A′EN=∠AEN=30°15′，∠BEM=∠A′EM，
∴∠BEA′=180－30°15′－30°15′=119°30′，
∴∠BEM=∠A′EM=119°30′÷2=59°45′．
14．【答案】
【详解】解：设小长方形的长为x，宽为y（），根据图形可得，
，，
∴，
∴
，
∴图中阴影部分的周长是．
15．【答案】120
【分析】根据题意得出变化规律，再求出解即可．
【详解】解：根据题意，得；
；
，
∴．
∴．
16．【答案】(1)
(2)
【分析】（1）根据含乘方的有理数混合运算法则进行计算即可；
（2）先去分母、再去括号，然后移项合并同类项，最后系数化为1．
【详解】（1）解：
；
（2）解：，
去分母得：，
去括号得：，
移项，合并同类项得：，
系数化为1得：．
17．【答案】(1)
(2)
【分析】（1）根据，根据整式加减运算法则计算即可求出；
（2）根据可以得到C，然后将代入C，计算即可．
【详解】（1）解：∵，
∴
；
（2）解：∵，
∴，
；
∴，
∵，
∴．
18．【答案】(1)①；②−2
(2)
【分析】（1）①根据新定义运算法则列式计算即可；②根据新定义运算法则列式计算即可；
（2）根据新定义运算法则列方程计算即可．
【详解】（1）解：①，
，
②，
；
（2）解：分两种情况讨论：
①若，则，
解得；
②若，则，
解得；
不满足，
应舍去，
综上所述：的值为1．
19．【答案】(1)
(2)①；②
【分析】（1）根据图中角的和差关系和角平分线的定义求解；
（2）①根据角平分线的定义求出和，再根据求解；②同理①即可解答．
【详解】（1）解：∵，
，
平分，
，
；
（2）解：①
，
平分平分，
，
；
②，
，
平分平分，
，
．
20．【答案】(1)购买甲书店图书的费用为：元；购买乙书店图书的费用为：元；
(2)经费够，应在甲书店采购．
【分析】（1）根据题意列出代数式；
（2）先求得还需要科学类图书本，将x=150代入（1）中的代数式，即可求解．
【详解】（1）解：购买甲书店图书的费用为：元；
购买乙书店图书的费用为：元；
（2）还需要科学类图书：（本）．
在甲书店采购需要的费用为：（元），
在乙书店采购需要的费用为：（元）（元），
答：经费够，应在甲书店采购．
21．【答案】(1)
(2)8，10，2
(3)或
【分析】（1）根据两点间的距离公式，以及五等分点的含义，列出代数式即可；
（2）根据两点间的距离公式，求出，根据等分点的含义，列出方程进行求解即可；
（3）分在点左侧以及在点右侧两种情况，再分和重合以及和重合，两种情况，列出方程进行求解即可．
【详解】（1）解：由题意，得：表示的数为
（2），
由题意，得：，解得：x=2；
故答案为：8，10，2；
（3），
∴，
∵点 P从A点以每秒3个单位的速度向右移动，同时点 Q从B点以每秒2个单位的速度向左移动，
∴点表示的数为，点表示的数为，
当在点左侧时：，
∴，
当时，解得：；
当，解得：（不满足题意，舍去）；
当在点右侧时：，
∴，
当时，解得：（不满足题意，舍去）；
当，解得：；
综上：或．
甲书店
乙书店
报价：国学类15元/本，科学类8元/本
报价：国学类15元/本，科学类8元/本
优惠方案：一律打七折
优惠方案：买两本国学类图书，赠送一本科学类图书，总价在此基础上再优惠200元