2025高考数学一轮复习-第1章-集合与常用逻辑用语、不等式-第5讲 二次函数与一元二次方程、不等式【课件】

这是一份2025高考数学一轮复习-第1章-集合与常用逻辑用语、不等式-第5讲 二次函数与一元二次方程、不等式【课件】，共57页。PPT课件主要包含了教材再现四基诊断，aa≥0，重点串讲能力提升，一元二次不等式的解法，－21，x1＜x＜4，三个两次的关系，一元二次方程根的分布等内容，欢迎下载使用。
课程标准　1.会结合一元二次函数的图象判断一元二次方程根的个数，了解二次函数零点与一元二次方程根的关系．　2.会从实际情境中抽象出一元二次不等式．　3.能借助一元二次函数解一元二次不等式．4．能借助一元二次函数的图象，了解一元二次不等式与相应函数、方程的联系．
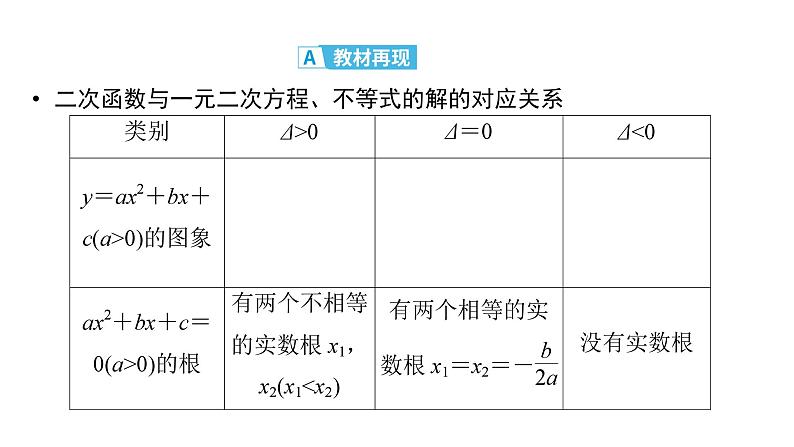
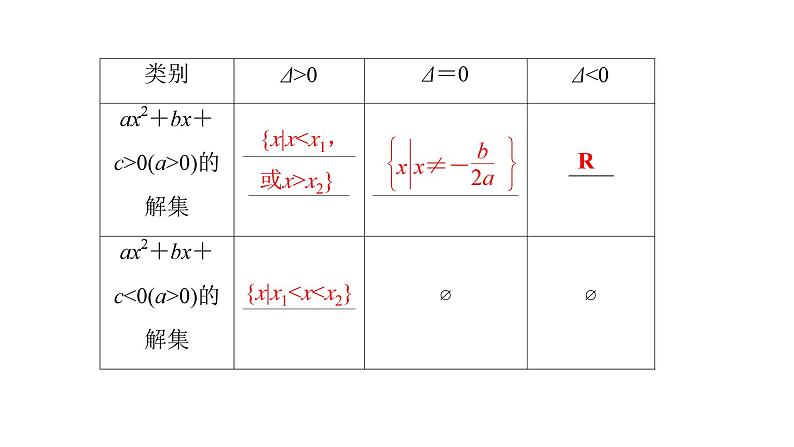
二次函数与一元二次方程、不等式的解的对应关系
{x|xx2}
{x|x10的解集的子集，可以先求解集，再由子集的含义求解参数的值（或范围）.(2)转化为函数值域问题，即已知函数f(x)的值域为[m，n]，则f(x)≥a恒成立⇒f(x)min≥a，即m≥a；f(x)≤a恒成立⇒f(x)max≤a，即n≤a.
(2024·河北石家庄质检)当－2≤x≤2时，不等式x2－mx＋1＞0恒成立，则实数m的取值范围为(　　)A．(－2，2) B．(－∞，－2)C．[－2，2] D．(2，＋∞)
角度3　给定参数范围的恒成立问题例6　已知关于x的不等式2x－1＞m(x2－1).(1)是否存在实数m，使不等式对任意x∈R恒成立，并说明理由；(2)若不等式对于m∈[－2，2]恒成立，求实数x的取值范围；(3)若不等式对于x∈(1，＋∞)恒成立，求m的取值范围．
[解]　(1)原不等式等价于mx2－2x＋(1－m)＜0，当m＝0时，－2x＋1＜0不恒成立；当m≠0时，若不等式对于任意实数x恒成立，则需m＜0且Δ＝4－4m(1－m)＜0，无解，所以不存在实数m，使不等式恒成立．
解决一元二次不等式中恒成立问题的方法解决恒成立问题一定要清楚选谁为主元，谁是参数．一般情况下，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数．即把变元与参数交换位置，构造以参数为变量的函数，根据原变量的取值范围列式求解．
已知a∈[－1，1]时，不等式x2＋(a－4)x＋4－2a＞0恒成立，则x的取值范围为　　　　　　　　　　．
(－∞，1)∪(3，＋∞)
例7　已知方程x2＋(m－2)x＋5－m＝0有两个不相等的实数根，且两个实数根都大于2，则实数m的取值范围是(　　)A．(－5，－4)∪(4，＋∞)B．(－5，＋∞)C．(－5，－4)D．(－4，－2)∪(4，＋∞)
关于一元二次方程根的分布问题主要利用三个二次关系，注意数形结合思想及根与系数关系的应用．