






中考数学考点选填题针对训练历年真题图形与点的坐标及圆的相关计算-中考数学第三轮专题复习课件
展开
这是一份中考数学考点选填题针对训练历年真题图形与点的坐标及圆的相关计算-中考数学第三轮专题复习课件,共29页。
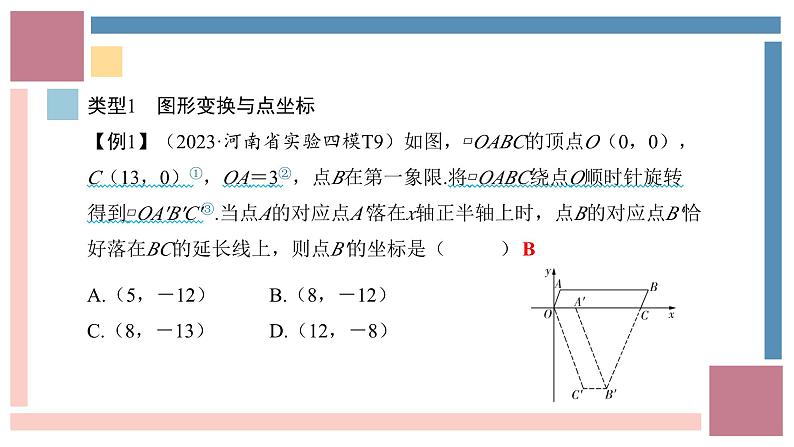
类型1 图形变换与点坐标【例1】(2023·河南省实验四模T9)如图,▱OABC的顶点O(0,0),C(13,0)①,OA=3②,点B在第一象限.将▱OABC绕点O顺时针旋转得到▱OA'B'C'③.当点A的对应点A'落在x轴正半轴上时,点B的对应点B'恰好落在BC的延长线上,则点B'的坐标是( B )
· 可视化思维·
作辅助线,结合条件得进一步结论
类型2 规律探究与点坐标【例2】(2023·洛阳三模T10)如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动一个单位长度①,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2 023的坐标为( A )
由条件①中的移动方法得点的坐标规律
1.(2023·南阳二模)如图,△OAB的顶点O(0,0),A(6,0),B(6,8),C是OB边的中点,过点C作CD⊥OB交x轴于点D.将△OCD沿x轴向右平移,当点C的对应点恰好落在AB边上时,此时点D的对应点的坐标为( A )
类型1 图形变换与点坐标
2.(2023·新乡三模)如图,已知点A(6,0),B(0,8),点P在y轴负半轴上.若将△PAB沿直线AP折叠,使点B的对应点恰好落在x轴正半轴上的点B'处,则点P的坐标是( B )
3.(2023·永城二模)如图,在平面直角坐标系xOy中,四边形OABC为矩形,点A,C分别在y轴,x轴上,且点B(4,3),点D为边BC上一点.将∠B沿AD所在直线翻折,当点B的对应点B'恰好落在对角线AC上时,点D的坐标为( B )
类型2 规律探究与点坐标
4.(2023·河南三模)风力发电是一种常见的绿色环保发电形式,它能够使大自然的资源得到更好地利用.如图1,风力发电机有三个底端重合、两两成120°角的叶片,以三个叶片的重合点为原点,水平方向为x轴建立平面直角坐标系(如图2所示).已知开始时其中一个叶片的外端点A的坐标为(5,5),在一段时间内,叶片每秒绕原点O顺时针转动90°,则第2 023秒时,点A的对应点A2 023的坐标为( B )
5.(2023·郑州外国语三模T10)规定:在平面直角坐标系中,一个点作“0”变换表示将它向右平移一个单位长度,一个点作“1”变换表示将它绕原点顺时针旋转90°,由数字0和1组成的序列表示一个点按照上面描述依次连续变换,例如:如图,点O(0,0)按序列“011…”作变换,表示点O先向右平移一个单位长度得到O1(1,0),再将O1(1,0)绕原点顺时针旋转90°得到O2(0,-1),再将O2(0,-1)绕原点顺时针旋转90° 得到O3(-1,0)…依次类推,点(0,1)经过“011011011”变换后得到的点的坐标为( A )
选填题重难点专题二 圆的相关计算
由锐角三角函数与勾股定理得基本结论
由题中条件及作辅助线得基本结论 ↓
由勾股定理、圆周角定理及其推论得进一步结论
类型3 圆相关的角度、线段的计算【例3】(2023·南阳二模)如图,AB,CD是☉O的两条直径①,点E是劣弧BD的中点②,连接AC,BE.若∠ACD=20°③,则∠ABE的度数为( D )
由邻补角的性质得进一步结论 ↓
4.(2023·濮阳模拟)如图,在 Rt△ABC中,∠A=90°,∠C=30°,AB=3,以点A为圆心,AB的长为半径画弧,分别交BC,AC于点E,D,则图中阴影部分的周长是 3+π .
类型3 圆相关的角度、线段的计算
5.(2023·商丘模拟)如图,四边形ABCD内接于☉O,且点D是优弧AB的中点,连接AC.若AB=AC,∠ACD=50°,则∠ABC的度数为( D )
6.(2023·仁怀模拟)如图,四边形ABCD的对角线AC是☉O的直径,AB=AD,∠AOD=110°,则∠BCD= 110 °.
相关课件
这是一份中考数学考点选填题针对训练真题函数图象-中考数学第三轮专题复习课件,共14页。PPT课件主要包含了由题中条件得基本结论等内容,欢迎下载使用。
这是一份数学中考考点针对训练历年真题半角模型课件,共25页。PPT课件主要包含了CONTENTS,模型解读,模型归纳,模型应用,强化训练,原基本模型,方法一旋转法,由题中条件得基本结论,方法二翻折法,由勾股定理求解等内容,欢迎下载使用。
这是一份中考数学考点针对训练历年真题手拉手模型课件,共27页。PPT课件主要包含了CONTENTS,模型解读,模型归纳,模型应用,强化训练,AB∥CE,AC=CD+CE等内容,欢迎下载使用。









