2024-2025学年上海市杨浦区高三上册期中考试数学检测试题

这是一份2024-2025学年上海市杨浦区高三上册期中考试数学检测试题，共5页。试卷主要包含了填空题，选择题．，解答题．等内容，欢迎下载使用。
1. 不等式的解集是________．（结果用区间表示）
2. 已知全集，集合，；则________．（结果用区间表示）
3. 已知函数，则______，
4. 函数的最小正周期为_______.
5. 已知向量，，若，则__________.
6. 在二项式展开式中，前三项的系数依次成________数列．（填写“等差”或“等比”）
7. 已知函数的导数存在，的部分图像如图所示，设是由曲线与直线，及轴围成的平面图形的面积，则在区间上，的最大值在________处取到.
8. 班级4名学生报名参加两项区学科竞赛，每人至少报一项，每项比赛参加的人数不限，则不同的报名结果有________种．（结果用具体数字表示）
9. 过抛物线的焦点，倾斜角为的直线交抛物线于（），则的值__________．
10. 为了提升全民身体素质，学校十分重视学生体育锻炼，某校篮球运动员进行投篮练习.如果他前一球投进则后一球投进的概率为；如果他前一球投不进则后一球投进的概率为.若他第2球投进的概率为，则他第1球投进的概率为__________.
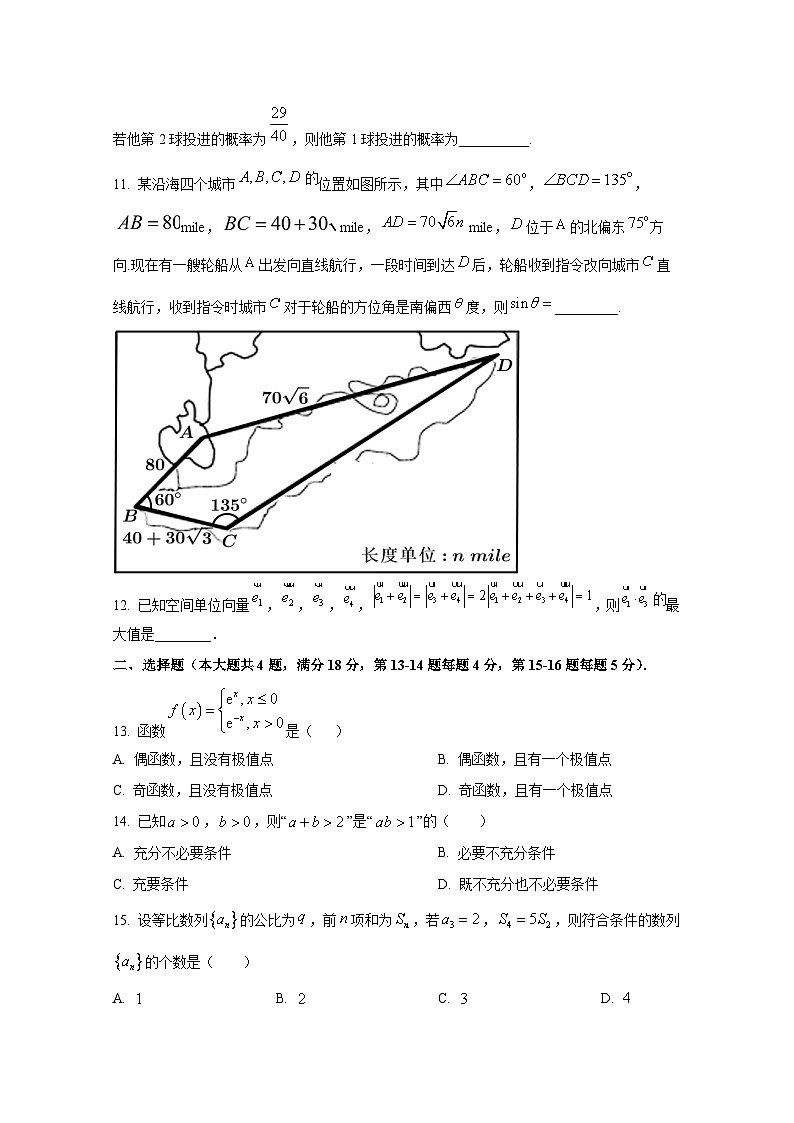
11. 某沿海四个城市位置如图所示，其中，，mile， mile， mile，位于的北偏东方向.现在有一艘轮船从出发向直线航行，一段时间到达后，轮船收到指令改向城市直线航行，收到指令时城市对于轮船的方位角是南偏西度，则_________.
12. 已知空间单位向量，，，，，则最大值是________．
二、选择题（本大题共4题，满分18分，第13-14题每题4分，第15-16题每题5分）．
13. 函数是（ ）
A. 偶函数，且没有极值点B. 偶函数，且有一个极值点
C. 奇函数，且没有极值点D. 奇函数，且有一个极值点
14. 已知，，则“”是“”的（ ）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
15. 设等比数列的公比为，前项和为，若，，则符合条件的数列的个数是（ ）
A. B. C. D.
16. 已知，则下列结论正确的个数是（ ）
①存在实数解；
②共有个不同的复数解；
③复数解的模长都等于；
④存在模长大于的复数解．
A. B. C. D.
三、解答题（满分78分，共有5题）．
17. 已知函数为奇函数．
（1）求的值并直接写出的单调性（无需说明理由）；
（2）若存在实数，使得成立，求实数的取值范围．
18. 如图所示，已知三棱台中，，，，，．
（1）求二面角余弦值；
（2）设E、F分别是棱、的中点，若平面，求棱台的体积．
19. 某市为提高市民对文明城市创建的认识，举办了“创建文明城市”知识竞赛，从所有答卷中随机抽取100份作为样本，将样本的成绩（满分100分，成绩均为不低于40分的整数）分成六段：，得到如图所示的频率分布直方图．
（1）求频率分布直方图中a的值；
（2）求样本成绩的；
（3）已知落在50,60的平均成绩是54，方差是7，落在60,70的平均成绩为66，方差是4，求两组成绩的总平均数和总方差．
20. 如图，在平面直角坐标系中，该点是椭圆上一点，从原点向圆作两条切线分别与椭圆交于点，，直线、斜率分别记为，.
（1）若圆与轴相切于椭圆的右焦点，求圆的方程；
（2）若，求证为定值并求出该定值；
（3）在（2）的情况下，求的最大值.
21. 已知，函数.
（1）当时，证明：；
（2）若恒成立，求a的取值范围；
（3）设集合，对于正整数m，集合，记中元素的个数为，求数列的通项公式.