

2024-2025学年上学期初中数学北师大版九年级期末必刷常考题之反比例函数的应用练习
展开
这是一份2024-2025学年上学期初中数学北师大版九年级期末必刷常考题之反比例函数的应用练习,共30页。
A.甲B.乙C.丙D.丁
2.(2024•闽清县模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,并结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36AB.最大电流是27A
C.最小电流是36AD.最小电流是27A
3.(2024秋•安平县期中)1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米的反比例函数,y与x之间有如下表的关系:
当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为( )
A.7米B.14米C.21米D.28米
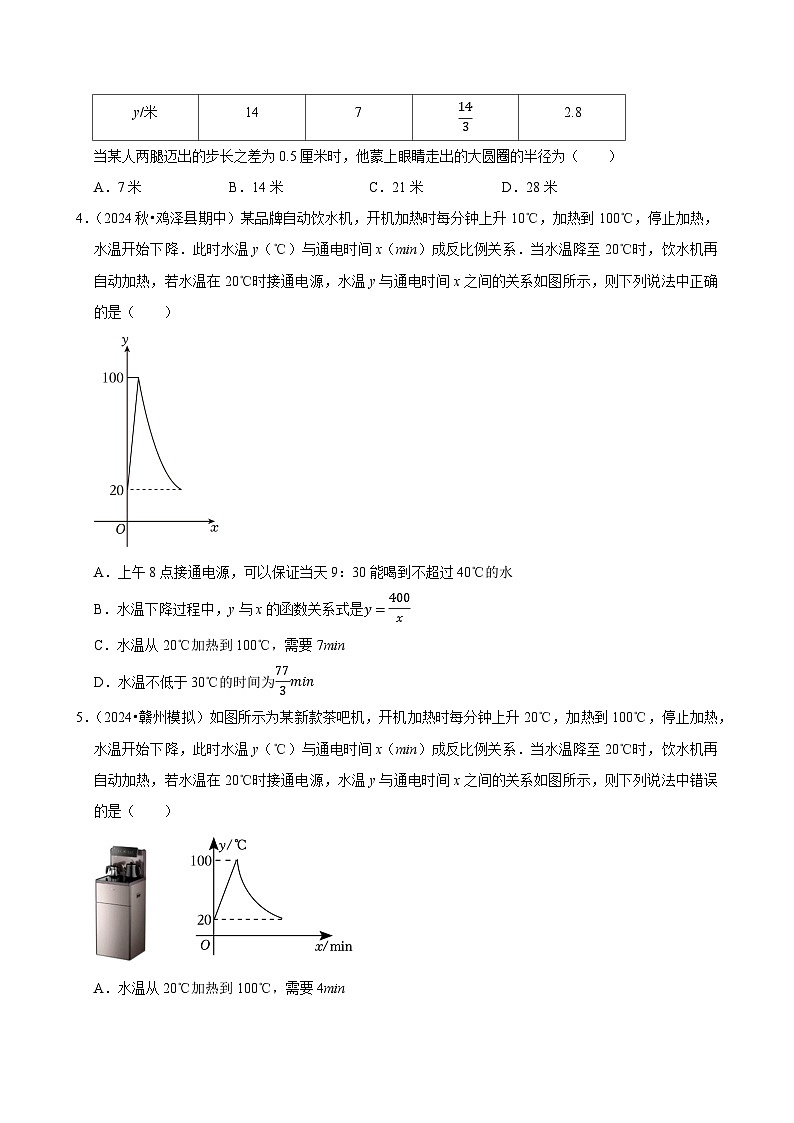
4.(2024秋•鸡泽县期中)某品牌自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温y(℃)与通电时间x(min)成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
A.上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水
B.水温下降过程中,y与x的函数关系式是y=400x
C.水温从20℃加热到100℃,需要7min
D.水温不低于30℃的时间为773min
5.(2024•赣州模拟)如图所示为某新款茶吧机,开机加热时每分钟上升20℃,加热到100℃,停止加热,水温开始下降,此时水温y(℃)与通电时间x(min)成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中错误的是( )
A.水温从20℃加热到100℃,需要4min
B.水温下降过程中,y与x的函数关系式是 y=400x
C.上午10点接通电源,可以保证当天10:30能喝到不低于38℃的水
D.在一个加热周期内水温不低于40℃的时间为7min
二.填空题(共5小题)
6.(2024•南通)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过10A,那么用电器可变电阻R应控制的范围是 .
7.(2024秋•泰山区期中)老李驾车从甲地到乙地,他以60千米/时的平均速度5小时到达目的地,当他按原路匀速返回甲地时,汽车的速度y(千米/时)与时间x(时)(x≠0)的函数关系式为 .
8.(2024•茌平区一模)验光师通过检测发现近视眼镜的度数y(度)与镜片焦距x(米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 度.
9.(2024•龙湖区一模)当温度不变时,某气球内的气压p(kPa)与气体体积V(m3)成反比例函数关系(其图象如图所示),已知当气球内的气压p>120kPa时,气球将爆炸,为了安全起见,气球内气体体积V满足的条件是 m3.
10.(2024春•曲沃县期末)收音机刻度盘上的频率f(kHz)是波长λ(m)的反比例函数,其函数图象如图所示,当λ=1000m时,该频道的频率为 kHz.
三.解答题(共5小题)
11.(2024秋•市中区期中)如图,在平面直角坐标系xOy中,点A(3,2)在反比例函数y=kx(k>0)的图象上,过点A作AC⊥x轴于点C.
(1)求反比例函数的表达式;
(2)如图,点B在反比例函数的图象上且在点A的右侧,过点B作BD⊥x轴于点D,连接AB、OB,OB交AC于点F,若点C是OD的中点,求△ABF的面积;
(3)点N在反比例函数的图象上,点M坐标为(0,m),若△CMN是等边三角形,求m的值.
12.(2024•两江新区校级模拟)如图1,E为矩形ABCD的边AD上的一个动点,F为射线DC上的一个动点,BE⊥AF于点G,AB=2,BC=4.设AE=x,CF=y1,y2=4x.
(1)请直接写出y1与x之间的函数关系式及对应的x的取值范围;
(2)在如图2所示的平面直角坐标系中画出y1,y2的图象,并写出函数y1的一条性质;
(3)结合你所画的函数图象,直接写出不等式y1≤y2的解集.
13.(2023秋•盘州市期末)如图,正比例函数y=−33x的图象与反比例函数y=kx(k≠0)的图象相交于点A(m,2)和点B.
(1)求反比例函数的表达式;
(2)若点C在y轴的正半轴上,且∠ACB=90°,求△ABC的面积;
(3)若点P(n,0)在x轴上,且∠APB为锐角,直接写出n的取值范围.
14.(2024秋•饶阳县期中)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气球体积V(m3)的反比例函数,其图象如图所示(千帕是一种压强单位).
(1)求出这个函数的解析式;
(2)当气球体积为0.8m3时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了完全起见,气球的体积应不小于 m3.
15.(2024秋•坪山区期中)【项目式学习】
项目主题:学科融合一一用数学的眼光观察世界.
项目背景:学习完相似三角形性质后,某学校科学小组的同学们尝试用数学的知识和方法来研究凸透镜成像规律.
项目素材:
素材一:透镜成像中,光路图的规律:通过透镜中心的光线不发生改变;平行于主光轴的光线经过折射后光线经过焦点.
素材二:设物距为u、像距为v和焦距为f,小明在研究的过程中发现了物距u、像距v和焦距f之间在成实像时存在着关系:1u+1v=1f.
【项目任务】根据项目素材解决问题:
任务一:小明先取物距u=1.5f,然后画出光路图(如图①),其中AB为物体,O为凸透镜MN的光心,入射光线AC∥光轴,折射光线CA'经过焦点C',A'B'为AB所成的像.
(1)根据光路图①可知,当u=1.5f时,ABA′B′= ;
(2)当u=2f时.请仿照图①的方法,在图②中画光路图;
任务二:凸透镜的焦距OE为6cm,蜡烛AB是4cm,离透镜中心O的距离是x cm(x>6)时,蜡烛的成像A′B′的高y cm,请你利用所学的知识求出y与x的关系式;
任务三:根据任务二的关系式得出表:
(1)m= ;
(2)当蜡烛的成像A′B′的高不小于2cm时,请在坐标系中画出它的图象;
2024-2025学年上学期初中数学北师大版九年级期末必刷常考题之反比例函数的应用
参考答案与试题解析
一.选择题(共5小题)
1.(2024•杭州四模)某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
A.甲B.乙C.丙D.丁
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】C
【分析】根据题意可知xy的值即为该级部的优秀人数,再根据图象即可确定丙学校的优秀人数最多,甲学校的优秀人数最少,乙、丁两学校的优秀人数相同.
【解答】解:根据题意,可知xy的值即为该校的优秀人数,
∵描述乙、丁两学校情况的点恰好在同一个反比例函数的图象上,
∴乙、丁两学校的优秀人数相同,
∵点丙在反比例函数图象上面,点甲在反比例函数图象下面,
∴丙学校的xy的值最大,即优秀人数最多,甲学校的xy的值最小,即优秀人数最少,
故选:C.
【点评】本题考查了反比例函数的应用,结合实际含义理解图象上点的坐标含义是解题的关键.
2.(2024•闽清县模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,并结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36AB.最大电流是27A
C.最小电流是36AD.最小电流是27A
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】A
【分析】可设I=UR,由于点(4,9)代入这个函数解析式,则可求得k的值,然后代入R=1求得I的值即可.
【解答】解:根据电压=电流×电阻,设I=UR,
将点(4,9)代入得9=U4,解得U=36,
∴I=36R;
若该电路的最小电阻值为1Ω,该电路能通过的最大电流是361=36(A),
故选:A.
【点评】本题考查了反比例函数的解析式,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
3.(2024秋•安平县期中)1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米的反比例函数,y与x之间有如下表的关系:
当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为( )
A.7米B.14米C.21米D.28米
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】D
【分析】先用待定系数法求出反比例函数解析式,再把x=0.5代入反比例函数的解析式求解即可.
【解答】解:设y与x之间的函数表达式为y=kx,
∴7=k2,
∴k=14,
∴y与x之间的函数表达式为y=14x;
当x=0.5时,y=140.5=28(米),
∴当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为28米,
答:当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为28米;
故选:D.
【点评】本题考查了反比例函数的应用,正确的理解题意是解题的关键.
4.(2024秋•鸡泽县期中)某品牌自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温y(℃)与通电时间x(min)成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
A.上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水
B.水温下降过程中,y与x的函数关系式是y=400x
C.水温从20℃加热到100℃,需要7min
D.水温不低于30℃的时间为773min
【考点】反比例函数的应用.
【专题】推理能力.
【答案】D
【分析】该题为反比例函数与一次函数的实际应用的典型题目——浓度、温度问题,先利用待定系数法求函数的解析式,再利用解析式求得对应信息.
【解答】解:A、根据题意可得y与x的函数关系式是y=800x,令y=20,则800x=20,
∴x=40,即饮水机每经过40min,要重新从开始加热一次从8点至9:30,经过的时间为90min,90﹣40×2=10min,而水温加热到100℃,需要的时间为100−2010=8min,故9:30时,饮水机第三次从开始加热了10min,令x=10,则y=800x=80010=80,即9:30时,饮水机的水温为80℃,故A选项不符合题意;
B、由题意可得点(8,100)在反比例函数的图象上,设反比例函数的解析式为y=kx,将点(8,100)代入,可得k=800,
∴水温下降过程中,y与x的函数关系式是y=800x,故B选项不符合题意;
C、∵开机加热时水温每分钟上升10℃,
∴水温从20℃升高到100℃,需要的时间为100−2010=8min,故C选项不符合题意;
D、水温从20℃加热到100℃所需要的时间为30−2010=1min,
令y=30,则800x=30,解得x=803,
∴水温不低于30℃的时间为803−1=773min,故D选项符合题意.
故选:D.
【点评】本题考查了一次函数和反比例函数的应用,数形结合是解决本题的关键.
5.(2024•赣州模拟)如图所示为某新款茶吧机,开机加热时每分钟上升20℃,加热到100℃,停止加热,水温开始下降,此时水温y(℃)与通电时间x(min)成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中错误的是( )
A.水温从20℃加热到100℃,需要4min
B.水温下降过程中,y与x的函数关系式是 y=400x
C.上午10点接通电源,可以保证当天10:30能喝到不低于38℃的水
D.在一个加热周期内水温不低于40℃的时间为7min
【考点】反比例函数的应用.
【专题】一次函数及其应用;反比例函数及其应用;运算能力;应用意识.
【答案】D
【分析】根据水温升高的速度,即可求出水温从20℃加热到100℃所需的时间;设水温下降过程中,y与x的函数关系式为y=kx,根据待定系数法即可求解;先求出当水温下降到20摄氏度所需时间为20min,即一个循环为20min,30﹣20=10,将x=10代入反比例函数解析式中求出此时水温即可判断;分别求出在加热过程和降温过程中水温为40摄氏度时的时间,再相减即可判断.
【解答】解:∵开机加热时每分钟上升20℃,
∴水温从20℃加热到100℃,所需时间为100−2020=4(min),故A选项正确,不符合题意;
设水温下降过程中,y与x的函数关系式为y=kx,
由题意得,点(4,100)在反比例函数y=kx的图象上,
∴4=k100,
解得:k=400,
∴水温下降过程中,y与x的函数关系式是y=400x,故B选项正确,不符合题意;
令y=20,则400x=20,
∴x=20,
∴从开机加热到水温降至20℃需要20min,即一个循环为20min,
水温y(℃)与通电时间x(min)的函数关系式为y=20x+20(0≤x≤4)y=400x(4<x≤20),
上午10点到10:30共30分钟,30﹣20=10,
∴当x=10时,y=40010=40,
即此时的水温为40℃>38℃,故C选项正确,不符合题意;
在加热过程中,水温为40℃时,20x+20=40,
解得:x=1,
在降温过程中,水温为40℃时,40=400x,
解得:x=10,
∵10﹣1=9,
∴一个加热周期内水温不低于40℃的时间为9min,故D选项错误,符合题意.
故选:D.
【点评】本题主要考查反比例函数和一次函数的应用、用待定系数法求反比例函数解析数,解题关键在于读懂图象,灵活运用所学知识解决问题.
二.填空题(共5小题)
6.(2024•南通)已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过10A,那么用电器可变电阻R应控制的范围是 R≥3.6Ω .
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】见试题解答内容
【分析】根据图象中的点的坐标先求反比例函数关系式,再由电流不能超过10A列不等式,求出结论,并结合图象.
【解答】解:设反比例函数关系式为:I=kR,
把(9,4)代入得:k=4×9=36,
∴反比例函数关系式为:I=36R,
当I≤10时,则36R≤10,
R≥3.6,
故答案为:R≥3.6Ω.
【点评】本题是反比例函数的应用,会利用待定系数法求反比例函数的关系式,并正确认识图象,运用数形结合的思想,与不等式或等式相结合,解决实际问题.
7.(2024秋•泰山区期中)老李驾车从甲地到乙地,他以60千米/时的平均速度5小时到达目的地,当他按原路匀速返回甲地时,汽车的速度y(千米/时)与时间x(时)(x≠0)的函数关系式为 y=300x(x>0) .
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】y=300x(x>0)
【分析】根据速度×时间=路程,可以求出甲地到乙地的路程;再根据行驶速度=路程÷时间,得到y与x的函数解析式.
【解答】解:由已知得:甲地到乙地的路程=60×5=300(千米),
则汽车的速度y(千米/时)与时间x(时)(x≠0)的函数关系式为y=300x(x>0).
故答案为:y=300x(x>0).
【点评】本题考查反比例函数的应用,关键是列出函数解析式.
8.(2024•茌平区一模)验光师通过检测发现近视眼镜的度数y(度)与镜片焦距x(米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 200 度.
【考点】反比例函数的应用.
【专题】函数思想;模型思想;应用意识.
【答案】200.
【分析】由已知设y=kx,则有图象知点(0.2,500)满足解析式,代入求k=100,则解析式为:y=100x,令x=0.25,x=0.5时,分别求y的值后作差即可.
【解答】解:设y=kx(k≠0),
∵(0.2,500)在图象上,
∴k=500×0.2=100,
∴函数解析式为:y=100x,
当x=0.25时,y=1000.25=400,
当x=0.5时,y=1000.5=200,
∴度数减少了400﹣200=200(度),
故答案为:200.
【点评】本题考查待定系数法求反比例函数解析式,以及反比例函数的实际应用,读懂题意,掌握课本知识是解决问题的关键.
9.(2024•龙湖区一模)当温度不变时,某气球内的气压p(kPa)与气体体积V(m3)成反比例函数关系(其图象如图所示),已知当气球内的气压p>120kPa时,气球将爆炸,为了安全起见,气球内气体体积V满足的条件是 35 m3.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】35.
【分析】根据题意可知温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,且过点(1.2,60)故p•V=72;故当p≤120,可判断V应满足的条件.
【解答】解:设球内气体的气压p(kPa)和气体体积V(m3)的关系式为p=kV,
∵图象过点(1.6,60),
∴60=k1.2,
∴k=72,
由已知得p=72V图象在第一象限内,
∴p随V的增大而减小,
∴当p≤120时,V≥72120,
∴V≥35,即不小于35m3,
故答案为:35.
【点评】本题考查反比例函数的应用,解题的关键是根据图象上的已知点的坐标,利用待定系数法求出函数解析式.
10.(2024春•曲沃县期末)收音机刻度盘上的频率f(kHz)是波长λ(m)的反比例函数,其函数图象如图所示,当λ=1000m时,该频道的频率为 300 kHz.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;推理能力.
【答案】300.
【分析】用待定系数法求出函数表达式,进而求解.
【解答】解:设函数的表达式为:f=kλ,
将点(200,1500)代入上式得:1500=k200,
解得:k=300000,
则函数的表达式为:y=300000λ,
当λ=1000时,y=300000λ=300,
故答案为:300.
【点评】本题考查的是反比例函数的应用,求出函数表达式是解题的关键.
三.解答题(共5小题)
11.(2024秋•市中区期中)如图,在平面直角坐标系xOy中,点A(3,2)在反比例函数y=kx(k>0)的图象上,过点A作AC⊥x轴于点C.
(1)求反比例函数的表达式;
(2)如图,点B在反比例函数的图象上且在点A的右侧,过点B作BD⊥x轴于点D,连接AB、OB,OB交AC于点F,若点C是OD的中点,求△ABF的面积;
(3)点N在反比例函数的图象上,点M坐标为(0,m),若△CMN是等边三角形,求m的值.
【考点】反比例函数综合题.
【专题】代数几何综合题;运算能力;推理能力.
【答案】(1)反比例函数的表达式为y=23x;
(2)334;
(3)m的值为1或﹣5.
【分析】(1)将点A(3,2)代入反比例函数y=kx(k>0),于是得到结论;
(2)由AC⊥x轴,得到OC=3,根据点C是OD的中点,得到CD=3,得到点B和点D横坐标相等,将x=23代入y=23x得到y=1,求得点B坐标为(23,1),解方程得到OB的解析式,得到点F坐标,根据三角形的面积公式即可得到结论;
(3)①当M在y轴正半轴时,如图1,在OM延长线上取点G,使得∠MGN=60°,在MO延长线上取点H使得∠MHC=60°,过点N作Nl⊥y轴于点1,得到∠NMC=60°,MN=HC,在Rt△OHC中,∠OHC=60°,得到∠OCH=30°,求得OH=12CH,设OH=a,则HC=2a,根据勾股定理得到a=±1(负值舍去),求得OH=1,MH=m+1,HC=2,根据全等三角形的性质得到GM=HC=2,GN=MH=m+1,求得GO=m+2,得到点B坐标,解方程得到m=1;②当M在y轴负半轴时,如图2在CO延长线上取点P,使得∠NPC=60°,在OC延长线上取点Q,使得∠MOC=60°,过点N作NR⊥x轴于点R,根据等边三角形的性质得到∠NCM=60°,CN=CM,求得OQ=12MQ,根据勾股定理得到b=±33m(负值舍去),根据直角三角形的性质即可得到结论.
【解答】解:(1)将点A(3,2)代入y=kx得2=k3,
解得k=23,
∴反比例函数的表达式为y=23x;
(2)∵AC⊥x轴,
∴OC=3,
∵点C是OD的中点,
∴CD=3,
∵BD⊥x轴于点D,
∴点B和点D横坐标相等,
将x=23代入y=23x得y=1,
∴点B坐标为(23,1),
设OB的解析式为y=kx,
将B(23,1)代入得1=23k,
解得k=123,
∴OB的解析式为y=123x,
将x=3代入,得y=12,
∴点F坐标为(3,12),
∴AF=2−12=32,
∴S△ABF=12AF•CD=12×32×3=334;
(3)①当M在y轴正半轴时,如图1,
在OM延长线上取点G,使得∠MGN=60°,在MO延长线上取点H使得∠MHC=60°,
过点N作NI⊥y轴于点I,
∵△CMN为等边三角形,
∴∠NMC=60°,MN=HC,
在Rt△OHC中,∠OHC=60°,
∴∠OCH=30°,
∴OH=12HC,
设OH=a,则 HC=2a,由勾股定理得
OH2+OC2=HC2,
即a2+(3)2=(2a)2,
解得a=±1(负值舍去),
∴OH=1,MH=m+1,HC=2,
∵∠MGN=∠MHC=∠NMC=60°,
∴∠GNM+∠GMN=∠GMN+∠HMC=120°,
∴∠GNM=∠HMC,
∴△MNG≌△CMH(ASA),
∴GM=HC=2,GN=MH=m+1,
∴GO=m+2,
在Rt△GNI中,∠NGM=60°,
∴∠GNI=30°,
∴IG=12GN=m+12,IO=GO﹣GI=m+32,
∴IN=3GI=32(m+1),
∴点B坐标为(32m+32,m+32 ),
∵N为反比例上的点,
∴(32m+32)×m+32 =23,
即(m+1)(m+3)=8,
∵m为整数且在y轴正半轴上,
∴m=1;
②当M在y轴负半轴时,如图2
在CO延长线上取点P,使得∠NPC=60°,在OC延长线上取点Q,使得∠MOC=60°,
过点N作NR⊥x轴于点R,
∵△CMN为等边三角形,
∴∠NCM=60°,CN=CM,
在Rt△MOQ中,∠OQM=60°,
∴∠OMQ=30°,
∴OQ=12MQ,
设OQ=b,则QM=2b,由勾股定理得OQ2+OM2=MQ2,
即b2+(﹣m)2=(2b)2,
解得b=±33m(负值舍去),
∴OQ=−33m,QM=−233m,CQ=−33(m+3),
同理可证:△MCQ≌△CNP,
PC=QM=−233m,PN=CQ=−33(m+3),
在Rt△NPR中,∠NPR=60°,
∴∠PNR=30°,
∴PR=12PN=−36(m+3),
∴RN=3PR=−12(m+3),
∴RO=−233m−3−[−36(m+3)]=−32(m+1),
∴N点坐标为[32(m+1),12(m+3)],
∵N为反比例上的点,
∴32(m+1)×12(m+3)=23,
即(m+1)(m+3)=8,
∵m为整数且在y轴负半轴上
∴m=﹣5
∴综上所述,m的值为1或﹣5.
【点评】本题是反比例函数的综合题,考查了待定系数法求函数的解析式,三角形的面积的计算,全等三角形的判定和性质,勾股定理,等边三角形的性质,正确地作出辅助线是解题的关键.
12.(2024•两江新区校级模拟)如图1,E为矩形ABCD的边AD上的一个动点,F为射线DC上的一个动点,BE⊥AF于点G,AB=2,BC=4.设AE=x,CF=y1,y2=4x.
(1)请直接写出y1与x之间的函数关系式及对应的x的取值范围;
(2)在如图2所示的平面直角坐标系中画出y1,y2的图象,并写出函数y1的一条性质;
(3)结合你所画的函数图象,直接写出不等式y1≤y2的解集.
【考点】反比例函数综合题.
【专题】代数几何综合题;解直角三角形及其应用;数据分析观念.
【答案】(1)y1=−2x+2(0≤x≤1)2x−2(1<x≤4);
(2)函数图象见解答;当0≤x≤1时,y1随x的增大而减小,当x>1时,y1随x的增大而增大(答案不唯一);(3)0<x≤2.
【分析】(1)当点F在线段CD上时,证明∠EAG=∠ABE,则tan∠EAG=tan∠ABE,即可求解;当点F在点C下方时,同理可解;
(2)通过对上述点描点、连线绘制图象,进而求解;
(3)观察函数图象即可求解.
【解答】解:(1)当点F在线段CD上时,如图1,
由题意得:AE=x,AD=4,AB=2,DF=4﹣y1,
∵BE⊥AF,即∠AGB=90°,
∴∠EAG+∠AEG=90°,
∵∠AEG+∠ABE=90°,
∴∠EAG=∠ABE,
∴tan∠EAG=tan∠ABE,
∴AEAB=DFAD,即x2=4−y14,
解得:y1=﹣2x+2(0≤x≤1),
当点F在点C下方时,
同理可得:tan∠EAG=tan∠ABE,
∴AEAB=DFAD,即2+y14=x2,
y1=2x﹣2(x>1),
E在AD上运动,AE=x,AD=BC=4,
当y=2x﹣2时,x的取值范围应该是1<x≤4,
则y1=−2x+2(0≤x≤1)2x−2(1<x≤4);
(2)对于y1,当x=0时,y1=2,当x=1时,y1=0,当x=2时,y1=2,
对于y2,当x=1时,y2=4,当x=2时,y2=2,当x=4时,y2=1,
通过对上述点描点、连线绘制图象如下:
从y1的图象看,当0≤x≤1时,y1随x的增大而减小,当x>1时,y1随x的增大而增大(答案不唯一);
(3)从函数图象看,不等式y1≤y2的解集为:0<x≤2.
【点评】本题为反比例函数综合运用,涉及到函数作图、一次函数和反比例函数的基本性质、解直角三角形等,有一定能够的综合性,难度适中.
13.(2023秋•盘州市期末)如图,正比例函数y=−33x的图象与反比例函数y=kx(k≠0)的图象相交于点A(m,2)和点B.
(1)求反比例函数的表达式;
(2)若点C在y轴的正半轴上,且∠ACB=90°,求△ABC的面积;
(3)若点P(n,0)在x轴上,且∠APB为锐角,直接写出n的取值范围.
【考点】反比例函数综合题.
【专题】代数几何综合题;运算能力;推理能力.
【答案】(1)反比例函数的表达式为y=−43x;
(2)△ABC的面积为83.;
(3)n的取值范围是:n<﹣4或n>4.
【分析】(1)将点A(m,2)代入y=−33x,可求出点A坐标,代入y=kx,求出k值,即可求解;
(2)根据反比例函数的对称性,可得点B坐标,由直角三角形斜边中线等于斜边的一半,可求OC的长度,进而求出S△AOC+S△BOC,即可求解;
(3)找到∠APB为直角时的临界点,分两种情况讨论,即可求解.
【解答】解:(1)将A(m,2)代入y=−33x得−33m=2,
∴m=﹣23,
∴A(﹣23,2),
将点A(﹣23,2)代入y=kx得k=﹣43,
∴y=−43x.
故答案为:反比例函数的表达式为y=−43x;
(2)依题意可得:点A和点B关于原点对称,则有点O是AB的中点,
∴点B(23,﹣2),
∵∠ACB=90°,
∴CO=AO=BO=12AB,
∵AO=(−23)2+22=4,
∴CO=4,
则点C(0,4),
∴S△ABC=S△AOC+S△BOC=12×4×23+12×4×23=83.
故答案为:△ABC的面积为83;
(3)由(2)知:AB=8,
①当点P在x轴负半轴上时,当OP1=4时,∠AP1B=90°,
∴当∠AP1B为锐角时,OP1>4,即:n<﹣4,
②当点P在x轴正半轴上时,当OP2=4时,∠AP2B=90°,
∴当∠AP2B为锐角时,OP2>4,即:n>4,
故答案为:n的取值范围是:n<﹣4或n>4.
【点评】本题是反比例函数的综合题,考查了反比例函数与一次函数交点,求反比例函数解析式,反比例函数的对称性,直角三角形斜边中线等于斜边一半,解题的关键是:熟练掌握直角三角形斜边中线等于斜边一半,及其逆应用.
14.(2024秋•饶阳县期中)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气球体积V(m3)的反比例函数,其图象如图所示(千帕是一种压强单位).
(1)求出这个函数的解析式;
(2)当气球体积为0.8m3时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了完全起见,气球的体积应不小于 23 m3.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】(1)函数的解析式为P=96V;
(2)气球内的气压是120千帕;
(3)23.
【分析】(1)直接运用待定系数法即可解答;
(2)将V=0.8代入(1)中的函数式求p即可;
(3)将p=144代入(1)中的函数式求V即可解答.
【解答】解:(1)设这个函数的解析式p=kV,
由函数图象可知,k=1.6×60=96,
∴这个函数的解析式为p=96V;
(2)当V=0.8时,p=960.8=120(千帕),
答:气球内的气压是120千帕;
(3)根据题意,当p≤144时,为安全范围,
∴96V≤144,
解得,V≥23,
故为了安全起见,气球的体积应不小于23m3.
故答案为:23.
【点评】本题主要考查了反比例函数的实际应用,正确建立函数关系式并会运用函数关系式是解题的关键.
15.(2024秋•坪山区期中)【项目式学习】
项目主题:学科融合一一用数学的眼光观察世界.
项目背景:学习完相似三角形性质后,某学校科学小组的同学们尝试用数学的知识和方法来研究凸透镜成像规律.
项目素材:
素材一:透镜成像中,光路图的规律:通过透镜中心的光线不发生改变;平行于主光轴的光线经过折射后光线经过焦点.
素材二:设物距为u、像距为v和焦距为f,小明在研究的过程中发现了物距u、像距v和焦距f之间在成实像时存在着关系:1u+1v=1f.
【项目任务】根据项目素材解决问题:
任务一:小明先取物距u=1.5f,然后画出光路图(如图①),其中AB为物体,O为凸透镜MN的光心,入射光线AC∥光轴,折射光线CA'经过焦点C',A'B'为AB所成的像.
(1)根据光路图①可知,当u=1.5f时,ABA′B′= 12 ;
(2)当u=2f时.请仿照图①的方法,在图②中画光路图;
任务二:凸透镜的焦距OE为6cm,蜡烛AB是4cm,离透镜中心O的距离是x cm(x>6)时,蜡烛的成像A′B′的高y cm,请你利用所学的知识求出y与x的关系式;
任务三:根据任务二的关系式得出表:
(1)m= 3 ;
(2)当蜡烛的成像A′B′的高不小于2cm时,请在坐标系中画出它的图象;
【考点】反比例函数综合题.
【专题】反比例函数及其应用;应用意识.
【答案】任务一:(1)12;(2)光路图见解答.
任务二:y=24x−6.
任务三:(1)3;(2)图象见解答.
【分析】任务一:(1)根据素材知识1u+1v=1f,把u=1.5f代入求出v=3f,然后由平行线分线段成比例得到ABA′B′=uv,即可得出答案;
(2)仿照光路图①从点A画出两条光路的交点确定AB的成像A′B′的大小及位置.
任务二:根据1u+1v=1f和ABA′B′=uv,代入相关数据即可求出y与x的表达式.
任务三:(1)把x=14,y=m代入y=24x−6求解即可得出m的值;
(2)先通过平移反比例函数y=24x的图象即可得出y=24x−6的图象,然后由y=24x−6≥2和x>6得出x的范围,最后根据x的范围画出图象即可.
【解答】任务一:
(1)根据素材二可知1u+1v=1f,把u=1.5f代入得:
11.5f+1v=1f.
∴v=3f.
∵AB∥A′B′,
∴ABA′B′=BOB′O=uv=1.5f3f=12.
故答案为:12.
(2)过点A作光轴的平行线交透镜MN于点C,连接CC′、AO并延长交于点A′,过点A′作A′B′垂直光轴于点B′,A′B′为蜡烛AB经过透镜MN所成的像,如图所示:
任务二:
由素材二可知1u+1v=1f,把u=x,f=6代入,则v=6xx−6.
由任务一可知ABA′B′=uv,把u=4,v=y代入,即4y=uv.
∴4y=x−66.
整理得y=24x−6.
故y与x的关系式为y=24x−6.
任务三:
(1)把x=14,y=m代入y=24x−6,m=3.
故答案为:3.
(2)根据函数图象平移性质,函数y=24x−6的图象相当于函数y=24x的图象向右平移6个单位.
当y=24x−6≥2时,x≤18,根据任务二要求x>6,所以6<x≤18.
因此其图象如下:
【点评】本题考查了反比例函数的图象及应用,平行线分线段成比例的性质.根据平行线分线段成比例线段结合素材知识求出函数表达式是解答本题的关键.
考点卡片
1.反比例函数的应用
(1)利用反比例函数解决实际问题
①能把实际的问题转化为数学问题,建立反比例函数的数学模型.②注意在自变量和函数值的取值上的实际意义.③问题中出现的不等关系转化成相等的关系来解,然后在作答中说明.
(2)跨学科的反比例函数应用题
要熟练掌握物理或化学学科中的一些具有反比例函数关系的公式.同时体会数学中的转化思想.
(3)反比例函数中的图表信息题
正确的认识图象,找到关键的点,运用好数形结合的思想.
2.反比例函数综合题
(1)应用类综合题
能够从实际的问题中抽象出反比例函数这一数学模型,是解决实际问题的关键一步,培养了学生的建模能力和从实际问题向数学问题转化的能力.在解决这些问题的时候我们还用到了反比例函数的图象和性质、待定系数法和其他学科中的知识.
(2)数形结合类综合题
利用图象解决问题,从图上获取有用的信息,是解题的关键所在.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法x/厘米
1
2
3
5
y/米
14
7
143
2.8
物距x/cm
…
8
10
12
14
16
…
像高y/cm
…
12
6
4
m
2.4
…
x/厘米
1
2
3
5
y/米
14
7
143
2.8
物距x/cm
…
8
10
12
14
16
…
像高y/cm
…
12
6
4
m
2.4
…
相关试卷
这是一份2024-2025学年上学期初中数学北师大版九年级期末必刷常考题之视图练习,共17页。试卷主要包含了cm等内容,欢迎下载使用。
这是一份2024-2025学年上学期初中数学北师大版九年级期末必刷常考题之投影练习,共20页。
这是一份2024-2025学年上学期初中数学北师大版九年级期末必刷常考题之成比例线段练习,共11页。









