山东省德州市临邑县2023-2024学年八年级上学期期末考试数学试卷(含解析)

这是一份山东省德州市临邑县2023-2024学年八年级上学期期末考试数学试卷(含解析)，共22页。试卷主要包含了考生必须保持答题卡的整洁，阅读以下作图步骤等内容，欢迎下载使用。
八年级数学试题
（满分150分 时间120分钟）
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置．
2．请将选择题答案用2B铅笔填涂在答题卡指定题号里；将非选择题的答案用0.5毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内，答在试题卷上无效．
3．考生必须保持答题卡的整洁．
一、选择题（共12小题，每小题4分，共48分）
1．杭州第19届亚运会于2023年9月23日—2023年10月8日举行，在整个赛事中，中国健儿表现出了不畏艰难、团结向上的精神，最终以201金位列第一的成绩完美收官．以下体育运动图标是轴对称图形的是（ ）
A．B．
C．D．
2．下列二次根式中，与属于同类二次根式的是（ ）
A．B．C．D．
3．下列乘法算式中，正确的是（ ）
A．B．
C．D．
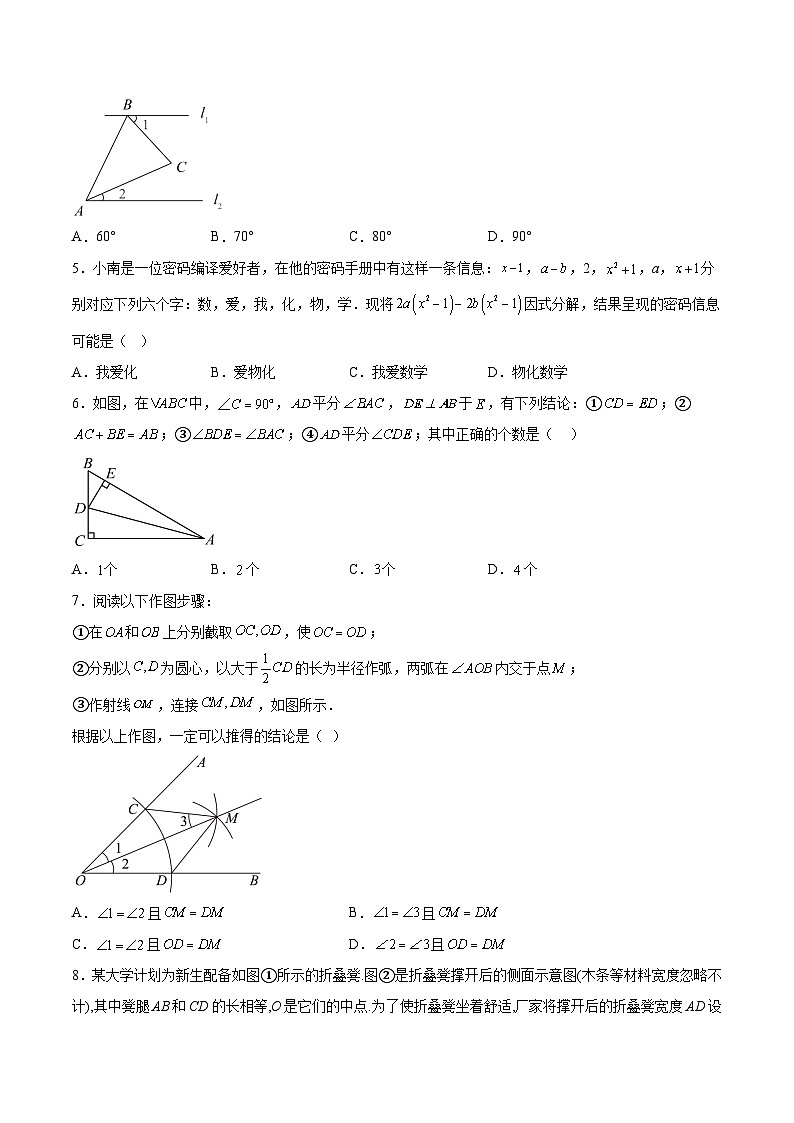
4．如图，直线，AB＝AC，∠BAC＝40°，则∠1＋∠2的度数是（ ）
A．60°B．70°C．80°D．90°
5．小南是一位密码编译爱好者，在他的密码手册中有这样一条信息：，，2，，a，分别对应下列六个字：数，爱，我，化，物，学．现将因式分解，结果呈现的密码信息可能是（ ）
A．我爱化B．爱物化C．我爱数学D．物化数学
6．如图，在中，，平分，于，有下列结论：①；②；③；④平分；其中正确的个数是（ ）
A．个B．个C．个D．个
7．阅读以下作图步骤：
①在和上分别截取，使；
②分别以为圆心，以大于的长为半径作弧，两弧在内交于点；
③作射线，连接，如图所示．
根据以上作图，一定可以推得的结论是（ ）

A．且B．且
C．且D．且
8．某大学计划为新生配备如图①所示的折叠凳.图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,则由以上信息可推得CB的长度也为30 cm,依据是( )
A．SASB．ASAC．SSSD．AAS
9．如图，中，是角平分线，垂足为，垂足为，与交于，下列说法不一定正确的是（ ）
A．也是中线B．平分
C．D．
10．四元玉鉴是我国古代数学重要著作之一，为元代数学家朱世杰所著．该著作记载了“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽”大意是：现请人代买一批椽，这批椽的价钱为6210文．如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？（椽，装于屋顶以支持屋顶盖材料的木杆）设这批椽有x株，则符合题意的方程是（ ）
A．B．C．D．
11．若关于x的一元一次不等式组的解集为x≥5，且关于y的分式方程有非负整数解，则符合条件的所有整数a的和为（ ）
A．-1B．-2C．-3D．0
12．如图，在中，和的平分线相交于点O，交干E，交于F，过点O作于D，下列三个结论：①∠；②当时，；③若，则．其中正确的是（ ）
A．①②B．②③C．①②③D．①③
二、填空题（本题共计6小题，每题4分，共计24分）
13．若代数式有意义，则x的取值范围 ．
14．已知，，则的值是 ．
15．如图，B处在A处的南偏西方向，C处在A处的南偏东方向，C处在B处的北偏东方向，求∠ACB的度数
16．已知关于x的分式方程的增根是，则m的值为 ．
17．如图所示，在边长为2的正三角形ABC中，E、F、G分别为AB、AC、BC的中点，点P为线段EF上一个动点，连接BP、GP，则的周长的最小值是 ．
18．如图，∠AOB=120°，点P为∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：①PM=PN；②OM+ON=OP；③四边形PMON的面积保持不变；④△PMN的周长保持不变．其中说法正确的是 ．(填序号)
三、解答题（本题共计7小题，共计78分）
19．（1）因式分解：；
（2）计算：．
20．（1）先化简，再求值：，其中，．
（2）解分式方程：．
21．如图所示，平分，，，垂足分别为B，D．若，，求四边形的面积．
22．如图，在平面直角坐标系中，点O为坐标原点，已知三个定点坐标分别为，，．
(1)画出关于x轴对称后的图形，并写出各点的坐标．
______，______，______．
(2)画出点C关于直线对称的点以及求出的坐标，连接，，，并求出的面积．
23．2024年龙年春晚吉祥物形象“龙辰辰”正式发布亮相，作为中华民族重要的精神象征和文化符号，千百年来，龙的形象贯穿文学、艺术、民俗、服饰、绘画等各个领域，也呈现了吉祥如意、平安幸福的美好寓意．吉祥物“龙辰辰”的产生受到众人的热捧．某工厂计划加急生产一批该吉祥物，决定选择使用A、B两种材料生产吉祥物．已知使用B材料的吉祥物比A材料每个贵50元，用3000元购买用A材料生产吉祥物的数量是用1500元购买B材料生产吉祥物数量的4倍．
(1)求售卖一个A材料、一个B材料的吉祥物各需多少元？
(2)一所中学为了激励学生奋发向上，准备用不超过3000元购买A、B两种材料的吉祥物共50个，来奖励学生．恰逢工厂对两种材料吉祥物的价格进行了调整：使用A材料的吉祥物的价格按售价的九折出售，使用B材料的吉祥物比售价提高了，那么该学校此次最多可购买多少个用B材料的吉祥物？
24．定义：若分式P与分式Q的差等于它们的积，即，则称分式P与分式Q互为“关联分式”．如与，因为，所以与互为“关联分式”，其中一个分式是另外一个分式的“关联分式”．
(1)请通过计算判断分式是不是分式的“关联分式”．
(2)求分式的“关联分式”．
25．在等边中，线段为边上的中线．动点D在直线上时，以为一边在的下方作等边，连接．
(1)若点D在线段上时（如图1），则 （填“＞”、“＜”或“＝”）， 度；
(2)设直线与直线的交点为O．
①当动点D在线段的延长线上时（如图2），试判断与的数量关系，并说明理由；
②当动点D在直线上时，试判断是否为定值？若是，请直接写出的度数．
答案与解析
1．A
解：A选项：沿一条直线折叠，直线两旁的部分能够互相重合，故是轴对称图形，符合题意；
B选项：沿一条直线折叠，直线两旁的部分不能够互相重合，故不是轴对称图形，不符合题意；
C选项：沿一条直线折叠，直线两旁的部分不能够互相重合，故不是轴对称图形，不符合题意；
D选项：沿一条直线折叠，直线两旁的部分不能够互相重合，故不是轴对称图形，不符合题意．
故选：A．
2．C
解：，，
则与是同类二次根式，
故选：C．
3．D
解：A、，故原计算错误，不合题意；
B、，故原计算错误，不合题意；
C、，故原计算错误，不合题意；
D、，故原计算正确，符合题意；
故选：D．
4．B
解：∵AB＝AC，∠BAC＝40°，
∴∠ABC=（180°-∠BAC）＝（180°-40°）=70°，
∵
∴
∴
故选：B．
5．C
解：∵
，
分别对应4个汉字：我，爱，数，学．
则呈现的密码信息可能是：我爱数学．
故选：C．
6．D
解：∵平分，
∴，
∵，
∴，
又∵，
∴，
∴，，，故①正确；
∴平分，，②④正确；
∵
∴
∴，③正确；
故选：D
7．A
解：由作图过程可得：，
∵，
∴．
∴．
∴A选项符合题意；
不能确定,则不一定成立，故B选项不符合题意；
不能确定,故C选项不符合题意，
不一定成立，则不一定成立，故D选项不符合题意．
故选A．
8．A
解：∵O是AB、CD的中点，
∴OA=OB，OC=OD，
在△AOD和△BOC中，
，
∴△AOD≌△BOC（SAS），
∴CB=AD，
∵AD=30cm，
∴CB=30cm．
故选A
9．A
解：A．等腰三角形底边上的中线，顶角平分线，底边上的高线才三线合一，而不是等腰三角形，因此不一定是中线，故A符合题意；
B．∵是角平分线，，，
∴，
∵，
∴，
∴，
∴平分，故B不符合题意；
CD．∵，
∴，
∵，
∴垂直平分，
∴，，故CD不符合题意．
故选：A．
10．D
解：∵这批椽有株，少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，
∴一株椽的价格为文，
根据题意得：．
故选：D．
11．B
解析：由题意，得
，即
，即
∴，即
，解得
有非负整数解，即
∴a≥-2且a≠2
∴且
∴符合条件的所有整数a的数有：-2，-1,0,1
又∵为非负整数解，
∴符合条件的所有整数a的数有：-2,0
∴其和为
故选：B.
12．C
解：∵和的平分线，相交于点O，
∴，，
∴
=
=
=，故①正确；
∵，
∴，
∵，分别是和的平分线，
∴，
∴，
∴，
∴，
如图所示，在上取一点H，使，

∵是的角平分线，
∴，
在和中，
，
∴，
∴，
∴，
∴，
在和中，
，
∴，
∴，
∴，
故②正确；
如图所示，作于H，于M，

∵和的平分线相交于点O，
∴点O在的平分线上，
∴，
∵，
∴
=
=，
故③正确；
综上，①②③正确，
故选：C．
13．且
解：由题意，得，
解得：且．
故答案为：且．
14．
解：∵，，
∴
，
故答案为：．
15．
解：如图，根据方向角的定义，可得
∴．
∵AE，DB是正南正北方向，
∴，
∵，
又∵，
∴，
∴．
16．8
解：方程去分母得：，
∴
解得，，
∵分式方程的增根为，
∴，
解得，
故答案为：8．
17．3
解：要使△PBG的周长最小，而BG=1一定，只要使BP+PG最短即可，
连接AG交EF于M，
∵等边△ABC，E、F、G分别为AB、AC、BC的中点，
∴AG⊥BC，EF∥BC，
∴AG⊥EF，AM=MG，
∴A、G关于EF对称，
即当P和E重合时，此时BP+PG最小，即△PBG的周长最小，
AP=PG，BP=BE，
最小值是：PB+PG+BG=AE+BE+BG=AB+BG=2+1=3．
故答案为3．
18．①②③
解：如图，作PE⊥OA于E，PF⊥OB于F，
∵∠PEO=∠PFO=90°，
∴∠EPF+∠AOB=180°，
∵∠MPN+∠AOB=180°，
∴∠EPF=∠MPN，
∴∠EPM=∠FPN，
∵OP平分∠AOB，PE⊥OA，PF⊥OB，
∴PE=PF，
在Rt△POE和Rt△POF中，
∵OP=OP，PE=PF，
∴Rt△POE≌Rt△POF（HL），
∴OE=OF，
在△PEM和△PFN中，
∵∠MPE=∠NPF， PE=PF，∠PEM=∠PFN，
∴△PEM≌△PFN（ASA），
∴∠PEM=∠PFN，EM=NF，PM=PN，故①正确；
∴S△PEM=S△PFN，
∴S四边形PMON=S四边形PEOF=定值，故③正确；
∵OM+ON=OE+ME+OF-NF=2OE=定值，故②正确；
∵M，N的位置变化，
∴MN的长度是变化的，
∵PM=PN，∠MPN=60°，
∴△PMN是等边三角形，
∴△PMN的周长是变化的，故④错误，
∴说法正确的有①②③．
故答案为：①②③
19．（1）
（2）
解：（1）原式
．
（2）原式
．
20．（1），3；（2）
解析：（1）
将，代入原式．
（3）解：两边同时乘以得：
，
∴，
解得，
检验：把代入最简公分母得：，
∴是原方程的解．
21．
解析：证明：∵平分，，，
∴，，
∴
∴；
又，，
则，，
∵，
，，
∴四边形的面积为．
22．(1)图形见解析，，，
(2)图形见解析，；面积为8
（1）解：如图所示，即为所求，
∴，，；
（2）解：如图所示，即为所求：
∵点C关于直线对称的点为点，
∴点的坐标为，
∵，，
∴，，
∴．
23．(1)购买一个A材料的吉祥物需50元，购买一个B材料的吉祥物需100元
(2)该学校此次最多可购买10个B材料的吉祥物
（1）解：设购买一个A材料的吉祥物需x元，则购买一个B材料的吉祥物需元，
依题意，得：，
解得：，
经检验，是原方程的解，且符合题意，
∴，
答：购买一个A材料的吉祥物需50元，购买一个B材料的吉祥物需100元；
（2）设该学校此次购买m个B材料的吉祥物，则购买个A材料的吉祥物，
依题意，得：，
解得：．
∴m的最大值为10，
答：该学校此次最多可购买10个B材料的吉祥物．
24．(1)见解析
(2)或
（1）解：证明：若和为关联分式，
则必须满足，
故：，
，
∴，
故分式是分式的“关联分式”；
（2）已知题意：，
①设为P，则其关联式为Q，
，
，
，
，
故其关联式为．
②设为Q，则其关联式为P，
，
，
，
，
故其关联式为．
综上，分式的“关联分式”为或．
25．(1)，
(2)①，理由见解析；②是定值，
（1）解：∵和是等边三角形，
∴，，，
∴，即，
在和中，
，
∴，
∴；
∵线段为边上的中线，是等边三角形，
∴．
故答案为：=，．
（2）①∵和是等边三角形，
∴，，，
∴，即，
在和中，
，
∴，
∴；
②情况一：当点D在线段上时，如图：
∵线段为边上的中线，是等边三角形，
∴，，
∵，
∴，
在中，，
情况二：当点D在线段的延长线上时，如图：
∵线段为边上的中线，是等边三角形，
∴，，
∵，
∴，
在中，，
情况三，当点D在线段的延长线上时，如图：
∵和是等边三角形，
∴，，，
∴，即，
在和中，
，
∴，
∴，
∴
∵线段为边上的中线，是等边三角形，
∴，，
∴，
在中，，
∴的值为定值，．