河北省石家庄市新华区2024-2025学年八年级（上）数学期末模拟测试（含答案及详解）

这是一份河北省石家庄市新华区2024-2025学年八年级（上）数学期末模拟测试（含答案及详解），共24页。试卷主要包含了选择题等内容，欢迎下载使用。
1. 下列防疫的图标中是轴对称图形的是（ ）
A. B. C. D.
2. 下列运算正确是（ ）
A. B. C. D.
3. 人体中枢神经系统中含有1千亿个神经元．某个神经元的直径约为52微米，52微米为5.2 × 10-5米． 将5.2 × 10-5用小数表示为（ ）
A. 0.00052B. 0.000052C. 0.0052D. 0.0000052
4. △ABC中，AB＝3，AC＝2，BC＝a，下列数轴中表示的a的取值范围，正确的是（ ）
A. B.
C. D.
5. 如与的乘积中不含的一次项，则的值为（ ）
A. B. 3C. 0D. 1
6. 若，则2n－3m的值是（ ）
A. －1B. 1C. 2D. 3
7. 现有两根木棒，它们的长是20cm和30cm，若要钉成一个三角形木架，则应选取的第三根木棒长为（ ）
A. 10cmB. 50cmC. 60cmD. 40cm
8. 如图，在 ABC 中，ED / / BC ，ABC 和 ACB 的平分线分别交 ED 于点 G 、F ，若 FG  2 ，ED  6 ,则EB  DC 的值为（ ）
A. 6B. 7
C. 8D. 9
9. 下列关于分式的判断中错误的是（ ）
A. 当时，有意义B. 当时，的值为0
C. 无论x为何值，的值总为正数D. 无论x为何值，不可能得整数值
10. △ABC中，∠C=90°，∠A的平分线交BC于点D，如果AB=8，CD=3，则△ABD的面积为（ ）
A. 24B. 12C. 8D. 6
11. 如图所示，在△ABC中，，，D是BC的中点，连接AD，，垂足为E，则AE的长为（ ）
A. 4B. 6C. 2D. 1
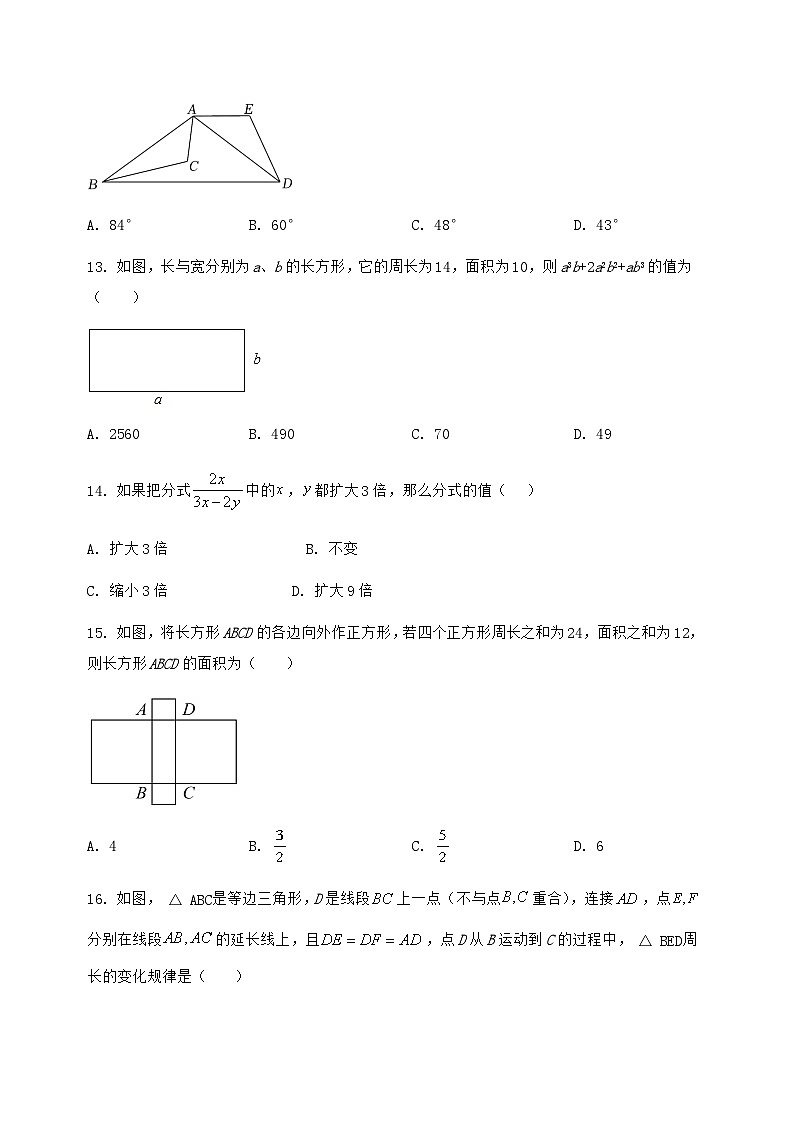
12. 如图，△ABC≌△ADE，且AE∥BD，∠BAD＝94°，则∠BAC的度数的值为（ ）
A. 84°B. 60°C. 48°D. 43°
13. 如图，长与宽分别为a、b的长方形，它的周长为14，面积为10，则a3b+2a2b2+ab3的值为（ ）
A. 2560B. 490C. 70D. 49
14. 如果把分式中的，都扩大3倍，那么分式的值（ ）
A. 扩大3倍B. 不变
C. 缩小3倍D. 扩大9倍
15. 如图，将长方形ABCD的各边向外作正方形，若四个正方形周长之和为24，面积之和为12，则长方形ABCD的面积为（ ）
A. 4B. C. D. 6
16. 如图，△ABC是等边三角形，D是线段上一点（不与点重合），连接，点分别在线段的延长线上，且，点D从B运动到C的过程中，△BED周长的变化规律是（ ）
A. 不变B. 一直变小C. 先变大后变小D. 先变小后变大
二.填空题(本大题共3题，总计 12分)
17. 分解因式：5x4﹣5x2＝________________．
18. 已知在△ABC中，三边长，满足等式，请你探究之间满足的等量关系为__________．
19. 如图，直线a∥b，点M、N分别为直线a和直线b上的点，连接MN，∠DMN=70°，点P是线段MN上一动点，直线DE始终经过点P，且与直线a、b分别交与点D、E，
（1）当△MPD与△NPE全等时，直接写出点P的位置：___________________；
（2）当△NPE是等腰三角形时，则∠NPE的度数为___________________．
三.解答题(共7题，总计66分，解答应写出文字说明、证明过程或演算步骤)
20. （1）计算：
（2）分解因式：
21. 解分式方程：
（1）
（2）
22. 如图，已知△ABC的顶点分别为，，．
（1）作出△ABC关于x轴对称的图形，并写出点的坐标；
（2）若点是内部一点，则点P关于y轴对称的点的坐标是________．
（3）在x轴上找一点P，使得最小（画出图形，找到点P的位置）．
23. 如图，在△ABC中，射线AM平分∠BAC．
（1）尺规作图（不写作法，保留作图痕迹）作BC的中垂线，与AM相交于点G，连接BG、CG；
（2）在（1）条件下，∠BAC和∠BGC有何数量关系？并证明你的结论．
24. 【阅读】下列是多项式因式分解的过程：．请利用上述方法解决下列问题．
【应用】
（1）因式分解：；
（2）若x>5，试比较与0的大小关系；
（3）【灵活应用】若，求的值．
25. 在今年新冠肺炎防疫工作中，某公司购买了、两种不同型号口罩，已知型口罩的单价比型口罩的单价多1.5元，且用8000元购买型口罩的数量与用5000元购买型口罩的数量相同．
（1）、两种型号口罩的单价各是多少元？
（2）根据疫情发展情况，该公司还需要增加购买一些口罩，增加购买型口罩数量是型口罩数量的2倍，若总费用不超过3800元，则增加购买型口罩的数量最多是多少个？
26. 课堂上，老师提出了这样一个问题：如图1，在中，平分交于点D，且．求证：．小明的方法是：如图2，在上截取，使，连接，构造全等三角形来证明结论．
（1）小天提出，如果把小明方法叫做“截长法”，那么还可以用“补短法”通过延长线段构造全等三角形进行证明．辅助线的画法是：延长至F，使_________，连接．请补全小天提出的辅助线的画法，并在图1中画出相应的辅助线；
（2）小芸通过探究，将老师所给的问题做了进一步的拓展，给同学们提出了如下的问题：如图3，点D在的内部，，，分别平分，，，且．求证：．请你解答小芸提出的这个问题；
（3）小东将老师所给问题中的一个条件和结论进行交换，得到的命题如下：如果在中，，点D在边上，，那么平分．小东判断这个命题也是真命题，老师说小东的判断是正确的．请你利用图4对这个命题进行证明．
石家庄市新华区2024-2025学年八年级（上）数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】：C
【解析】：解：轴对称图形定义：把一个图形沿某条直线对折，对折后直线两旁的部分能完全重合．发现A，B，D都不符合定义，所以A，B，D都错误，只有C符合，所以C正确．
故答案为C．
2.【答案】：B
【解析】：A选项，，故不符合题意；
B选项，，故符合题意；
C选项，，故不符合题意；
D选项，，故不符合题意；
故选：B．
3.【答案】：B
【解析】：解：5.2×10-5=0.000052,
故选B
4.【答案】：A
【解析】：解：∵△ABC中，AB＝3，AC＝2，BC＝a，
∴1＜a＜5，
∴A符合，
故选：A．
5.【答案】：A
【解析】：，
又与的乘积中不含的一次项，
，
解得．
故选：A．
6.【答案】：B
【解析】：解：∵，
∴，
∴，
∴．
故选：B
7.【答案】：D
【解析】：解：根据三角形三边关系，
∴三角形的第三边x满足：，即，
故选：D．
8.【答案】：C
【解析】：∵ED∥BC，
∴∠EGB=∠GBC，∠DFC=∠FCB，
∵∠GBC=∠GBE，∠FCB=∠FCD，
∴∠EGB=∠EBG，∠DCF=∠DFC，
∴BE=EG，CD=DF，
∵FG=2，ED=6，
∴EB+CD=EG+DF=EF+FG+FG+DG=ED+FG=8，
故选C．
9.【答案】：D
【解析】：A选项，当时，有意义，故不符合题意；
B选项，当时，的值为0，故不符合题意；
C选项，，则无论x为何值，的值总为正数，故不符合题意；
D选项，当时，，故符合题意；
故选：D．
10.【答案】：B
【解析】：作DE⊥AB于E，
∵AD平分∠BAC，DE⊥AB，DC⊥AC，
∴DE=CD=3，
∴△ABD的面积为×3×8=12，
故选：B．
11.【答案】：C
【解析】：解： ， ，D为BC中点，
，
，
，D为BC中点，
，
，
， ，
，
．
故答案为：C．
12.【答案】：D
【解析】：∵△ABC≌△ADE，∠BAD＝94°，
∴AB＝AD，∠BAC＝∠DAE，
∴∠ABD＝∠ADB＝×（180°﹣94°）＝43°，
∵AE//BD，
∴∠DAE＝∠ADB＝43°，
∴∠BAC＝∠DAE＝43°．
故选：D．
13.【答案】：B
【解析】：解：∵长与宽分别为a、b的长方形，它的周长为14，面积为10，
∴ab＝10，a+b＝7，
∴a3b+2a2b2+ab3＝ab（a+b）2＝10×72＝490．
故选：B．
14.【答案】：B
【解析】：．
故选：B．
【画龙点睛】本题考查了分式的性质，分式的分子分母都乘以或除以同一个不为0的整式，分式的值不变．
15.【答案】：B
【解析】：解：设AB＝a，AD＝b，由题意得8a＋8b＝24，2a2＋2b2＝12，
即a＋b＝3，a2＋b2＝6，
∴，
即长方形ABCD的面积为，
故选：B．
16.【答案】：D
【解析】：∵△ABC是等边三角形，
，
，
，
，
又，
，
，
，
，
在和中，，
，
，
则△BED周长为，
在点D从B运动到C的过程中，BC长不变，AD长先变小后变大，其中当点D运动到BC的中点位置时，AD最小，
在点D从B运动到C的过程中，周长的变化规律是先变小后变大，
故选：D．
二. 填空题
17.【答案】： 5x2（x＋1）（x－1）
【解析】：5x4-5x2=5x2（x2-1）
=5x2（x+1）（x-1）．
故答案为：5x2（x+1）（x-1）．
18.【答案】：
【解析】：∵，
∴，
∴，
∴
∵，
∴，
∴，
故答案为：
19.【答案】： ①. MN中点处 ②. 70°或40°或55°
【解析】：（1）∵a//b
∴∠DMN=∠PNE，∠MDE=∠DEN，
∴当△MPD与△NPE全等时，即△MPD≌△NPE时MP=NP，
即点P是MN的中点．
故答案为：MN中点处
（2）①若PN=PE时，
∵∠DMN=∠PNE=70°，
∴∠DMN =∠PNE=∠PEN=70°．
∴∠NPE=180°-∠PNE-∠PEN=180°-70°-70°=40°．
∴∠NPE =40°；
②若EP=EN时，则∠NPE =∠PNE=∠DMN =70°；
③若NP=NE时，则∠PEN=∠NPE，此时2∠NPE=180°-∠PNE=180°-∠DMN =180°-70°=110°
∴∠NPE =55°；
综上所述，∠NPE的值是40°或70°或55°．
故答案为：40°或70°或55°．
三.解答题
20【答案】：
（1）
（2）
【解析】：
【小问1详解】
解：原式；
【小问2详解】
解：原式．
【画龙点睛】本题考查了整式的混合运算、因式分解，熟练掌握运算法则是解题的关键．
21【答案】：
（1）
（2）无解
【解析】：
【小问1详解】
解：方程两边同乘以得，
解这个整式方程，得，
检验：将代入最简公式分母，
原分式方程的解为．
【小问2详解】
将方程两边同时乘以得：
，
解这个整式方程，得：，
将代入，
所以是增根，
所以原分式方程无解．
【画龙点睛】本题考查的是分式方程的求解，解题的关键是将分式方程转化为整式方程，易错点是漏乘不含未知数的项．
22【答案】：
（1）图见解析，点的坐标为；
（2）；
（3）见解析．
【解析】：
（1）分别找出A，B，C关于x轴对称的点A1，B1，C1，再顺次连接点即可；
（2）利用“关于谁对称谁不变，不关谁对称谁全变”可求出P的对称点坐标；
（3）过x轴作点A的对称点为A1，连接A1C交于x轴的点即为点P，使得最小．
【小问1详解】
解：先找出点A，B，C关于x轴对称的点A1，B1，C1，再顺次连接A1，B1，C1．
如图所示，即为所求：
的坐标为．
【小问2详解】
解：∵P关于y轴对称，则纵坐标不变，横坐标变成原来的相反数，
∴点P关于y轴对称的点的坐标是．
【小问3详解】
解：过x轴作点A的对称点为A1，连接A1C交于x轴的点即为点P，使得最小．点P如图所示：
【画龙点睛】本题考查作轴对称图形，找关于坐标轴对称的点的坐标，以及动点问题．关键是掌握画轴对称图形的方法：先找对称点，再连线；熟记关于坐标轴对称的点的坐标变化特征；利用对称性解决动点问题．
23【答案】：
（1）详见解析；（2）∠BAC+∠BGC＝180°，证明详见解析．
【解析】：
解：（1）线段BC的中垂线EG如图所示：
（2）结论：∠BAC+∠BGC＝180°．
理由：在AB上截取AD＝AC，连接DG．
∵AM平分∠BAC，
∴∠DAG＝∠CAG，
在△DAG和△CAG中
∵
∴△DAG≌△CAG（SAS），
∴∠ADG＝∠ACG，DG＝CG，
∵G在BC的垂直平分线上，
∴BG＝CG，
∴BG＝DG，
∴∠ABG＝∠BDG，
∵∠BDG+∠ADG＝180°，
∴∠ABG+∠ACG＝180°，
∵∠ABG+∠BGC+∠ACG+∠BAC＝360°，
∴∠BAC+∠BGC＝180°．
24【答案】：
（1）
（2）
（3）5
【解析】：
【小问1详解】
解：，
【小问2详解】
解：，，
∴x+1＞0，x-5＞0，
，
；
【小问3详解】
解：，
，
∵，
∴，
∴a=1，，
．
25【答案】：
（1）型口罩单价为4元/个，型口罩单价为2.5元/个；
（2）增加购买型口罩的数量最多是422个
【解析】：
（1）设型口罩单价为元/个，则型口罩单价为元/个，
根据题意，得：，解方程，得，
经检验：是原方程的根，且符合题意，∴（元），
答：型口罩单价为4元/个，型口罩单价为2.5元/个；
（2）设增加购买型口罩的数量是个，则增加购买型口罩数量是2个，
根据题意，得：，
解不等式，得：，
∵为正整数，∴正整数的最大值为422，
答：增加购买型口罩的数量最多是422个．
【画龙点睛】本题考查了分式方程和不等式的应用，属于常考题型，正确理解题意、找准相等与不等关系是解题的关键．
26【答案】：
（1）BD，证明见解析；（2）见解析；（3）见解析．
【解析】：
（1）延长AB至F，使BF＝BD，连接DF，根据三角形的外角性质得到∠ABC＝2∠F，则可利用SAS证明△ADF≌△ADC，根据全等三角形的性质可证明结论；
（2）在AC上截取AE，使AE＝AB，连接DE，则可利用SAS证明△ADB≌△ADE，根据全等三角形的性质即可证明结论；
（3）延长AB至G，使BG＝BD，连接DG，则可利用SSS证明△ADG≌△ADC，根据全等三角形的性质、角平分线的定义即可证明结论．
【详解】证明：（1）如图1，延长AB至F，使BF＝BD，连接DF，
则∠BDF＝∠F，
∴∠ABC＝∠BDF＋∠F＝2∠F，
∵AD平分∠BAC
∴∠BAD＝∠CAD，
∵AB＋BD＝AC，BF＝BD，
∴AF＝AC，
在△ADF和△ADC中，
，
∴△ADF≌△ADC（SAS），
∴∠ACB＝∠F ，
∴∠ABC＝2∠ACB．
故答案为：BD．
（2）如图3，在AC上截取AE，使AE＝AB，连接DE，
∵AD，BD，CD分别平分∠BAC，∠ABC，∠ACB，
∴∠DAB＝∠DAE，∠DBA＝∠DBC，∠DCA＝∠DCB，
∵AB＋BD＝AC，AE＝AB，
∴DB＝CE，
△ADB和△ADE中，
，
∴△ADB≌△ADE（SAS），
∴BD＝DE，∠ABD＝∠AED，
∴DE＝CE，
∴∠EDC＝∠ECD，
∴∠AED＝2∠ECD，
∴∠ABD＝2∠ECD，
∴∠ABC＝2∠ACB．
（3）如图4，延长AB至G，使BG＝BD，连接DG，
则∠BDG＝∠AGD，
∴∠ABC＝∠BDG＋∠AGD＝2∠AGD，
∵∠ABC＝2∠ACB，
∴∠AGD＝∠ACB，
∵AB＋BD＝AC，BG＝BD，
∴AG＝AC，
∴∠AGC＝∠ACG，
∴∠DGC＝∠DCG，
∴DG＝DC，
在△ADG和△ADC中，
，
∴△ADG≌△ADC（SSS），
∴∠DAG＝∠DAC，即AD平分∠BAC．
【画龙点睛】本题考查的是三角形全等的判定和性质、角平分线的定义，掌握全等三角形的判定定理和性质定理是解题的关键．