

所属成套资源:河北省各地区2024-2025学年八年级(上)数学期末模拟测试(含答案及详解)
河北省正定县2024-2025学年八年级(上)数学期末模拟测试(含答案及详解)
展开
这是一份河北省正定县2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共22页。试卷主要包含了选择题等内容,欢迎下载使用。
1. 用数学的眼光观察下面的网络图标,其中可以抽象成轴对称图形的是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B.
C. D.
3. 冠状病毒是一个大型病毒家族,借助电子显微镜,我们可以看到这些病毒直径约为125纳米(1纳米米),125纳米用科学记数法表示等于( )
A. 米B. 米C. 米D. 米
4. 已知正多边形的一个内角是135°,则这个正多边形的边数是( )
A. 3B. 4C. 6D. 8
5. 若M=(x-3)(x-4),N=(x-1)(x-6),则M与N的大小关系为()
A. M>NB. M=NC. M<ND. 由x的取值而定
6. 分式﹣可变形为( )
A. ﹣B. C. ﹣D.
7. 下列等式中,不成立的是( )
A. B.
C. D.
8. 下列关于分式的判断中错误的是( )
A. 当时,有意义B. 当时,的值为0
C. 无论x为何值,的值总为正数D. 无论x为何值,不可能得整数值
9. 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
A. 60°B. 50°C. 40°D. 30°
10. 点在的角平分线上,点到边的距离等于,点是边上的任意一点,则下列选项正确的是( )
A. B. C. D.
11. 如图,已知∠ABD=∠BAC,添加下列条件还不能判定△ABC≌△BAD的依据是( )
A. AC=BDB. ∠DAB=∠CBAC. ∠C=∠DD. BC=AD
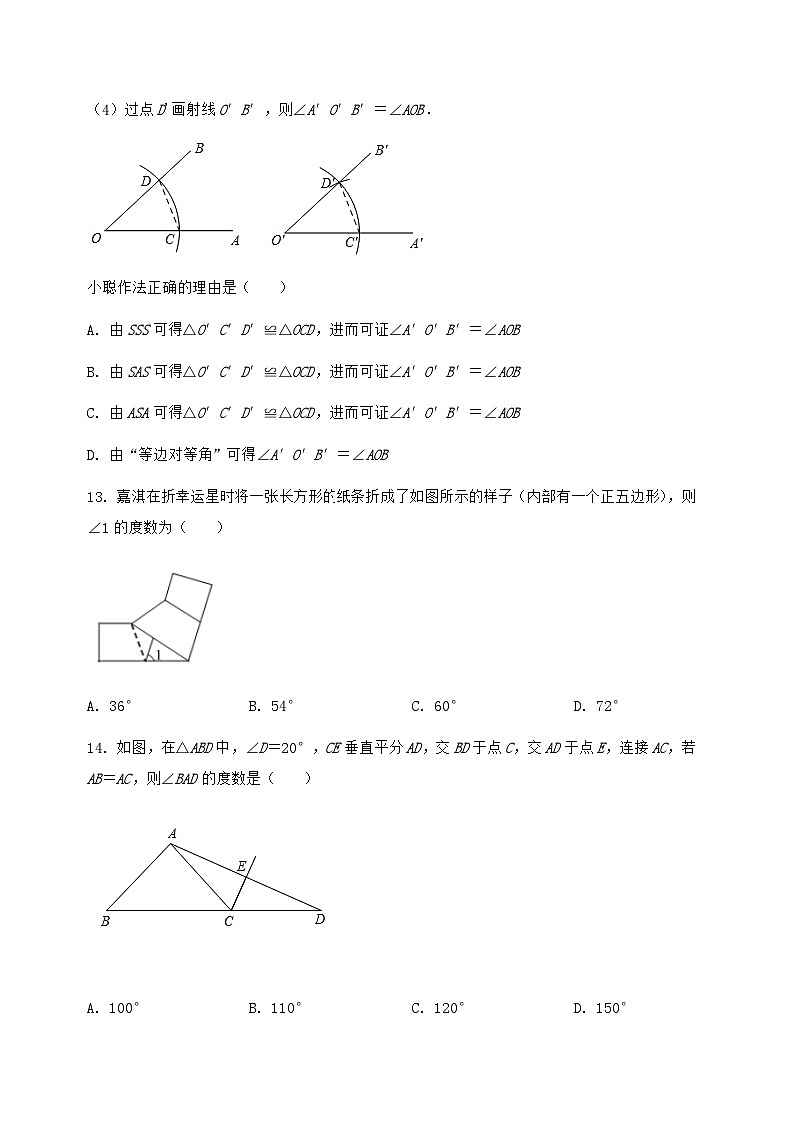
12. 为半径画弧,交O′A′于点C′;
(3)以点C'为圆心,CD长为半径画弧,与第(2)步中所画的弧相交于点D′;
(4)过点D'画射线O′B′,则∠A′O′B′=∠AOB.
小聪作法正确的理由是( )
A. 由SSS可得△O′C′D′≌△OCD,进而可证∠A′O′B′=∠AOB
B. 由SAS可得△O′C′D′≌△OCD,进而可证∠A′O′B′=∠AOB
C. 由ASA可得△O′C′D′≌△OCD,进而可证∠A′O′B′=∠AOB
D. 由“等边对等角”可得∠A′O′B′=∠AOB
13. 嘉淇在折幸运星时将一张长方形纸条折成了如图所示的样子(内部有一个正五边形),则∠1的度数为( )
A. 36°B. 54°C. 60°D. 72°
14. 如图,在△ABD中,∠D=20°,CE垂直平分AD,交BD于点C,交AD于点E,连接AC,若AB=AC,则∠BAD的度数是( )
A. 100°B. 110°C. 120°D. 150°
15. 已知甲、乙、丙均为x的一次多项式,且其一次项系数皆为正整数,若甲与乙相乘得,乙与丙相乘得,则甲、丙之积与乙的差是( )
A. B.
C. D.
16. 已知关于x的分式方程无解,则k的值为( )
A. 0B. 0或-1C. -1D. 0或
二.填空题(本大题共3题,总计 12分)
17. 若,则分式__.
18. 如图,△ABC中,是的垂直平分线,AE=3cm, △ABD的周长为,则的周长为______.
19. 已知△ABC是等边三角形,点D在射线BC上(与点B,C不重合),点D关于直线的对称点为点E.
(1)如图1,连接,,,当时,根据边的关系,可判定的形状是___________三角形;
(2)如图2,当点D在延长线上时,连接,,,,延长到点G,使,连接,交于点F,F为的中点.若,则的长为___________.
三.解答题(共7题,总计66分,解答应写出文字说明、证明过程或演算步骤)
20. (1)计算:
(2)分解因式:
21. 已知(x+y)2=1,(x﹣y)2=49,求x2+y2与y的值.
22. 如图,△ABC三个顶点的坐标分别为A(﹣4,﹣2),B(﹣1,﹣1),C(﹣1,﹣4).
(1)画出△ABC关于y轴对称的图形△A1B1C1;
(2)在x轴上作出一点P,使PA+PB的值最小(保留作图痕迹)
23. 已知在△ABC中,,,是△ABC的高,分别交,于点E,F.
(1)如图1,若,且,求的度数;
(2)如图2,若.
①求的度数;
②求证:.
24. 阅读以下材料
材料:因式分解:
解:将“”看成整体,令,则原式
再将“A”还原,得原式
上述解题用到是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你解答下列问题:
(1)因式分解:______;
(2)因式分解:;
25. 某车间有甲乙两个小组,甲组的工作效率比乙组的工作效率高20%,甲组加工2700个零件所用的时间比乙组加工2000个零件所用的时间多半小时,求甲乙两组每小时各加工零件多少个?
26. 已知M是等边△ABC的边BC上的点.
(1)如图①,过点M作MN∥CA,交AB于点N,求证:BM = BN;
(2)如图②,连接AM,过点M作∠AMH = 60°,MH与∠ACB的邻补角的平分线交于点H,过点H作HD⊥BC,交BC延长线于点D.
(ⅰ)求证:MA = MH;
(ⅱ)直接写出CB,CM,CD之间的数量关系式.
正定县2024-2025学年八年级(上)数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】:C
【解析】:解:选项不是轴对称图形,故不符合题意;
选项不是轴对称图形,故不符合题意;
选项是轴对称图形,故符合题意;
选项不是轴对称图形,故不符合题意;
故选:
2.【答案】:D
【解析】:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项正确,符合题意;
故选:D.
3.【答案】:A
【解析】:解:125纳米=125×10-9米=米,
故选:A.
4.【答案】:D
【解析】:解:∵正多边形的一个内角是135°,
∴该正多边形的一个外角为45°,
∵多边形的外角之和为360°,
∴边数=,
∴这个正多边形的边数是8.
故选:D.
5.【答案】:A
【解析】:解: M=(x-3)(x-4)=
N=(x-1)(x-6)=
即:
故选:A.
6.【答案】:B
【解析】: 可变式为
∴B正确
故选B
7.【答案】:C
【解析】:A、,故A不符合题意.
B、,故B不符合题意.
C、,故C符合题意.
D、,故D不符合题意.
故选:C.
8.【答案】:D
【解析】:A选项,当时,有意义,故不符合题意;
B选项,当时,的值为0,故不符合题意;
C选项,,则无论x为何值,的值总为正数,故不符合题意;
D选项,当时,,故符合题意;
故选:D.
9.【答案】:C
【解析】:解:∵FE⊥DB,
∵∠DEF=90°,
∵∠1=50°,
∴∠D=90°﹣50°=40°,
∵AB∥CD,
∴∠2=∠D=40°.
故选C.
10.【答案】:B
【解析】:∵点P在∠AOB的平分线上,点P到OA边的距离等于5,
∴点P到OB的距离为5,
∵点Q是OB边上的任意一点,
∴PQ≥5.
故选:B.
11.【答案】:D
【解析】:由题意得,∠ABD=∠BAC,
A.在△ABC与△BAD中,
,
∴△ABC≌△BAD(SAS);
故选项正确;
B.在△ABC与△BAD中,
,
△ABC≌△BAD(ASA),
故选项正确;
C.在△ABC与△BAD中,
,
△ABC≌△BAD(AAS),
故选项正确;
D.在△ABC与△BAD中,
BC=AD,AB=BA,∠BAC=∠ABD(SSA),△ABC与△BAD不全等,故错误;
故选:D.
12.【答案】:A
【解析】:解:由作图得OD=OC=OD′=OC′,CD=C′D′,
则根据“SSS”可判断△C′O′D′≌△COD.
故选:A.
13.【答案】:D
【解析】:∵折的图形为正五边形,
∴∠2= =108°,
又∵长方形纸片对边平行,
∴∠1+∠2=180°,
∠1=180°-∠2=180°-108°=72°
故选D.
14.【答案】:C
【解析】:解:∵CE垂直平分AD,
∴,
∴,
∴,
∵AB=AC,
∴,
∴,
∴,
故选:C.
15.【答案】:A
【解析】:A
∵,
∵,
又∵甲与乙相乘得:,乙与丙相乘得:,
∴甲为,乙为,丙为,
∴甲、丙之积与乙的差是:
,
,
,
故选:A
16.【答案】:D
【解析】:解:分式方程去分母得: ,即 ,
当,即 时,方程无解;
当x=-1时,-3k+1=-3k,此时k无解;
当x=0时,0=-3k,k=0,方程无解;
综上,k的值为0或 .
故答案为:D.
二. 填空题
17.【答案】: 1
【解析】:原分式,
,
.
故答案为:1.
18.【答案】: 19cm
【解析】:解:∵是的垂直平分线,
∴cm,,
∴AC=AE+CE=6(cm),
∵的周长为,
∴(cm),
∴(cm),即(cm),
∴(cm);
∴△ABC的周长为19cm;
故答案为:19cm.
19.【答案】: ①. 等边 ②. 6
【解析】:(1)△ADE是等边三角形,理由如下:
点D, E关于直线AC对称,
AD=AE,∠DAC=∠EAC,
∵△ABC是等边三角形,
AB=AC,∠BAC=60°,
点D为线段BC的中点,
,
,
∠DAE=60°,
AD=AE,
△ADE是等边三角形;
(2)解:如图2所示,.
证明: F为线段BE的中点,
BF=EF,
∵△ABC是等边三角形,
AC=BC, ,
,
点D, E关于直线AC对称,
CD=CE,∠ACD=∠ACE=120°,
, ,
CE=BG,∠BCE=60°,
,,
,
在△BFG和△EFC中,
∴△BFG≌△EFCSAS ,
,
CG=2CF,
在 和 中,
,
∴△ACD≌△CBGSAS ,
AD=CG,
,
,
;
故答案为:等边;6.
三.解答题
20【答案】:
(1)
(2)
【解析】:
【小问1详解】
解:原式;
【小问2详解】
解:原式.
【画龙点睛】本题考查了整式的混合运算、因式分解,熟练掌握运算法则是解题的关键.
21【答案】:
,的值为或或或
【解析】:
解:∵①,②,
∴①+②得:,解得;
∵,
或,
,
或,
或或或,
解得或或或,
,的值为或或或.
【画龙点睛】此题考查了完全平方公式、平方根的运用,熟练掌握完全平方公式和平方根的运算是解本题的关键.
22【答案】:
(1)见解析.
(2)见解析
【解析】:
【小问1详解】
解:A1(4,﹣2),B1(1,﹣1),C1(1,﹣4).
如图所示:△A1B1C1,即为所求;
【小问2详解】
解:如图所示:点P即为所求.
【画龙点睛】本题主要考查了轴对称变换以及利用轴对称求最短路线,正确得出对应点位置是解题关键.
23【答案】:
(1)30° (2)①;②见解析
【解析】:
【小问1详解】
∵BF⊥AC,
∴∠AFB=90°,
∵∠BAC=45°,
∴∠ABF=90°-∠BAC=45°,
∵∠BDE=75°,
∴∠BAE=∠BDE-∠ABF=30°;
【小问2详解】
①∵∠ABC=∠C,
∴AB=AC,
∵AE⊥BC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC=22.5°;
②证明:∵∠BAC=45°,BF⊥AC,
∴∠AFB=90°,
∴∠ABF=∠BAC=45°,
∴FA=FB,
∵BF⊥AC,AE⊥BC,
∴∠CFB=∠AFD=∠AEC=90°,
∴∠C+∠CAE=90°,∠ADF+∠CAE=90°,
∴∠ADF=∠C,
在△ADF和△BCF中,
,
∴△ADF≌△BCF(AAS).
24【答案】:
(1)
(2)
【解析】:
【小问1详解】
解:
=
=;
故答案为:;
【小问2详解】
设,
原式,
将A还原,则原式;
25【答案】:
甲每小时加工600个零件,乙每小时加工500个零件
【解析】:
解:设乙组每小时加工的零件数为x个,则甲组每小时加工零件数为
(1+20%)x个.根据题意得:
=+,
解得:x=500,
经检验,x=500是原方程的解,
(1+20%)x=600,
答:甲每小时加工600个零件,乙每小时加工500个零件.
26【答案】:
(1)见解析 (2)(ⅰ)见解析;(ⅱ)BC CM 2CD
【解析】:
∴△AMN≌△MHC(ASA),
∴MA=MH;
(ⅱ)CB=CM+2CD;理由如下:
证明:如图2,过M点作MG⊥AB于G,
∵△AMN≌△MHC,
∴MN=HC,
∵△BMN为等边三角形,MG⊥AB
∴MN=MB,BM=2BG,
∴HC=BM,
△BMG和△CHD中
&∠B=∠HCD&∠MGB=∠HDC&HC=MB,
∴△BMG≌△CHD(AAS),
∴CD=BG,
∴BM=2CD,
所以BC=MC+2CD.
【画龙点睛】此题主要考查了等边三角形的性质,以及全等三角形的判定与性质,关键是正确作出辅助线,熟练掌握证明三角形全等的方法.
相关试卷
这是一份河北省无极县2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共22页。试卷主要包含了选择题等内容,欢迎下载使用。
这是一份河北省安国市2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共19页。试卷主要包含了选择题等内容,欢迎下载使用。
这是一份河北省威县2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共22页。试卷主要包含了选择题等内容,欢迎下载使用。









