



所属成套资源:人教版数学八年级上册期末高分训练(原卷+解析)
人教版数学八上高分突破训练专项09 平行+线段中点构造全等模型综合应用(2份,原卷版+解析版)
展开
这是一份人教版数学八上高分突破训练专项09 平行+线段中点构造全等模型综合应用(2份,原卷版+解析版),文件包含人教版数学八上高分突破训练专项09平行+线段中点构造全等模型综合应用原卷版doc、人教版数学八上高分突破训练专项09平行+线段中点构造全等模型综合应用解析版doc等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
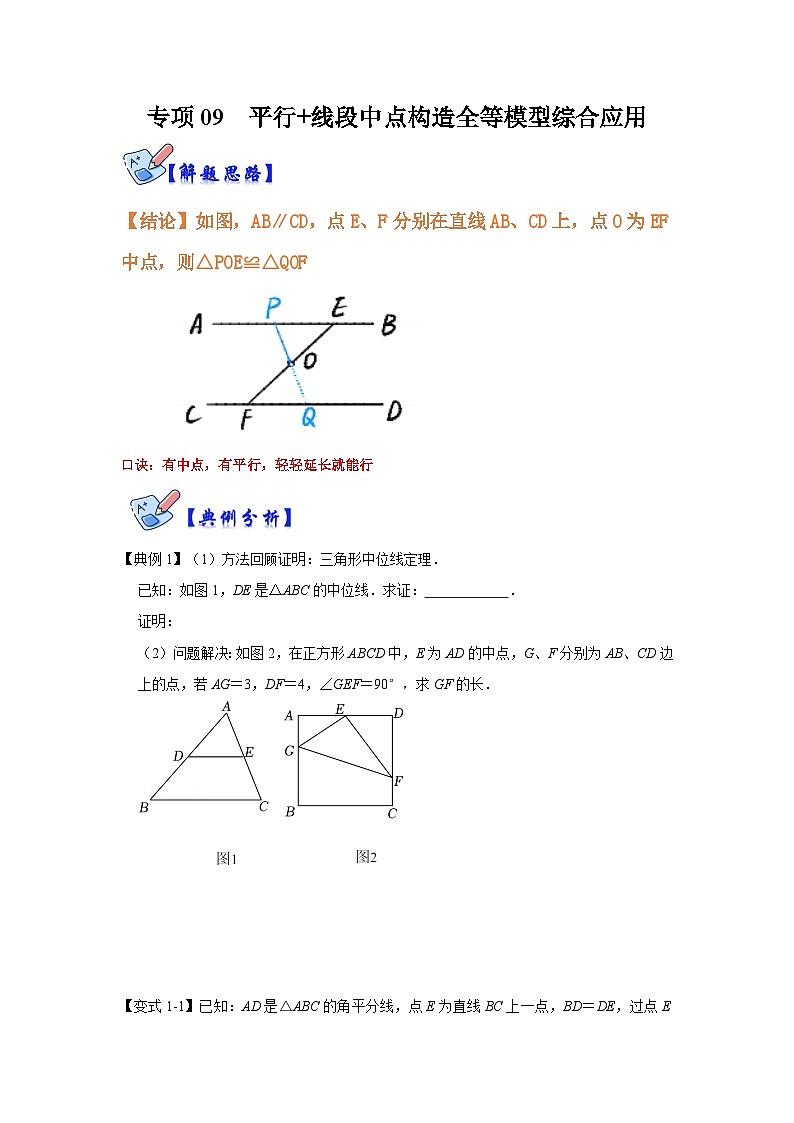
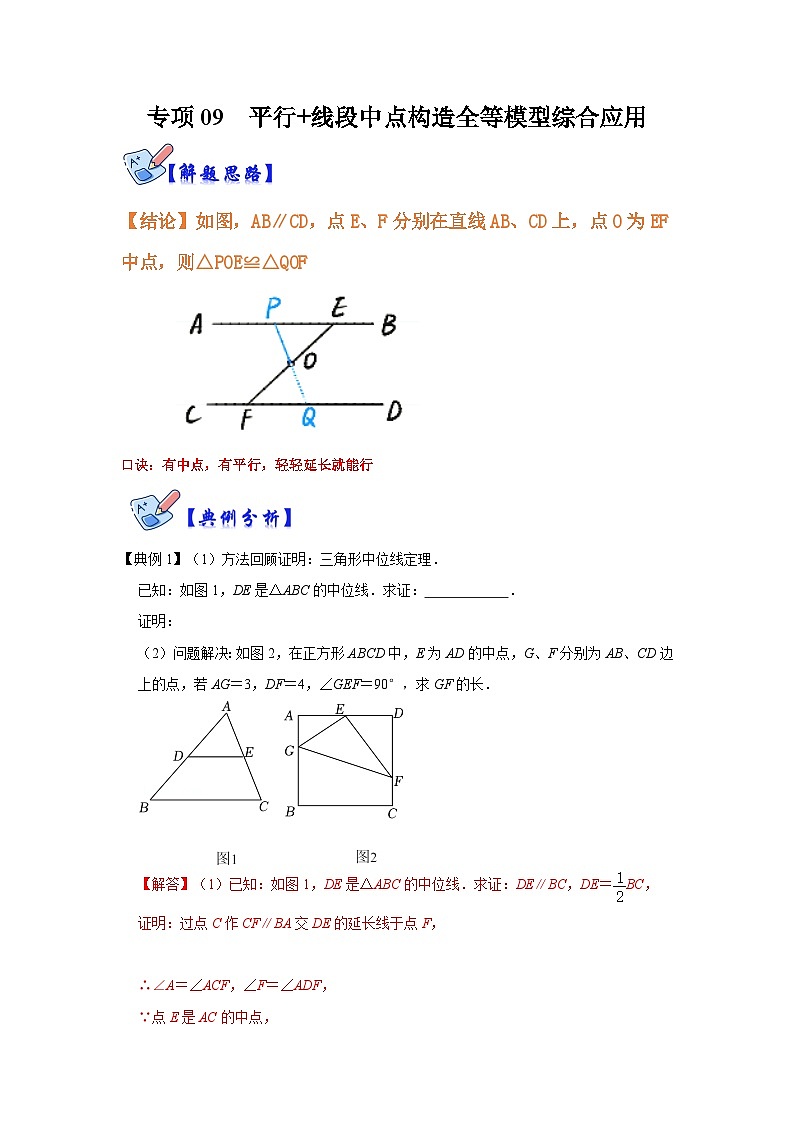
【结论】如图,AB∥CD,点E、F分别在直线AB、CD上,点O为EF中点,则△POE≌△QOF
口诀:有中点,有平行,轻轻延长就能行
【典例1】(1)方法回顾证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.求证: .
证明:
(2)问题解决:如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3,DF=4,∠GEF=90°,求GF的长.
【解答】(1)已知:如图1,DE是△ABC的中位线.求证:DE∥BC,DE=BC,
证明:过点C作CF∥BA交DE的延长线于点F,
∴∠A=∠ACF,∠F=∠ADF,
∵点E是AC的中点,
∴AE=EC,
∴△ADE≌△CFE(AAS),
∴DE=EF=DF,AD=CF,
∵点D是AB的中点,
∴AD=DB,
∴DB=CF,
∴四边形DBCF是平行四边形,
∴DF∥BC,DF=BC,
∴DE∥BC,DE=BC,
故答案为:DE∥BC,DE=BC;
(2)延长GE,CD交于点H,
∵四边形ABCD是正方形,
∴AB∥CD,
∴∠A=∠ADH,∠AGE=∠H,
∵点E是AD的中点,
∴AE=DE,
∴△AGE≌△DHE(AAS),
∴AG=DH=3,GE=EH,
∵DF=4,
∴FH=DH+DF=7,
∵∠GEF=90°,
∴FE是GH的垂直平分线,
∴GF=FH=7,
∴GF的长为7.
【变式1-1】已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图③.写出AF、EF与AB的数量关系,并对图②进行证明.
【解答】(1)证明:如图①,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG+EF=AF+EF,
∴AF+EF=AB;
(2)结论:AF﹣EF=AB.
证明:如图②,延长AD、EF交于点G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠G=∠BAD,
∴∠G=∠CAD,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(AAS),
∴AB=GE,
∵GE=FG﹣EF=AF﹣EF,
∴AF﹣EF=AB;
(3)结论:EF﹣AF=AB.
证明:如图③,延长AD交EF于点G,
∵AD平分∠PAC,
∴∠PAD=∠CAD,
∵EF∥AB,
∴∠AGF=∠PAD,
∴∠AGF=∠CAD,∠ABD=∠GED,
∴FG=AF,
在△ABD和△GED中,
,
∴△ABD≌△GED(ASA),
∴AB=GE,
∵EF﹣FG=GE,
∴EF﹣AF=AB;
【变式1-2】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA⊥OC.
(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
【解答】解:
(1)如图,延长AO交CD的延长线于点E,
∵O为BD的中点,
∴BO=DO,
在△AOB与△EOD中,
∴△AOB≌△EOD,(ASA)
∴AO=AE,
又∵OA⊥OC,
∴AC=CE
∴CO平分∠ACD;(三线合一)
(2)由△AOB≌△EOD
可得AB=DE
∴AB+CD=CD+DE=CE
∵AC=CE
∴AB+CD=AC
1.如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.
(1)求证:△ADE≌△BFE.
(2)连接EM,如果FM=DM,判断EM与DF的关系,并说明理由.
【解答】(1)证明:∵AD∥BC,
∴∠ADE=∠BFE,
∵E为AB的中点,
∴AE=BE,
在△AED和△BFE中,,
∴△AED≌△BFE(AAS);
(2)解:EM与DM的关系是EM垂直且平分DF;理由如下:
连接EM,如图所示:
由(1)得:△AED≌△BFE,
∴DE=EF,
∵∠MDF=∠ADF,∠ADE=∠BFE,
∴∠MDF=∠BFE,
∴FM=DM,
∴EM⊥DF,
∴ME垂直平分DF.
2.△ABC中,P是BC边上的一点,过P作直线交AB于M,交AC的延长线于N,且PM=PN,MF∥AN,
(1)求证:△PMF≌△PNC;
(2)若AB=AC,求证:BM=CN.
【解答】(1)证明:∵MF∥AN,
∴∠MFP=∠NCP,
在△PMF和△PNC中,
,
∴△PMF≌△PNC(AAS);
(2)证明:由(1)得:△PMF≌△PNC,
∴FM=CN,
∵AB=AC,
∴∠B=∠ACB,
∵MF∥AN,
∴∠MFB=∠ACB,
∴∠B=∠MFB,
∴BM=FM,
∴BM=CN.
3.如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
(3)求证:AD+BG=DG.
【解答】解:(1)如图1,∵E是AB的中点,
∴AE=BE,
∵AD∥BC,
∴∠A=∠ABF,∠ADE=∠F,
∴△ADE≌△BFE;
(2)如图2,EG⊥DF,理由是:
∵∠ADF=∠F,∠ADF=∠GDF,
∴∠F=∠GDF,
∴DG=FG,
由(1)得:△ADE≌△BFE,
∴DE=EF,
∴EG⊥FD;
(3)如图2,由(1)得:△ADE≌△BFE,
∴AD=BF,
∵FG=BF+BG,
∴FG=AD+BG,
∵FG=DG,
∴AD+BG=DG.
4.如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求AE的长.
【解答】解:如图,延长AE交BC于F.
∵AB⊥BC,AB⊥AD,
∴AD∥BC
∴∠D=∠C,∠DAE=∠CFE,
又∵点E是CD的中点,
∴DE=CE.
∵在△AED与△FEC中,
,
∴△AED≌△FEC(AAS),
∴AE=FE,AD=FC.
∵AD=5,BC=10.
∴BF=5
在Rt△ABF中,,
∴AE=AF=6.5.
5.阅读理解
(1)如图①,△ABC中,D是BC中点,连接AD,直接回答S△ABD与S△ADC相等吗? 相等 (S表示面积);
应用拓展
(2)如图②,已知梯形ABCD中,AD∥BC,E是AB的中点,连接DE、EC,试利用上题得到的结论说明S△DEC=S△ADE+S△EBC;
解决问题
(3)现有一块如图③所示的梯形试验田,想种两种农作物做对比实验,用一条过D点的直线,将这块试验田分割成面积相等的两块,画出这条直线,并简单说明另一点的位置.
【解答】解:(1)如图①,过点A作AE⊥BC于E.
∵D是BC中点,
∴BD=CD,
又∵S△ABD=•BD•AE,S△ADC=•CD•AE,
∴S△ABD=S△ADC.
故答案为相等;
(2)如图②,延长DE交CB的延长线于点F.
∵E是AB的中点,∴AE=BE.
∵AD∥BC,∴∠ADE=∠BFE.
在△DAE与△FBE中,
,
∴△DAE≌△FBE(AAS),
∴DE=FE,S△DAE=S△FBE,
∴E是DF中点,
∴S△DEC=S△FEC=S△BFE+S△EBC=S△ADE+S△EBC,
∴S△DEC=S△ADE+S△EBC;
(3)如图所示:
取AB的中点E,连接DE并延长,交CB的延长线于点F,取CF的中点G,作直线DG,
则直线DG即可将这块试验田分割成面积相等的两块.
6.如图,直角△ABC,∠ABC=90°,分别以AB、AC为直角边作等腰直角△ABD、△ACE,连接DE交AB于F,求证:BC=2AF.
【解答】证明:在AB上取点M,使AM=BC,连接DM,
∵△ABD是等腰直角三角形,
∴AB=AD,∠BAD=90°,
∴∠ABC=∠DAM,
∴△ABC≌△DAM(SAS),
∴AC=DM,∠AMD=∠ACB,
∵AC=AE,
∴AE=DM,
∵∠ACB=∠DAC,
∴∠AMD=∠DAC,
∵∠CAE=∠DAB=90°,
∴∠DAN=∠BAE,
∴∠AMD=∠BAE,
∵∠AFE=∠DFM,
∴△DMF≌△EAF(AAS),
∴AF=FM,
∴BC=AM=2AF.
7.如图,梯形ABCD中,AD∥BC,E是CD的中点,AE平分∠BAD,AE⊥BE.
(1)求证:BE平分∠ABC;
(2)求证:AD+BC=AB;
(3)若S△ABE=4,求梯形ABCD的面积.
【解答】(1)证明:延长AE交BC的延长线于M,如图所示:
∵AD∥BC,
∴∠M=∠DAE,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠M,
∴AB=MB,
∵AE⊥BE,
∴∠ABE=∠CBE,
∴BE平分∠ABC;
(2)证明:∵AB=MB,BE⊥AE,
∴AE=ME,
∵E是CD的中点,
∴DE=CE,
在△ADE和△MCE中,,
∴△ADE≌△MCE(SAS),
∴AD=MC,
∴AD+BC=MC+BC=MB=AB;
(3)解:∵AB=MB,AE=ME,
∴△MBE的面积=△ABE的面积=4,
∴△ABM的面积=2×4=8,
∵△ADE≌△MCE,
∴△ADE的面积=△MCE的面积,
∴梯形ABCD的面积=△ABM的面积=8.
8.如图,在梯形ABCD中,AD∥BC,E是AB的中点.
(1)求证:S△CED=S△ADE+S△BCE.
(2)当CE=DE时,判断BC与CD的位置关系,并说明理由.
【解答】(1)证明:延长DE交CB的延长线于F,
∵AD∥CF,
∴∠A=∠ABF,∠ADE=∠F,
∵E是AB中点,
∴AE=BE,
在△AED与△BEF中,
,
∴△AED≌△BEF(AAS),
∴DE=EF,S△AED=S△EBF,
∴S△DEC=S△EFC=S△ADE+S△BCE.
(2)解:当CE=DE时,BC⊥CD.
理由:
∵△AED≌△BEF,
∴DE=EF,
∵CE=DE,
∴CE=DE=EF,
∴∠F=∠ECF,∠ECD=∠CDE,
∵∠F+∠ECF+∠ECD+∠CDE=180°,
∴∠FCD=90°,
∴BC⊥CD.
相关试卷
这是一份人教版数学八上高分突破训练专项12 角平分线+垂直构造全等模型综合应用(2份,原卷版+解析版),文件包含人教版数学八上高分突破训练专项12角平分线+垂直构造全等模型综合应用原卷版doc、人教版数学八上高分突破训练专项12角平分线+垂直构造全等模型综合应用解析版doc等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
这是一份人教版数学八上高分突破训练专项11 用截长补短法构造全等三角形综合应用(2份,原卷版+解析版),文件包含人教版数学八上高分突破训练专项11用截长补短法构造全等三角形综合应用原卷版doc、人教版数学八上高分突破训练专项11用截长补短法构造全等三角形综合应用解析版doc等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
这是一份人教版数学八上高分突破训练专项10 用倍长中线法构造全等三角形综合应用(2份,原卷版+解析版),文件包含人教版数学八上高分突破训练专项10用倍长中线法构造全等三角形综合应用原卷版doc、人教版数学八上高分突破训练专项10用倍长中线法构造全等三角形综合应用解析版doc等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。









