

还剩3页未读,
继续阅读
2024-2025学年重庆市“金太阳联考”高一上学期期中考试数学试题(含答案)
展开这是一份2024-2025学年重庆市“金太阳联考”高一上学期期中考试数学试题(含答案),共6页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
1.命题“∃x<0,|x|>1”的否定为( )
A. ∃x<0,|x|≤1B. ∃x≥0,|x|≤1
C. ∀x<0,|x|≤1D. ∀x≥0,|x|≤1
2.下列结论描述不正确的是( )
A. π∈QB. 2∈{2}C. ⌀⊆ZD. N⊆R
3.下列各组函数f(x)与g(t)是同一个函数的是( )
A. f(x)=|x|,g(t)=( t)2B. f(x)=x2−2xx,g(t)=t−2
C. f(x)=x2−1,g(t)=t4−1t2+1D. f(x)=3x+2,g(t)=2t+3
4.若幂函数f(x)=(m2−3m+1)xm+1的图象关于原点对称,则m=( )
A. 3B. 2C. 1D. 0
5.“a>2”是“a+2a>3”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
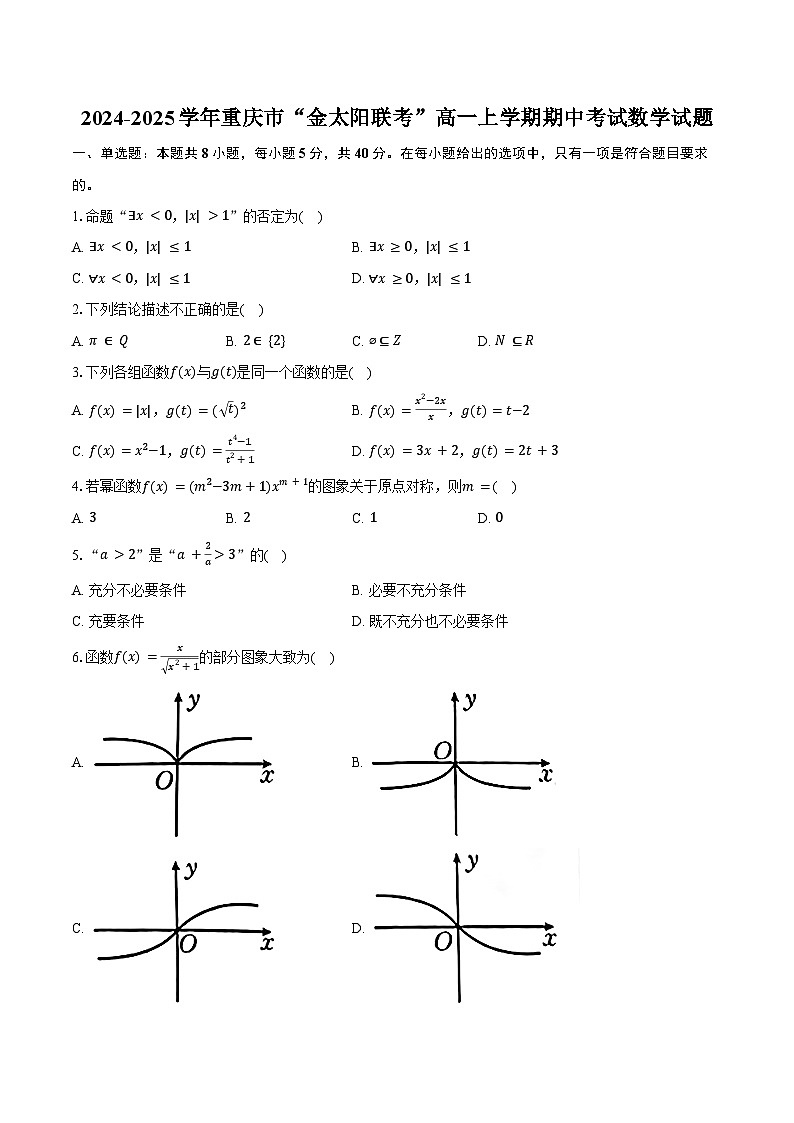
6.函数f(x)=x x2+1的部分图象大致为( )
A. B.
C. D.
7.已知全集U={2,3,4,5,6,7,8},A,B是U的两个子集,且A∩B={5},A∩(∁UB)={2,3,6},则(∁UA)∪B=( )
A. {4,7,8}B. {4,5,7,8}C. {2,3,5,6}D. {3,5,6}
8.已知x>y>0,则2xx−y−8yx+y的最小值为( )
A. 4B. 3C. 2D. 1
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列函数中,既是偶函数,又在(0,+∞)上单调递增的有( )
A. f(x)=x2B. f(x)=−1x
C. f(x)=x4+2x2D. f(x)=−2|x|+1
10.已知a>b>c,d>0,则( )
A. 1a−d<1b−dB. a3>c3C. ad>bdD. b2d>c2d
11.已知函数f(x)满足对任意x∈R,均有f(x)=−2f(x−2),且当x∈[0,2]时,f(x)=x(x−m),则( )
A. m=2
B. f(5)=4
C. 当x∈[4,6]时,f(x)=4(x−4)(x−6)
D. 存在0
12.函数f(x)= 3+xx+1的定义域为 .
13.若−1
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
给出下列两个结论:
①∀x∈[1,3],mx−2m−4<0;
②函数f(x)=x2−(m+1)x−3在[1,2]上单调.
(1)若结论 ①正确,求m的取值范围;
(2)若结论 ① ②都正确,求m的取值范围.
16.(本小题12分)
如图,某花圃基地要建造一面靠墙的两间相同的矩形花室.
(1)若可供建造围墙的材料总长是120米,求每间花室面积的最大值;
(2)若要求每间花室的面积为150平方米,求建造围墙所需的材料总长的最小值.
17.(本小题12分)
已知函数f(x)满足f(x)−2f(−x)=9x+1.
(1)求f(x)的解析式;
(2)若g(x)=x|f(x+a)−a|是奇函数,求a的值.
18.(本小题12分)
已知集合A={x|x2−3x+2<0},B={x|x2−(3a+2)x+2a2+4a<0}.
(1)若a=0,求A∪B;
(2)若A⊆B,求a的取值范围;
(3)若a∈Z,且B中恰有1个整数元素,求a的值.
19.(本小题12分)
定义:f(n)−f(m)n−m为函数f(x)在[m,n]上的平均变化率.
(1)若函数f(x)=x3在[x1,x2]上的平均变化率为3,证明:x1x2<1.
(2)设f(x)=x2+2x,a,b∈(0,1),且f(b)=a2−2a+4.
①证明:a
参考公式:a3−b3=(a−b)(a2+ab+b2).
参考答案
1.C
2.A
3.C
4.D
5.A
6.C
7.B
8.D
9.AC
10.BC
11.ACD
12.−3,−1∪(−1,+∞)
13.(−5,4)
14.(−∞,12)
15.解:(1)由结论 ①正确,得m−2m−4<0,3m−2m−4<0,解得−4
(2)若f(x)在[1,2]上单调递增,则m+12≤1,解得m≤1,
若f(x)在[1,2]上单调递减,则m+12≥2,解得m≥3.
综上所述,当结论 ②正确时,m的取值范围为(−∞,1]∪[3,+∞).
故当结论 ① ②都正确时,m的取值范围为(−4,1]U[3,4).
16.解:设每间花室与墙体垂直的围墙的边长为a米,与墙体平行的围墙的边长为b米.
(1)因为可供建造围墙的材料总长是120米,所以3a+2b≤120,
其中0
因为(120−2b)b3=−23(b2−60b)=−23(b−30)2+600≤600,
当且仅当a=20,b=30时,等号成立,
所以每间花室面积的最大值为600平方米.
(2)因为每间花室的面积为150平方米,所以ab=150,则b=150a.
建造围墙所需的材料总长l=3a+2b=3a+300a≥2 3a⋅300a=60,当且仅当a=10,b=15时,等号成立,
故建造围墙所需的材料总长的最小值为60米.
17.【解答】解:(1)因为f(x)−2f(−x)=9x+1 ①,所以f(−x)−2f(x)=−9x+1 ②.
①+2× ②得−3f(x)=−9x+3,则f(x)=3x−1.
(2)由(1)可知,g(x)=x|f(x+a)−a|=x|3(x+a)−1−a|=x|3x+2a−1|.
因为g(x)是奇函数,所以g(−x)=−g(x),即−x|−3x+2a−1|=−x|3x+2a−1|,则2a−1=0,解得a=12.
18.解:(1)由x2−3x+2<0,得1
若2a
若2a=a+2,即a=2,则B=⌀,不符合A⊆B.
若2a>a+2,即a>2,则B={x|a+2
综上可知,a的取值范围为[0,12].
(3)由(2)知,当a=2时,B=⌀,不合题意;
当a<2时,由B中恰有1个整数元素,得0<2−a≤2,解得0≤a<2.
因为a∈Z,所以a=0或a=1.
经检验知当a=0时,B中恰有1个整数元素1,
当a=1时,B中没有整数元素.
当a>2时,由B中恰有1个整数元素,得0
经检验知当a=3时,B中没有整数元素,
当a=4时,B中恰有1个整数元素7.
综上可知,a=0或a=4.
19.(1)证明:因为f(x)在[x1,x2]上的平均变化率为3,
所以f(x2)−f(x1)x2−x1=x23−x13x2−x1=x22+x1x2+x12=3.
由x1
(2) ①证明:因为f(b)=a2−2a+4,
所以f(b)−f(a)=a2−2a+4−a2−2a=−2(a+1a−2),
又0
f(b)−f(a)b−a=b2+2b−a2−2ab−a=a+b−2ab,
因为a,b∈(0,1),所以a+b<2,0
又f(b)−f(a)<0,所以b−a>0,即a
即f(x3)>f(x4),所以f(x)在(0,1)上单调递减,
由a
相关试卷
2024-2025学年广东省“金太阳联考”高二(上)期中考试数学试题(含答案):
这是一份2024-2025学年广东省“金太阳联考”高二(上)期中考试数学试题(含答案),共8页。试卷主要包含了单选题,多选题,填空题等内容,欢迎下载使用。
2024-2025学年河南省“金太阳联考”高一年级上学期期中考试数学试题(含答案):
这是一份2024-2025学年河南省“金太阳联考”高一年级上学期期中考试数学试题(含答案),共7页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
重庆市部分学校2024-2025学年高一上学期期中考试数学试题:
这是一份重庆市部分学校2024-2025学年高一上学期期中考试数学试题,文件包含重庆市部分学校2024-2025学年度高2027届高一上学期期中考试数学试题pdf、数学答案pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。








