2024-2025学年北京市东城区第五中学高一上学期期中考试数学试题（含答案）

这是一份2024-2025学年北京市东城区第五中学高一上学期期中考试数学试题（含答案），共8页。试卷主要包含了单选题等内容，欢迎下载使用。
1.已知集合A=xx≥0,B=xx≤3，则A∩∁RB=( )
A. 0,+∞B. 0,+∞C. −∞,3D. 3,+∞
2.命题“∀x∈Z,|x|>0”的否定是( )
A. ∀x∉Z,|x|>0B. ∀x∈Z,|x|≤0C. ∃x∉Z,|x|>0D. ∃x∈Z,|x|≤0
3.已知a>b,c>d，则下面不等式一定成立的是( )
A. a+d>b+cB. a+db−cD. a−d1”是不等式x+1x−1>0成立的( )．
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
5.已知定义在R上的偶函数fx在−∞,0上是增函数，且f−1=0，则使fx>0的x的取值范围是( )
A. −1,0B. 0,1
C. −1,1D. −∞,−1∪1,+∞
6.已知函数f(x)=(a−3)x+5,x≤12ax,x>1是(−∞,+∞)上的减函数，则a的取值范围是( )
A. (0,3)B. (0,3]C. (0,2)D. (0,2]
7.如图所示，点P在边长为1的正方形的边上运动，设M是CD边的中点，则当点P沿着A−B−C−M运动时，以点P经过的路程x为自变量，三角形APM的面积函数y的图象形状大致是( )
A. B.
C. D.
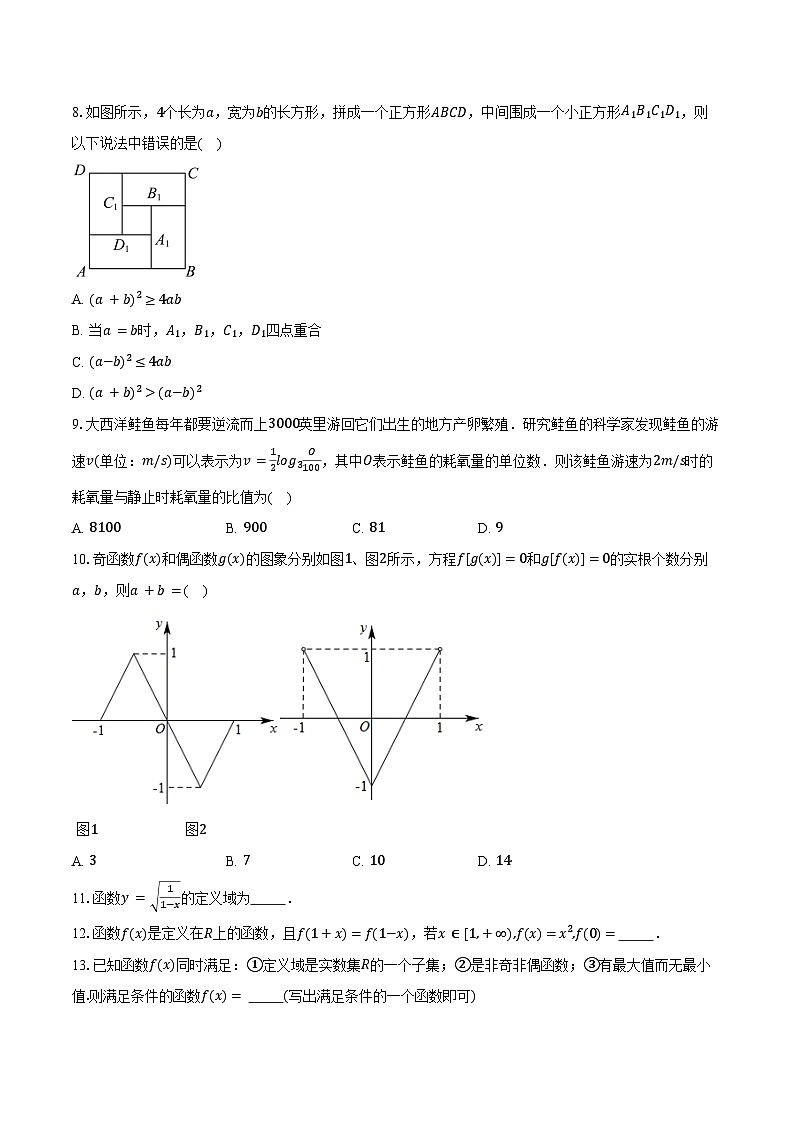
8.如图所示，4个长为a，宽为b的长方形，拼成一个正方形ABCD，中间围成一个小正方形A1B1C1D1，则以下说法中错误的是( )
A. (a+b)2≥4ab
B. 当a=b时，A1，B1，C1，D1四点重合
C. (a−b)2≤4ab
D. (a+b)2>(a−b)2
9.大西洋鲑鱼每年都要逆流而上3000英里游回它们出生的地方产卵繁殖．研究鲑鱼的科学家发现鲑鱼的游速v(单位：m/s)可以表示为v=12lg3O100，其中O表示鲑鱼的耗氧量的单位数．则该鲑鱼游速为2m/s时的耗氧量与静止时耗氧量的比值为( )
A. 8100B. 900C. 81D. 9
10.奇函数fx和偶函数gx的图象分别如图1、图2所示，方程fgx=0和gfx=0的实根个数分别a，b，则a+b=( )
图1 图2
A. 3B. 7C. 10D. 14
11.函数y= 11−x的定义域为 ．
12.函数fx是定义在R上的函数，且f1+x=f1−x，若x∈1,+∞,fx=x2,f0= ．
13.已知函数fx同时满足：①定义域是实数集R的一个子集；②是非奇非偶函数；③有最大值而无最小值.则满足条件的函数fx= (写出满足条件的一个函数即可)
14.农业技术员进行某种作物的种植密度试验，把一块试验田划分为8块面积相等的区域(除了种植密度，其它影响作物生长的因素都保持一致)，种植密度和单株产量统计如下：
根据上表所提供信息，第 号区域的总产量最大，该区域种植密度为 株/m2．
15.对于函数fx=2x−12x+1，下列说法正确的是 .(写出所有正确命题的序号)
①函数fx为奇函数； ②函数fx的值域为−23,23；
③函数在定义域上为增函数； ④对于∀a∈R，均有fa+1>fa−1．
16.计算：
(1) 614+33813+3125；
(2)lg43⋅lg92−lg1232；
(3)2723×3lg32× 3+10÷1681−34．
17.已知关于x的不等式(ax−1)(x−2)>2的解集为A，且3∉A．
(I)求实数a的取值范围；
(II)求集合A．
18.函数fx=4x+2x+a，gx=2x．
(1)若fx过点0,3，求a的值；
(2)在(1)的条件下，若x∈0,1，求fx的最大值；
(3)若y=fx图象恒在y=gx图象的上方，求实数a的取值范围．
19.已知函数fx=ax2+bx，且f1=2，f2=52．
(1)确定函数fx的解析式，并判断奇偶性；
(2)用定义证明函数fx在区间−∞,−1上单调递增；
(3)求满足f1+2t2−f3+t20⇔ax2−(2a+1)x>0
当a=0时，集合A=x|x