2024年陕西省榆林市高新区中考二模数学试题(含答案)

这是一份2024年陕西省榆林市高新区中考二模数学试题(含答案)，共13页。试卷主要包含了本试卷分为第一部分，领到试卷和答题卡后，请用0等内容，欢迎下载使用。
注意事项：
1.本试卷分为第一部分（选择题）和第二部分（非选择题）。全卷共6页，总分120分。考试时间120分钟。
2.领到试卷和答题卡后，请用0.5毫米黑色墨水签字笔，分别在试卷和答题卡上填写姓名和准考证号，同时用2B铅笔在答题卡上填涂对应的试卷类型信息点（A或B）。
3.请在答题卡上各题的指定区域内作答，否则作答无效。
4.作图时，先用铅笔作图，再用规定签字笔描黑。
5.考试结束，本试卷和答题卡一并交回。
第一部分（选择题 共21分）
一、选择题（共7小题，每小题3分.计21分.每小题只有一个选项是符合题意的）
1.的相反数是
A.B. C.D.
2.下列几何体中，左视图是矩形的是
A. B. C. D.
3.如图，已知直线，直角三角板的直角顶点在直线a上，若，则的度数为
A.60°B.40°C.30°D.20°
4下列运算正确的是
A.B.C.D.
5.在平面直角坐标系中，把直线（k为常数且）向右平移2个单位长度，平移后的直线经过点，则k的值为
A.1B.2C.3D.4
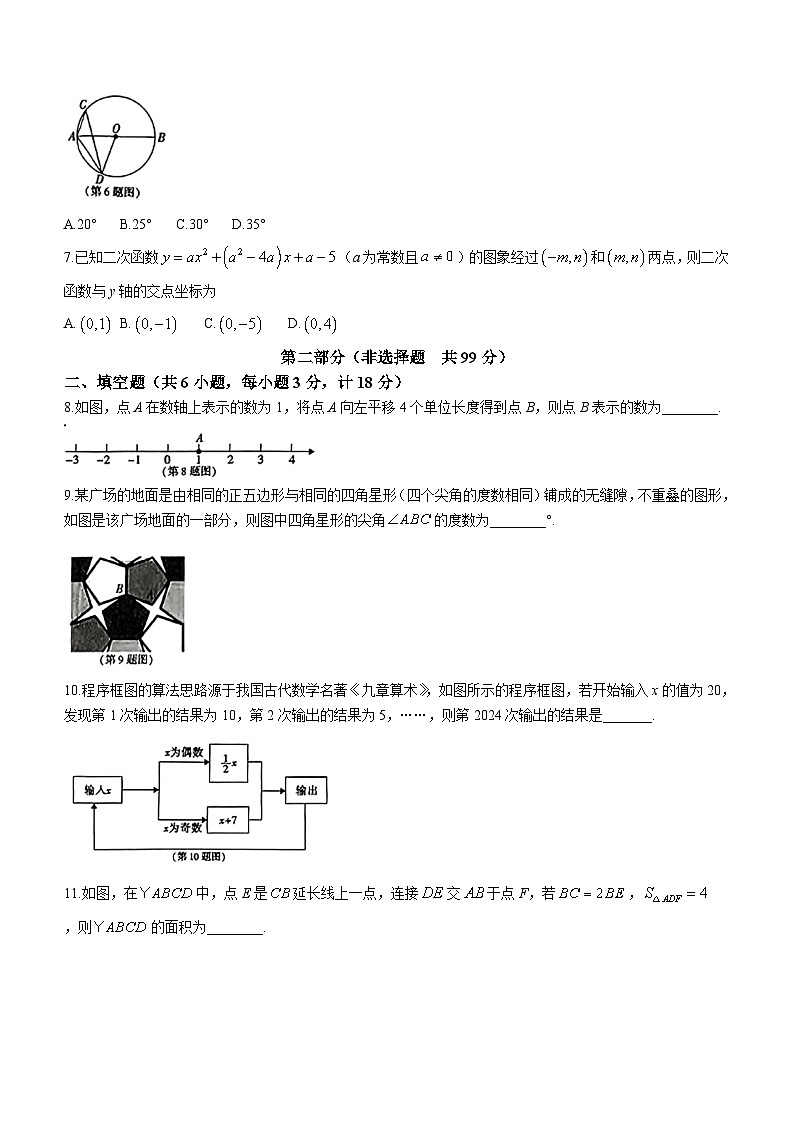
6.如图，是的直径，是的弦，交于点D，连接、，若，则的度数为
A.20°B.25°C.30°D.35°
7.已知二次函数（a为常数且）的图象经过和两点，则二次函数与y轴的交点坐标为
A.B.C.D.
第二部分（非选择题 共99分）
二、填空题（共6小题，每小题3分，计18分）
8.如图，点A在数轴上表示的数为1，将点A向左平移4个单位长度得到点B，则点B表示的数为________.
9.某广场的地面是由相同的正五边形与相同的四角星形（四个尖角的度数相同）铺成的无缝隙，不重叠的图形，如图是该广场地面的一部分，则图中四角星形的尖角的度数为________°.
10.程序框图的算法思路源于我国古代数学名著《九章算术》，如图所示的程序框图，若开始输入x的值为20，发现第1次输出的结果为10，第2次输出的结果为5，……，则第2024次输出的结果是_______.
11.如图，在中，点E是延长线上一点，连接交于点F，若，
，则的面积为________.
12.若反比例函数（k为常数且）与一次函数的一个交点的坐标为.则k的值为________.
13.如图，在矩形中，，，点E是对角线上的一个动点，连接，点F在线段上，连接、，若，则的最小值为________.
三、解答题（共14小题.计81分.解答应写出过程）
14.（本题满分4分）
计算：.
15.（本题满分4分）
解不等式组：
16.（本题满分4分）
化简：.
17.（本题满分4分）
如图，在中，利用尺规作图法求作，使得与的交点C到点O的距离最短.（不写作法，保留作图痕迹）
18.（本题满分4分）
如图，在四边形中，，连接、，且，求证：四边形是矩形.
19.（本题满分5分）
某商场因换季清仓，对某件标价为200元的服装进行打折销售，若按标价打8折，再降价10元销售，仍可获利25%，求这件服装的进价.
20.（本题满分5分）
求证：对任意整数n，整式的值都能被10整除.
21.（本题满分5分）
甲、乙两人玩转转盘游戏，如图所示的转盘被平均分成三个面积相等的扇形区域.额色分别为红、黄、蓝，转动转盘时，指针指向的颜色，即为转出的颜色（如果指针指在两区域的分界线上，则重转一次），甲转动转盘两次，乙不看甲转出的结果猜测两次转出的颜色相同.若乙的猜测与甲转出的结果相同，则乙获胜；若乙的猜测与甲转出的结果不同，则甲获胜。
（1）甲转出的结果为“两次转出的颜色中没有红色”是_________事件；（填“确定”或“随机”）
（2）请用列表或画树状图的方法求乙获胜的概率
22.（本题满分6分）
某数学兴趣小组测量一栋居民楼高度的活动报告如下：
请你根据该兴趣小组的测量结果求出该居民楼的高度.
23.（本题满分7分）
世界水日为每年的3月22日，宗旨是唤起公众的节水意识，加强水资源保护。某 节约用水，采取阶梯分段收费标准，已知用户每月用水量不超过15吨时，水费为a元/吨，每月应交水费y（元）与用水量x（吨）之间的函数关系如图所示.
（1）填空：__________；
（2）当用水量x超过15吨时，求y与x之间的函数表达式；
（3）若某用户3月份交水费45元，求该用户3月份的用水量.
24.（本题满分7分）
二十四节气是中华民族悠久历史文化的重要组成部分，被国际气象学界誉为“中国的第五大发明”．为了了解学生掌握中华传统节气知识的情况，增强学生民族自豪感，某校在春分这天举行了以“春趣盎然，莫负春分好时光”为主题的知识竞赛活动（全校学生均参加），并从中随机抽取了50名学生的竞赛成绩（分数为整数，满分10分），将调查结果绘制成如下不完整的统计图：
根据以上信息，解答下列问题：
（1）请补全条形统计图；
（2）求所抽取学生此次竞赛成绩的平均数、中位数与众数；
（3）已知该校共有1500名学生，估计此次竞赛成绩不低于9分的学生人数。
25.（本题满分8分）
如图，在中，以为直径的交于点D，点E是的中点，连接交于点F，且.
（1）求证：是的切线；
（2）若，，求的长.
26.（本题满分8分）
如图，已知抛物线与y轴交于点C，与x轴交于，两点.
（1）求抛物线的函数表达式；
（2）若点D是第二象限抛物线上的动点，轴，交直线于点E，点G在x轴上，点F在坐标平面内.是否存在点D，使以D，E，F，G为顶点的四边形是正方形?若存在，求点D的坐标；若不存在，请说明理由.
27.（本题满分10分）
【问题提出】
（1）如图1，在中，点D、E分别在、上，连接，且，若，，则的长为_______；
【问题探究】
（2）如图2，在和中，点B、C、D在同一条直线上，，，判断与的数量关系，并说明理由；
【问题解决】
（3）如图3，五边形是某植物园的平面图，C、D分别是植物园的入口和出口（可看作点），和是进出植物园的两条主路，该植物园为举行春季花展，现要在出入口C、D之间进行花墙装饰工作.已知，，，，，求装饰的花墙的长度.（结果保留根号）
数学试卷参考答案及评分标准
一、选择题（共7小题，每小题3分，计21分.每小题只有一个选项是符合题意的）
1.B 2.A 3.C 4.D 5.C 6.A 7.B
二、填空题（共6小题，每小题3分，计18分）
8. 9.18 10.6 11.12 12.5
13.2【解析】由题意可得，，则，易得.取的中点G，连接、，可得，.在中，，当A、F、G三点共线时，最小，此时，即，的最小值为2.
三、解答题（共14小题，计81分.解答应写出过程）
14.解：原式
.
15.解：解不等式，得，…
解不等式，得，
不等式组的解集为.
16.解：原式
.
17.解：如图所示，即为所求.
注；①答案中线条为实线或虚线均不扣分；②没有写出结论不扣分.
18.证明：
，和是直角三角形.
在和中，，，
（HL），
，
四边形是平行四边形.
四边形是矩形.
19.解：设这件服装的进价为x元，
，
解得，
答：这件服装的进价为120元.
20.证明：原式
.
n为整数，
能被10整除，
对任意整数n，原式的值都能被10整除.
21.解：（l）随机.
（2）画树状图如下：
由图可知共有9种等可能的结果，其中两次转出的颜色相同的结果有3种，
乙获胜的概率为.
注：①在（2）中如果求出的概率正确，但没有列表格或画树状图扣2分；求出概率正确，若列表或画树状图后没有就结果作出说明不扣分；②在（2）中若运用枚举法直接列举出9种等可能结果，只要结果正确，不扣分.
22.解：延长交的延长线于点G，过点C作于点H.
则四边形是矩形，，.
由，坡度，易得，，
（m）.
，
（m）.
在中，，即
，则，
（m）
该居民楼的高度为34.5m.
注：没有单位，没有答语不扣分.
23.解：（1）2.
（2）当用水量x超过15吨时，设y与x之间的函数表达式为，
将,代入，得
解得，
解付1b=-15.
当用水量x超过15吨时，y与x之间的函数表达式为.
（3）由可知该用户3月份用水量超过15吨，
令，
解得，
该用户3月份的用水量为20吨.
24.解：（1）补全条形统计图如下：
（2）（分），
所抽取学生此次竞赛成绩的平均数是7.66分.
按从小到大排列，排在最中间的两个数都是8分，
中位数是8分
出现次数最多的是8，众数是8分.
（3）（人），
估计此次竞赛成绩不低于9分的学生有510人.
注：①（2）中平均数没有计算过程扣1分：②（3）中没有计算过程扣1分，没有单位，没有答语不扣分.
25.（1）证明：连接.
是的直径，
，则，
点E是的中点，
，则.
，
，
，即，
是的切线.
（2）解：，，
.
设，则，
，即，
解得（负值舍去），则，.
，
，
.
26.解：（1）将，代入中，
得
解得
抛物线的函数表达式为.
（2），，
设直线的函数表达式为：，
将代入得：，
，
直线的函数表达式为.
设，分两种情况：
当为边时，如图1，四边形是正方形（点G、F可互换位置）.
则点E的坐标为，
，即
解得（舍）或，
点D的坐标为.
②当为对角线时，如图2，连接，过点D作轴于点H，易得，
则
点E的坐标为.
点E在直线上，
，
解得或2（舍），
点D的坐标为.
综上可得：存在点D，使得以D，E，F，G为顶点的四边形是正方形，点D的坐标为或.
27.解：（1）5.
（2）.理由如下：
，点B，C、D在同一条直线上，
.
在和中，，，，
（ASA），
.
（3）过点D作交的延长线于点F，过点F作交的延长线于点M，交的延长线于点N，延长交于点G.
易得四边形、四边形和四边形是矩形，
，，，，.
在中，，，
，，
，
，
.
在和中，，，，
，
，.
设，则，
在中，，，
，
.
，
，即，
解得，
，
故装饰的花墙的长度为m.
活动目的
测量居民楼的高度
测量工具
皮尺、测角仪
测量示意图及说明
说明：测量仪、居民棱。点B、E在水平地面上。A、B、C、D、E、F均在同一平面内
测量过程及数据
测量小组在距离居民楼（）处的斜坡上的点D处放置测角仪，测得居民楼楼顶A的仰角为37°，斜坡的坡度，，
参考数据
，，
备注
测量过程注意安全