湖北省2023年春季重点高中自主招生考试优录测试八校联考中考模拟数学试题一（含答案）

这是一份湖北省2023年春季重点高中自主招生考试优录测试八校联考中考模拟数学试题一（含答案），文件包含优录数学试题一参考答案docx、2023年春季重点高中自主招生考试优录测试数学试题一pdf等2份试卷配套教学资源，其中试卷共15页， 欢迎下载使用。
参考答案
一、选择题（每小题3分，共24分）
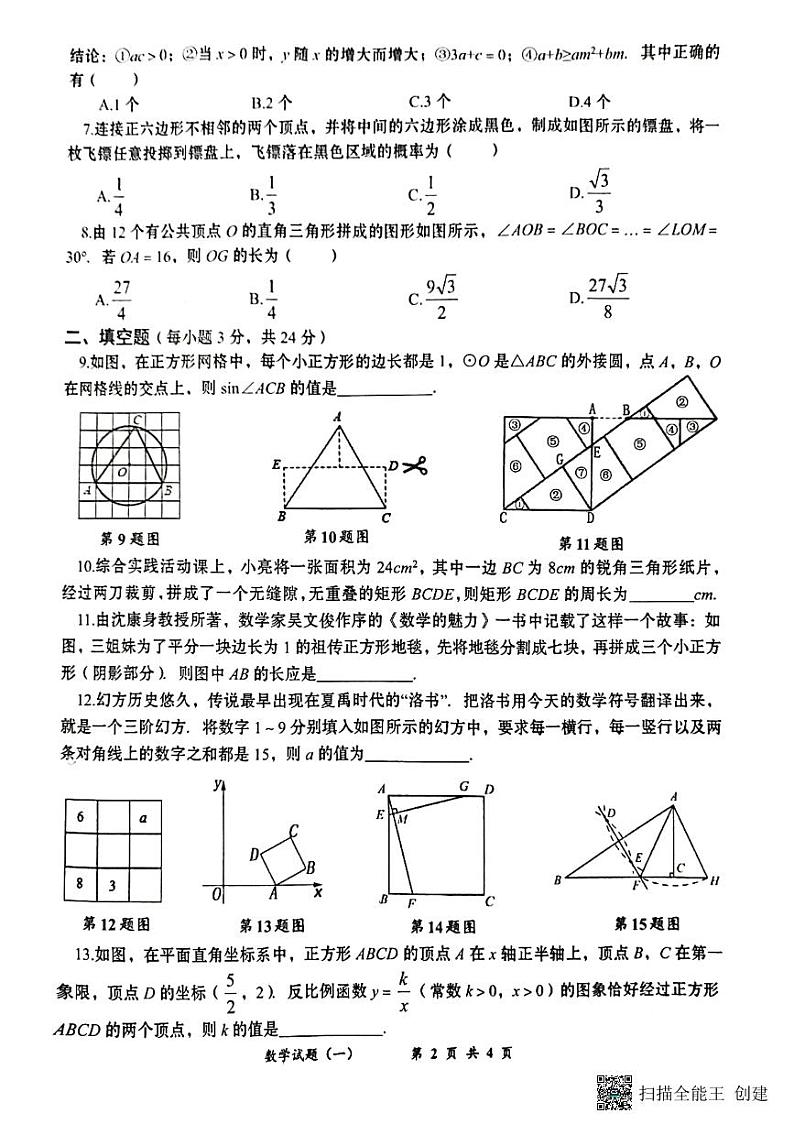
1．D．
解析：混合之后糖的含量：．
2．A．
解析：如图，过点C作于F，过点B作于E，
∵长方形纸片分别沿AB，AC折叠，点M，N恰好重合于点P，
∴，∴，
∴，，，
∴cm2，∴．
3．D．
解析：设DE交AC于T，过点E作EH⊥CD于H．
∵∠BAC＝90°，BD＝DC，∴AD＝DB＝DC，
∴∠B＝∠DAB，
∵∠B＝∠ADE，∴∠DAB＝∠ADE，∴AB∥DE，
∴∠DTC＝∠BAC＝90°，
∵DT∥AB，BD＝DC，∴AT＝TC，∴EA＝EC＝ED，
∴∠EDC＝∠ECD，
∵EH⊥CD，∴CH＝DH，∵DE∥AB，∴∠EDC＝∠B，
∴∠ECD＝∠B，
∴cs∠ECH＝csB＝，∴＝，∴＝＝2．
4．B．
解析：如图，C1运动的路径是以B为圆心，为半径，圆心角为120°的弧上运动，故线段CC1扫过的区域是一个圆心角为120°的扇形＋一个以为边长的等边三角形，
故S＝．
5．C．
解析：∵顾客从一批大小不一的鸡蛋中选购了部分大小均匀的鸡蛋，∴＜s2，的大小关系不明确.
6．B．
解析：把点A（﹣1，0），B（3，0）代入二次函数y＝ax2+bx+c，可得二次函数的解析式为：y＝ax2﹣2ax﹣3a，∵该函数开口方向向下，∴a＜0，∴b＝﹣2a＞0，c＝﹣3a＞0，∴ac＜0，3a+c＝0，①错误，③正确；∵对称轴为直线：x＝﹣＝1，∴x＜1时，y随x的增大而增大，x＞1时，y随x的增大而减小；②错误；∴当x＝1时，函数取得最大值，即对于任意的m，有a+b+c≥am2+bm+c，∴a+b≥am2+bm，故④正确．综上，正确的个数有2个．
7．B．
解析：如图所示，令S△ABC＝a，则S阴影＝6a，S正六边形＝18a，
∴将一枚飞镖任意投掷到镖盘上，飞镖落在黑色区域的概率为．
8．A．
解析：由图可知，∠ABO＝∠BCO＝…＝∠LMO＝90°，
∵∠AOB＝∠BOC＝…＝∠LOM＝30°，∴∠A＝∠OBC＝∠OCD＝…＝∠OLM＝60°，
∴AB＝OA，OB＝AB＝OA，同理可得，OC＝OB＝OA，
OD＝OC＝OA，…，OG＝OF＝OA＝×16＝．
二、填空题（每小题3分，共24分）
9．．
解析：如图，连接AO并延长交⊙O于D，由圆周角定理得：
∠ACB＝∠ADB，由勾股定理得：AD＝，
∴sin∠ACB＝sin∠ADB＝＝.
10．22．
解析：延长AT交BC于点P，∵AP⊥BC，∴•BC•AP＝24，
∴×8×AP＝24，∴AP＝6cm，由题意，AT＝PT＝3cm，
∴BE＝CD＝PT＝3cm，∵DE＝BC＝8cm，
∴矩形BCDE的周长为8+8+3+3＝22cm．
11．﹣1．
解析：CD＝1，DG＝，则求得CG＝，根据△CDG∽△DEG，可求得DE＝，
∴AE＝1﹣，∴AB＝AE＝﹣1．
12．2．
解析：幻方右下角的数字为15﹣8﹣3＝4，幻方第二行中间的数字为15﹣6﹣4＝5．依题意得：8+5+a＝15，解得：a＝2．
13．5或22.5
解析：作DM⊥x轴于M，BN⊥x轴于N，过C点作x轴的平行线，交DM于E，交BN于F，正方形ABCD中，∠BAD＝90°，∴∠DAM+∠BAN＝90°，
∵∠ADM+∠DAM＝90°，∴∠ADM＝∠BAN，
在△ADM和△BAN中，，
∴△ADM≌△BAN（AAS），∴AM＝BN，DM＝AN，
∵顶点D的坐标（，2）．∴OM＝，DM＝2，
同理：△ADM≌△DCE，∴AM＝DE，CE＝DM，
∴AM＝BN＝DE，DM＝AN＝CE＝2，设AM＝BN＝DE＝m，∴ON＝+m+2＝4.5+m，∴B（4.5+m，m），C（4.5，2+m），当反比例函数y＝（常数k＞0，x＞0）的图象经过点B、D时，则k＝×2＝5；当反比例函数y＝（常数k＞0，x＞0）的图象经过点B、C时，则k＝（4.5+m）•m＝4.5•（2+m），解得m＝3（负数舍去），∴k＝4.5×（2+3）＝22.5．
14．．
解析：∵在正方形ABCD中，AF⊥EG，∴∠AGE+∠GAM =90°，∠FAB+∠GAM=90°，
∴∠FAB =∠AGE，又∵∠ABF=∠GAE=90°，∴，∴，即，∴BF=．
15．6．
解析：由作图可得DF垂直平分线段AB，∴，∵以点A为圆心，AF为半径画弧，交BC延长线于点H，∴，∴，∵，∴，
∴△AFH的周长．
16．2±2或4或2．
解析：如图，当C，D在AB的同侧时，过点A作AE⊥CD于E．在Rt△AEB中，∠AEB＝90°，AB＝4，∠ABE＝30°，∴AE＝AB＝2，∵AD＝AC＝2，∴DE＝＝2，EC＝＝2，∴DE＝EC＝AE，∴△ADC是等腰直角三角形，∴CD＝4，
当C，D在AB的异侧时，过C′作C′H⊥CD于H，∵△BCC′是等边三角形，BC＝BE﹣EC＝2﹣2，
∴CH＝BH＝﹣1，C′H＝CH＝3﹣，在Rt△DC′H中，
DC′＝＝＝2，
∵△DBD′是等边三角形，∴DD′＝2+2，
∴CD的长为2±2或4或2．
三、解答题（共72分）
17．（10分）解：（1）∵点A在正比例函数y＝x的图象上，AB⊥y轴，OB＝4，
∴点B的坐标为（0，4），点A的纵坐标是4，代入y＝x，得x＝8，∴A（8，4），
∵点A在反比例函数y＝（x＞0）的图象上，∴k＝4×8＝32，
∵点C在线段AB上，且AC＝OC，∴设点C（c，4）．
∵OC＝＝，AC＝AB﹣BC＝8﹣c，
∴＝8﹣c，解得：c＝3，∴点C（3，4），
∴BC＝3，∴k＝32，BC＝3；分
（2）如图，设点P（0，p），
∵点P为B点上方y轴上一点，∴OP＝p，BP＝p﹣4，
∵A（8，4），C（3，4），∴AC＝8﹣3＝5，BC＝3，
∵△POC与△PAC的面积相等，
∴×3p＝×5（p﹣4），解得：p＝10，
∴P（0，10）． 分
18．（12分）解：（1）∵四边形ABCD和四边形AEGF都是正方形，∴AD＝AB，AF＝AE，∠DAE＝∠BAF＝90°，∴△DAE≌△BAF（SAS），∴DE＝BF，∠ADE＝∠ABF，∵∠ABF+∠AFB＝90°，∴∠ADE+∠AFB＝90°，∵在Rt△BAF中，M是BF的中点，∴AM＝FM＝BM＝BF，∴DE＝2AM．∵AM＝FM，∴∠AFB＝∠MAF，又∵∠ADE+∠AFB＝90°，∴∠ADE+∠MAF＝90°，∴∠AND＝180°﹣（∠ADE+∠MAF）＝90°，即AN⊥DN；故DE＝2AM，DE⊥AM． 分
（2）仍然成立，证明如下：延长AM至点H，使得AM＝MH，连接FH，
∵M是BF的中点，∴BM＝FM，又∵∠AMB＝∠HMF，∴△AMB≌△HMF（SAS），∴AB＝HF，∠ABM＝∠HFM，∴AB∥HF，∴∠HFG＝∠AGF，∵四边形ABCD和四边形AEGF是正方形，∴∠DAB＝∠AFG＝90°，AE＝AF，AD＝AB＝FH，∠EAG＝∠AGF，∴∠EAD＝∠EAG+∠DAB＝∠AFG+∠AGF＝∠AFG+∠HFG＝∠AFH，∴△EAD≌△AFH（SAS），∴DE＝AH，又∵AM＝MH，∴DE＝AM+MH＝2AM，
∵△EAD≌△AFH，∴∠ADE＝∠FHA，
∵△AMB≌△HMF，∴∠FHA＝∠BAM，
∴∠ADE＝∠BAM，
又∵∠BAM+∠DAM＝∠DAB＝90°，
∴∠ADE+∠DAM＝90°，
∴∠AND＝180°﹣（∠ADE+∠DAM）＝90°，
即AN⊥DN．故线段DE与AM之间的数量关系
是DE＝2AM．线段DE与AM之间的位置关系
是DE⊥AM． 分
19．（12分）（1）解：，，，，是等边三角形， 是的中点，，在中，，，． 分
（2）证明：连接，，，，， ，，，又，，是等边三角形，
，，
又，， ． 分
（3）存在这样的． 分
20．（12分）解：（1）①∵点A是劣弧的中点，∴，∴，∵四边形ABCD是平行四边形，∴平行四边形ABCD是菱形；分
②连接AO，交BD于点E，连接OD，∵点A是劣弧的中点，OA为半径，
∴，OA平分BD，∴，∵平行四边形ABCD是菱形，∴E为两对角线的交点，在中，
,∴，∴；分
（2）①如图，当CD与相切时，连接DO并延长，交AB于点F，
∵CD与相切，∴，∴，
∵四边形ABCD是平行四边形，
∴，∴，在中，
，在中，
，∴，
解得，∴，∴；
如图，当BC与相切时，连接BO并延长，
交AD于点G，同理可得，，所以,
综上所述，AB长为或；分
②过点AH作于点H，由（2）得： 根据等面积法可得，解得，在中，，∴，∴．分
21．（12分）解：（1）设四月和五月这两个月中，该景区游客人数的月平均增长率为，
由题意，得 解这个方程，得（舍去）．
答：四月和五月这两个月中，该景区游客人数平均每月增长20%．分
（2）①由题意，得
（万元）
答：景区六月份的门票总收入为798万元． 分
②设丙种门票价格降低元，景区六月份的门票总收人为万元，由题意，得
化简，得，
，∴当时，取最大值，为817.6万元．
答：当丙种门票价格降低24元时，景区六月份的门票总收人有最大值，为817.6万元． 分
22．（14分）解：（1）由点A的坐标知，OA＝2，∵OC＝2OA＝4，故点C的坐标为（0，4），将点A，B，C的坐标代入抛物线表达式得：，解得，故抛物线的表达式为y＝﹣x+x+4；将点B，C的坐标代入一次函数表达式得：，解得，故直线BC的表达式为y＝﹣x+4；分
（2）∵点A，B关于抛物线的对称轴对称，∴设抛物线的对称轴交BC于点F，如图1，则点F为所求点，此时，当FA+FC的值最小，理由如下：
由函数的对称性知，AF＝BF，则AF+FC＝BF+FC＝BC为最小，当x＝1时，y＝﹣x+4＝3，故点F（1，3），由点B、C的坐标知，OB＝OC＝4，则BC＝BO＝4，即点F的坐标为（1，3），FA+FC的最小值为4；分
（3）存在，理由：设点P的坐标为（m，﹣m2+m+4），点Q的坐标为（t，﹣t+4），
①当点Q在点P的左侧时，如图2，过点P，Q分别作x轴的垂线，垂足分别为N，M，
由题意得：∠PEQ＝90°，∴∠PEN+∠QEM＝90°，∵∠EQM+∠QEM＝90°，∴∠PEN＝∠EQM，∴∠QME＝∠ENP＝90°，∴△QME∽△ENP，∴＝tan∠EQP＝tan∠OCA＝＝＝，则PN＝﹣m2+m+4，ME＝1﹣t，EN＝m﹣1，QM＝﹣t+4，∴＝＝，解得m＝±（舍去负值），当m＝时，﹣m2+m+4＝，故点P的坐标为（，）． 分
②当点Q在点P的右侧时，如图3，分别过点P，Q作抛物线对称轴的垂线，垂足分别为N、M，则MQ＝t﹣1，ME＝t﹣4，NE＝﹣m2+m+4、PN＝m﹣1，同理可得：△QME∽△ENP，∴＝tan∠PQE＝2，即，解得m＝（舍去负值），故m＝，故点P的坐标为（，），
综上所述，点P的坐标为（，）或（，）． 分