【高中物理】一轮复习：基本概念、规律、模型及结论回顾总结（2025版）-学案

这是一份【高中物理】一轮复习：基本概念、规律、模型及结论回顾总结（2025版）-学案，共48页。学案主要包含了十种力的特点，力的合成，匀变速直线运动的规律，平抛运动规律，匀速圆周运动的规律，万有引力与天体运动，功与能，动量等内容，欢迎下载使用。
使用说明：高考在即，不要求考生死记硬背，只需结合下文口诀，将高中物理知识回顾下，不清楚的地方一定要查书巩固。
一、十种力的特点
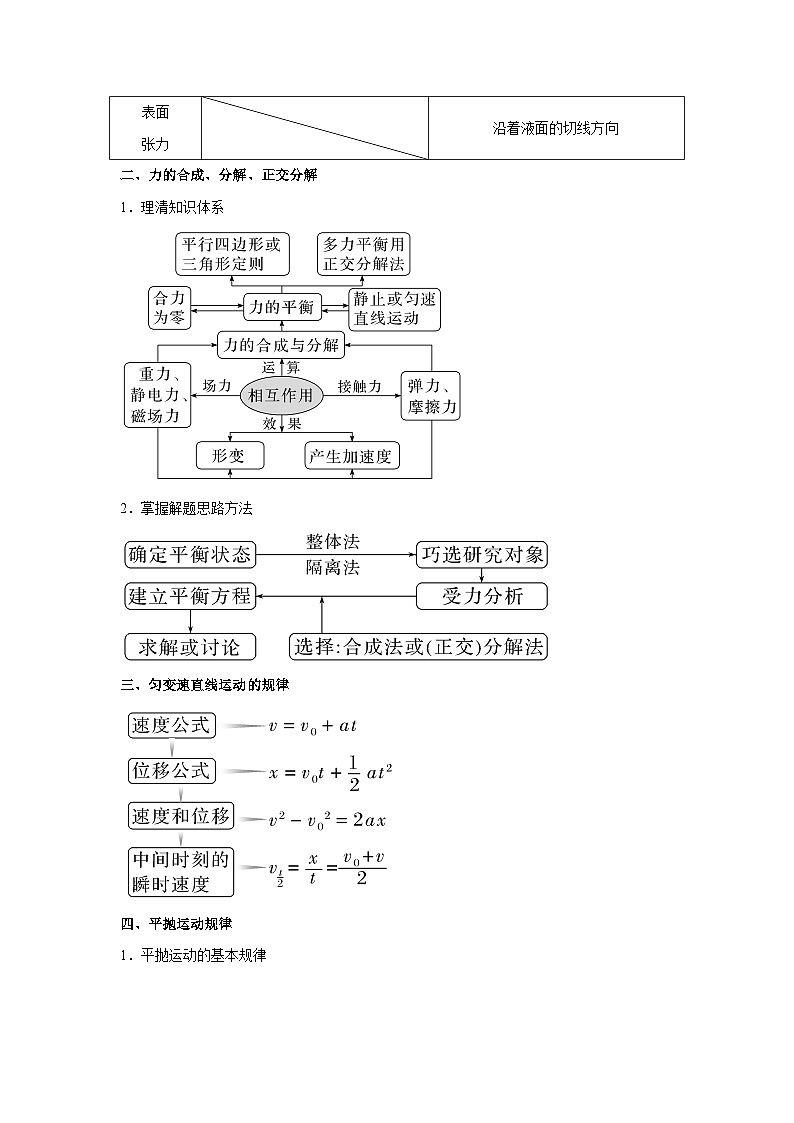
二、力的合成、分解、正交分解
1．理清知识体系
2．掌握解题思路方法
三、匀变速直线运动的规律
四、平抛运动规律
1．平抛运动的基本规律
2．与斜面相关联的平抛运动
五、匀速圆周运动的规律
六、万有引力与天体运动
1．解决天体(卫星)运动问题的基本思路
(1)天体运动的向心力来源于天体之间的万有引力，即
Geq \f(Mm,r2)＝man＝meq \f(v2,r)＝mω2r＝meq \f(4π2r,T2)
(2)在中心天体表面或附近运动时，万有引力近似等于重力，即Geq \f(Mm,R2)＝mg(g表示天体表面的重力加速度)。
2．天体质量和密度的计算
(1)利用天体表面的重力加速度g和天体半径R。
由于Geq \f(Mm,R2)＝mg，故天体质量M＝eq \f(gR2,G)，天体密度ρ＝eq \f(M,V)＝eq \f(M,\f(4,3)πR3)＝eq \f(3g,4πGR)。
(2)通过观察卫星绕天体做匀速圆周运动的周期T和轨道半径r。
①由万有引力等于向心力，即Geq \f(Mm,r2)＝meq \f(4π2,T2)r，得出中心天体质量M＝eq \f(4π2r3,GT2)；
②若已知天体半径R，则天体的平均密度ρ＝eq \f(M,V)＝eq \f(M,\f(4,3)πR3)＝eq \f(3πr3,GT2R3)；
③若天体的卫星在天体表面附近环绕天体运动，可认为其轨道半径r等于天体半径R，则天体密度ρ＝eq \f(3π,GT2)。可见，只要测出卫星环绕天体表面运动的周期T，就可估算出中心天体的密度。
3．第一宇宙速度的理解与计算
(1)第一宇宙速度v1＝7.9 km/s，既是发射卫星的最小发射速度，也是卫星绕地球运行的最大环绕速度。
(2)第一宇宙速度的求法
①eq \f(GMm,R2)＝meq \f(veq \\al(2,1),R)，所以v1＝eq \r(\f(GM,R))。
②mg＝eq \f(mveq \\al(2,1),R)，所以v1＝eq \r(gR)。
4．卫星运行参数的分析与计算
5．卫星(航天器)的变轨问题
(1)轨道的渐变
做匀速圆周运动的卫星的轨道半径发生缓慢变化，由于半径变化缓慢，卫星每一周的运动仍可以看做是匀速圆周运动。解决此类问题，首先要判断这种变轨是离心还是向心，即轨道半径r是增大还是减小，然后再判断卫星的其他相关物理量如何变化。
(2)轨道的突变
由于技术上的需要，有时要在适当的位置短时间启动飞行器上的发动机，使飞行器轨道发生突变，使其进入预定的轨道。
①当卫星的速度突然增加时，Geq \f(Mm,r2)＜meq \f(v2,r)，即万有引力不足以提供向心力，卫星将做离心运动，脱离原来的圆轨道，轨道半径变大，当卫星进入新的轨道稳定运行时由v＝eq \r(\f(GM,r))可知其运行速度比原轨道时减小。
②当卫星的速度突然减小时，Geq \f(Mm,r2)＞meq \f(v2,r)，即万有引力大于所需要的向心力，卫星将做近心运动，脱离原来的圆轨道，轨道半径变小，当卫星进入新的轨道稳定运行时由v＝eq \r(\f(GM,r))可知其运行速度比原轨道时增大；卫星的发射和回收就是利用这一原理。
不论是轨道的渐变还是突变，都将涉及功和能量问题，对卫星做正功，卫星机械能增大，由低轨道进入高轨道；对卫星做负功，卫星机械能减小，由高轨道进入低轨道。
七、功与能
1．几种力做功的特点
(1)重力、弹簧弹力、静电力做功与路径无关。
(2)摩擦力做功的特点
①单个摩擦力(包括静摩擦力和滑动摩擦力)可以做正功，也可以做负功，还可以不做功。
②相互作用的一对静摩擦力做功的代数和总等于零，在静摩擦力做功的过程中，只有机械能的转移，没有机械能转化为其他形式的能；相互作用的一对滑动摩擦力做功的代数和不为零，且总为负值。在一对滑动摩擦力做功的过程中，不仅有相互摩擦的物体间机械能的转移，还有部分机械能转化为内能，转化为内能的量等于系统机械能的减少量，等于滑动摩擦力与相对路程的乘积。
③摩擦生热是指滑动摩擦生热，静摩擦不会生热。
2．几个重要的功能关系
八、动量
(1)恒力冲量的计算：用公式I＝Ft。
(2)变力冲量的计算：方向不变的变力的冲量，若力的大小随时间均匀变化，即力为时间的一次函数，则力F在某段时间t内的冲量I＝eq \f(F1＋F2,2)t，其中F1、F2为该段时间内初、末两时刻力的大小。
(3)合冲量的计算
①若合外力是恒力，可先求出合力，再由F合t求冲量。
②若受几个力，且几个力均为恒力，可用F1t＋F2t＋…(矢量和)求冲量。
③若在全过程中受力情况不同，对应时间不同，可求每个力的冲量，然后矢量合成，即利用F1t1＋F2t2＋…(矢量和)求冲量。
④用动量定理I＝Δp求解。
(4)动量定理：物体所受合外力的冲量等于物体的动量变化，即I＝Δp。
(5)动量守恒定律的表达形式：
①m1v1＋m2v2＝m1v1′＋m2v2′，即p1＋p2＝p1′＋p2′；②Δp1＋Δp2＝0，Δp1＝－Δp2
(6)关于弹性碰撞的分析
两球发生弹性碰撞时满足动量守恒定律和机械能守恒定律。
在光滑的水平面上，质量为m1的钢球沿一条直线以速度v0与静止在水平面上的质量为m2的钢球发生弹性碰撞，碰后的速度分别是v1、v2
m1v0＝m1v1＋m2v2 ①
eq \f(1,2)m1veq \\al(2,0)＝eq \f(1,2)m1veq \\al(2,1)＋eq \f(1,2)m2veq \\al(2,2) ②
由①②可得
v1＝eq \f(m1－m2,m1＋m2)v0 ③
v2＝eq \f(2m1,m1＋m2)v0 ④
利用③式和④式，可讨论以下五种特殊情况
(a)当m1＞m2时，v1＞0，v2＞0，两钢球沿原方向运动；
(b)当m1＜m2时，v1＜0，v2＞0，质量较小的钢球被反弹，质量较大的钢球向前运动；
(c)当m1＝m2时，v1＝0，v2＝v0，两钢球交换速度；
(d)当m1≪m2时，v1≈v0，v2≈0，m1很小时，几乎以原速率被反弹回来，而质量很大的m2几乎不动。例如橡皮球与墙壁的碰撞；
(e)当m1≫m2时，v≈v0，v2≈2v0，说明m1很大时速度几乎不变，而质量很小的m2获得的速度是原来运动物体速度的2倍，这是原来静止的钢球通过碰撞可以获得的最大速度，例如铅球碰乒乓球。
九、电场
(1)库仑定律F＝keq \f(q1q2,r2)
(2)电场强度的表达式
①定义式E＝eq \f(F,q)
②点电荷的场强公式E＝eq \f(kQ,r2)
③匀强电场中E＝eq \f(U,d)
(3)电势差和电势的关系UAB＝φA－φB或UBA＝φB－φA
(4)静电力做功的计算
①普适WAB＝qUAB
②匀强电场W＝qEd
(5)电势能Ep＝qφ，注意q的正负。
(6)电容的定义式C＝eq \f(Q,U)＝eq \f(ΔQ,ΔU)，
电容器的决定式C＝eq \f(εrS,4πkd)
(7)电容器动态分析
①电容器接在电源上，电压不变；
②断开电源时，电容器电量不变；改变两板距离，E＝eq \f(4πkQ,εrS)，故场强不变；
③含二极管的电容器问题：如右图，若将A极板向上移动，由于二极管的存在，电容器无法放电，Q不变，C减小，则极板间电压U增大。
(8)静电计是测量电压U的仪器，题目往往将它与电容器一起考察。
(9)电场中的图像问题——φ－x图像和E－x图像
(10)等量同种(异种)点电荷的电场线和等势面分布图
十、磁场
(1)安培定则、左手定则、右手定则的应用(左力右电)。
(2)几种常见的磁感线分布
(3)磁感应强度的定义式B＝eq \f(F,Il)，安培力大小F＝IlB(B、I、l相互垂直，且l为有效长度)
(4)同向电流相互吸引，反向电流相互排斥(如下图)
1．有界磁场问题
单直线边界磁场
(1)进入型：带电粒子以一定速度v垂直于磁感应强度B进入磁场。
图1
图2
规律要点：①对称性：若带电粒子以与边界成θ角的速度进入磁场，则一定以与边界成θ角的速度离开磁场，如图1所示。
②完整性：比荷相等的正、负带电粒子以相同速度进入同一匀强磁场，则它们运动的圆弧轨道恰构成一个完整的圆。
(2)射出型：粒子源在磁场中，且可以向纸面内各个方向以相同速率发射同种带电粒子。
规律要点：(以图2中带负电粒子的运动轨迹为例)
①最值相切：当带电粒子的运动轨迹小于eq \f(1,2)圆周时且与边界相切(如图2中a点)，则切点为带电粒子不能射出磁场的最值点(或恰能射出磁场的临界点)；
②最值相交：当带电粒子的运动轨迹大于或等于eq \f(1,2)圆周时，直径与边界相交的点(图2中的b点)为带电粒子射出边界的最远点。
双直线边界磁场的规律要点
最值相切：当粒子源在一条边界上向纸面内各个方向以相同速率发射同一种粒子时，粒子能从另一边界射出的上、下最远点对应的轨道分别与两直线相切。如图3所示。
图3
对称性：过粒子源S的垂线为ab的中垂线。
在图3中，ab之间有带电粒子射出，可求得ab＝2eq \r(r2－（d－r）2)＝2eq \r(2dr－d2)
最值相切规律可推广到矩形区域磁场中。
圆形边界
(1)圆形磁场区域规律要点
①相交于圆心：带电粒子沿指向圆心的方向进入磁场，则出磁场时速度矢量的反向延长线一定过圆心，即两速度矢量相交于圆心；如图4。
②直径最小：以带电粒子轨迹圆弧对应的弦为直径所作的圆，即为最小圆形磁场区域。如图5所示。
③点入平出与平入点出：带电粒子从圆周上某点以相同速率沿不同方向射入磁场，若轨道半径R跟圆形磁场区半径r相等，则所有粒子沿与入射点切线平行的方向射出磁场(磁发散)，逆向也成立，即平入点出(磁聚焦)。如图6。
(2)环状磁场区域规律要点
①带电粒子沿(逆)半径方向射入磁场，若能返回同一边界，则一定逆(沿)半径方向射出磁场；
②最值相切：如图7，当带电粒子的运动轨迹与圆相切时，粒子有最大速度vm或磁场有最小磁感应强度B。
2．电磁技术六大实例
(1)【速度选择器】 如下左图，当带电粒子进入电场和磁场共存空间时，同时受到电场力和洛伦兹力作用，F电＝qE，F洛＝qv0B，若qE＝qBv0，有v0＝eq \f(E,B)，即能从S2孔飞出的粒子只有一种速度，而与粒子的质量、电性、电量无关。
(2)【电磁流量计】 如上右图，导电流体中的自由电荷(正负离子)在洛伦兹力作用下横向偏转，a、b间出现电势差。
由qvB＝qE＝qeq \f(U,d)可得v＝eq \f(U,Bd)
流量Q＝Sv＝eq \f(πd2,4)·eq \f(U,Bd)＝eq \f(πdU,4B)。
(3)【磁流体发电机】 如下左图，喷入磁场的正、负离子在洛伦兹力作用下发生上下偏转而聚焦到A、B板上，产生电势差，设A、B平行金属板的面积为S，相距为L，等离子气体的电阻率为ρ，喷入气体速度为v，板间磁场的磁感应强度为B，板外电阻为R，当等离子气体匀速通过A、B板间时，板间电势差最大，离子受力平衡：qE场＝qvB，E场＝vB，电动势E＝E场L＝BLv，电源内电阻r＝ρeq \f(L,S)，故R中的电流I＝eq \f(E,R＋r)＝eq \f(BLv,R＋ρ\f(L,S))＝eq \f(BLvS,RS＋ρL)。
(4)【霍尔效应】 如上右图，厚度为h，宽度为d的导体板放在垂直于磁感应强度为B的匀强磁场中，当电流流过导体板时，在导体板上下侧面间会产生电势差，U＝keq \f(IB,d)(k为霍尔系数)。(应重点注意载流子的区别：若为正电荷导电则A板电势较高，若为负电荷导电则A板电势较低)
(5)【回旋加速器】 如下图所示，是两个D形金属盒之间留有一个很小的缝隙，有很强的磁场垂直穿过D形金属盒。D形金属盒缝隙中存在交变的电场，带电粒子在缝隙的电场中被加速，然后进入磁场做半圆周运动。
①粒子在磁场中运动一周，被加速两次；交变电场的频率与粒子在磁场中圆周运动的频率相同。
T电场＝T回旋＝T＝eq \f(2πm,qB)。
②粒子在电场中每加速一次，都有qU＝ΔEk。
③粒子在边界射出时，都有相同的圆周半径R，有R＝eq \f(mv,qB)。
④粒子飞出加速器时的动能为Ek＝eq \f(mv2,2)＝eq \f(B2R2q2,2m)。在粒子质量、电量确定的情况下，粒子所能达到的最大动能只与加速器的半径R和磁感应强度B有关，与加速电压无关。
(6)【质谱仪】 粒子经加速电场加速后，从M点垂直于电场方向进入静电分析器，沿半径为R的四分之一圆弧轨道做匀速圆周运动，从N点射出，接着由P点垂直磁分析器的左边界射入，最后垂直于下边界从Q点射出并进入收集器
十一、闭合电路欧姆定律
1．闭合电路欧姆定律I＝eq \f(E,R＋r)。
2．路端电压与电流的关系U＝E－Ir。
3．电源的功率及效率问题
十二、法拉第电磁感应定律
(1)法拉第电磁感应定律应用的三种情况
①ΔΦ＝B·ΔS，则E＝neq \f(BΔS,Δt)。
②ΔΦ＝ΔB·S，则E＝neq \f(ΔB·S,Δt)。
③ΔΦ＝Φ末－Φ初，E＝neq \f(B2S2－B1S1,Δt)≠neq \f(ΔB·ΔS,Δt)。
(2)在Φ－t图像中磁通量的变化率eq \f(ΔΦ,Δt)是图像上某点切线的斜率，利用斜率和线圈匝数可以确定该点感应电动势的大小。
(3)导体垂直切割磁感线时，E＝Blv，式中l为导体切割磁感线的有效长度。
(4)导体棒以端点为轴，在匀强磁场中垂直于磁感线方向匀速转动产生感应电动势E＝eq \f(1,2)Bl2ω。
(5)电磁感应现象中通过导体截面的电量
q＝IΔt＝neq \f(ΔΦ,R)。
(6)电磁感应与电路问题：如下图，注意电路的串并联结构、电源的正负极、电源内阻、外电压等。
(7)求电荷量的三种方法
(8)电磁感应中处理变加速运动的两种方法
①动量定理mv＝IlB·Δt＝Blq＝Bl·eq \f(Blx,R总)
②动能定理eq \f(1,2)mv2－eq \f(1,2)mveq \\al(2,0)＝W合＝F合·x
【注】 对于力随时间或力随位移线性变化的情况，可以画出F－x或F－t图像，则图像围成的面积代表该力的功或者冲量。
(9)电磁感应中的两条重要关系
①安培力与速度的关系F安＝eq \f(B2l2,R总)v(对于匀强磁场，安培力与速度成正比)
②变加速运动中时间与位移的关系F安·t＝IlB·t＝Blq＝Bl·(neq \f(ΔΦ,R总))＝Bl·(neq \f(Blx,R总))
十三、交变电流
1．正弦式交流电有效值的求解
利用I＝eq \f(Im,\r(2))，U＝eq \f(Um,\r(2))，E＝eq \f(Em,\r(2))计算。
2．理想变压器的基本关系式
(1)功率关系：P入＝P出。
(2)电压关系：eq \f(U1,U2)＝eq \f(n1,n2)。
(3)电流关系：只有一个副线圈时，eq \f(I1,I2)＝eq \f(n2,n1)；有多个副线圈时，U1I1＝U2I2＋U3I3＋…＋UnIn。
3．远距离输电
(1)原理图
(2)输电流程
如图所示，注意流程的决定方向，电压由发电机开始，发电机的输出电压＝升压变压器的输入电压eq \(――→,\s\up7(决定))升压变压器的输出电压－U损＝降压变压器的输入电压eq \(――→,\s\up7(决定))降压变压器的输出电压＝用户电压；功率和电流的流程方向相反，由用户决定，这是远距离输电的另一个要点。
(3)分析三个回路：在每个回路中变压器的原线圈是回路的用电器，而相应的副线圈是下一个回路的电源。
(4)综合运用下面三个方面的关系求解
①能量关系
P＝U1I1＝U2I2＝P用＋P损
P损＝Ieq \\al(2,2)r
P用＝U3I3＝U4I4
②电压关系
U2＝ΔU＋U3
ΔU＝I2r。
③变压比关系
eq \f(U1,U2)＝eq \f(I2,I1)＝eq \f(n1,n2)
eq \f(U3,U4)＝eq \f(I4,I3)＝eq \f(n3,n4)。
(5)输电线损失
远距离输电的要点之一是输电线损失，功率损失为P额＝I2r＝eq \f(P2,U2)r，电压损失为U损＝Ir，其中U、I分别为高压输电电压和电流，最容易错写成P损＝IU。
十四、电磁场和电磁波
十五、热学
十六、振动和波
1．物体做简谐振动
在平衡位置达到最大值的量有速度、动量、动能。
在最大位移处达到最大值的量有回复力、加速度、势能。
通过同一点有相同的位移、速率、回复力、加速度、动能、势能，只可能有不同的运动方向。
经过半个周期，物体运动到对称点，速度大小相等、方向相反。
半个周期内回复力的总功为零，总冲量为2mvt，路程为2倍振幅。
经过一个周期，物体运动到原来位置，一切参量恢复。
一个周期内回复力的总功为零，总冲量为零。路程为4倍振幅。
2．波传播过程中介质质点都作受迫振动，都重复振源的振动，只是开始时刻不同。
波源先向上运动，产生的横波波峰在前；波源先向下运动，产生的横波波谷在前。
波的传播方式：前端波形不变，向前平移并延伸。
3．由波的图像讨论波的传播距离、时间、周期和波速等时：注意“双向”和“多解”。
4．波形图上，介质质点的运动方向：“上坡向下，下坡向上”。
5．波进入另一介质时，频率不变、波长和波速改变，波长与波速成正比。
6．波发生干涉时，看不到波的移动。振动加强点和振动减弱点位置不变，互相间隔。
十七、光的折射与全反射
1．折射率
(1)定义式：n＝eq \f(sin θ1,sin θ2)。
(2)计算公式：n＝eq \f(c,v)，因为vv1，在B点加速，则v3>vB，又因v1>v3，故有vA>v1>v3>vB。
②加速度：因为在A点，卫星只受到万有引力作用，故不论从轨道Ⅰ还是轨道Ⅱ上经过A点，卫星的加速度都相同，同理，卫星在轨道Ⅱ或Ⅲ上经过B点的加速度也相同。
③周期：设卫星在Ⅰ、Ⅱ、Ⅲ轨道上的运行周期分别为T1、T2、T3，轨道半径分别为r1、r2(半长轴)、r3，由开普勒第三定律eq \f(r3,T2)＝k可知T1