浙江省温州市苍南县灵溪学区2024—2025学年上学期期中考试七年级数学试卷

这是一份浙江省温州市苍南县灵溪学区2024—2025学年上学期期中考试七年级数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）﹣2024的倒数是（ ）
A．﹣2024B．2024C．D．
2．（3分）负数的概念最早出现在《九章算术》中，把向东走2km记做“+2km”，向西走1km应记做（ ）
A．﹣2kmB．﹣1kmC．1kmD．+2km
3．（3分）据报道，2024年国庆假期期间，全国国内出游人数约765000000，将数据765000000用科学记数法表示为（ ）
A．7.65×108B．7.65×107C．76.5×107D．0.765×109
4．（3分）在数1，0，﹣3，﹣2中，最小的数是（ ）
A．﹣3B．0C．1D．﹣2
5．（3分）浙教版初中数学课本长度约为25.8cm，该近似数25.8精确到（ ）
A．千分位B．百分位C．十分位D．个位
6．（3分）实数在哪两个相邻的整数之间（ ）
A．0和1之间B．1和2之间C．2和3之间D．3和4之间
7．（3分）下列各式计算正确的是（ ）
A．＝±5B．
C．（﹣1）4＝﹣1D．＝﹣2
8．（3分）为落实“双减”政策，某校利用课后服务开展了主题为“书香满校圆”的读书活动．现需购买甲、乙两种读本共80本供学生阅读，其中甲种读本的价格为10元/本，乙种读本的价格为8元/本，若购买甲种读本x本，则购买乙种读本的费用为（ ）
A．8（80﹣x）元B．10（80﹣x）元
C．8x元D．（80﹣8x）元
9．（3分）下列问题情境，能用加法算式﹣2+10表示的是（ ）
A．水位先下降2cm，又下降10cm后的水位变化情况
B．将原点先向左移动10个单位长度，再向右移动2个单位长度后表示的数
C．用10元纸币购买2元文具后找回的零钱
D．数轴上表示﹣2与10的两个点之间的距离
10．（3分）对于实数x，我们规定[x]表示不大于x的最大整数，如[2]＝2，[1.5]＝1，[﹣2.3]＝﹣3．对数99进行如下操作：99[]＝9[]＝3[]＝1，这样对数99只需进行3次操作后变成1，类似地，使数2024变为1需要进行操作的次数是（ ）
A．3B．4C．5D．6
二、填空题（本题共8小题，每小题3分，共24分）
11．（3分）的算术平方根为 ．
12．（3分）用代数式表示：m的3倍与n的差为 ．
13．（3分）比较大小（用“＞”或”＜”表示）﹣ ．
14．（3分）若（a+1）2+|b﹣3|＝0，则ab＝ ．
15．（3分）若一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动7个单位长度，此时终点所表示的数是 ．
16．（3分）用“☆”定义一种新运算：对于任意有理数a和b，规定a☆b＝ab2+a．如：1☆3＝1×32+1＝10．则（﹣2）☆3的值为 ．
17．（3分）已知在纸面上有一数轴（如图所示），折叠纸面，使O表示的点与2表示的点重合，则8表示的点与数 表示的点重合．
18．（3分）为了让学生更好的掌握第二章有理数的运算知识，七年（1）班数学老师在班级里组织了一次知识竞赛，有10道选择题，每道题答对得5分，答错或不答扣1分．
（1）小明答对了8道题，答错了2道题，他的总得分是 分；
（2）若该班的学生中至少有4人的得分相同，则这个班级的学生至少有 人．
三、解答题（本题共有6小题，共46分，解答需要写出必要的文字说明、演算步骤或说理过程。）
19．（9分）计算：
（1）3+（﹣2）﹣（﹣3）．
（2）+|﹣3|．
（3）2×（﹣32）﹣4÷（﹣）．
20．（6分）简便计算：
（1）；
（2）．
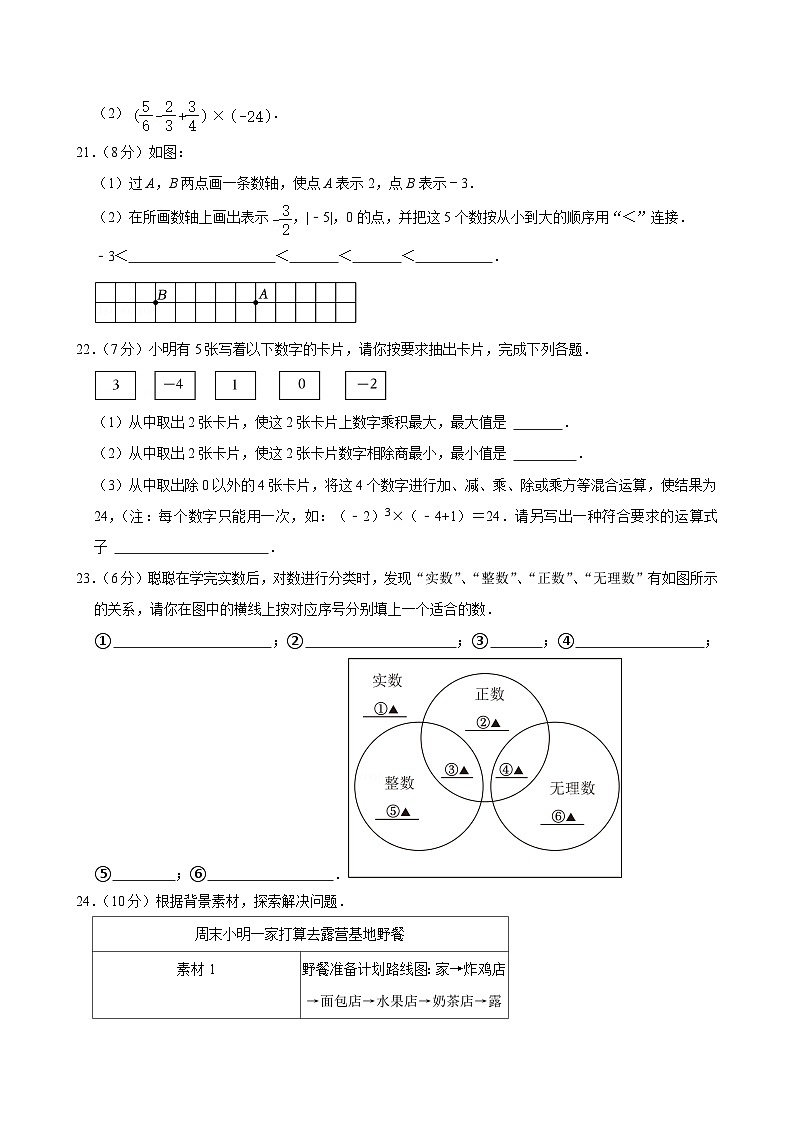
21．（8分）如图：
（1）过A，B两点画一条数轴，使点A表示2，点B表示﹣3．
（2）在所画数轴上画出表示，|﹣5|，0的点，并把这5个数按从小到大的顺序用“＜”连接．
﹣3＜ ＜ ＜ ＜ ．
22．（7分）小明有5张写着以下数字的卡片，请你按要求抽出卡片，完成下列各题．
（1）从中取出2张卡片，使这2张卡片上数字乘积最大，最大值是 ．
（2）从中取出2张卡片，使这2张卡片数字相除商最小，最小值是 ．
（3）从中取出除0以外的4张卡片，将这4个数字进行加、减、乘、除或乘方等混合运算，使结果为24，（注：每个数字只能用一次，如：（﹣2）3×（﹣4+1）＝24．请另写出一种符合要求的运算式子 ．
23．（6分）聪聪在学完实数后，对数进行分类时，发现“实数”、“整数”、“正数”、“无理数”有如图所示的关系，请你在图中的横线上按对应序号分别填上一个适合的数．
① ；② ；③ ；④ ；⑤ ；⑥ ．
24．（10分）根据背景素材，探索解决问题．
2024-2025学年浙江省温州市苍南县灵溪学区七年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本题有10小题，每小题3分，共30分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）。
1．（3分）﹣2024的倒数是（ ）
A．﹣2024B．2024C．D．
【答案】C
【分析】根据题意利用倒数定义即可得出本题答案．
【解答】解：∵，
故选：C．
【点评】本题考查倒数定义，解题的关键是掌握倒数的定义．
2．（3分）负数的概念最早出现在《九章算术》中，把向东走2km记做“+2km”，向西走1km应记做（ ）
A．﹣2kmB．﹣1kmC．1kmD．+2km
【答案】B
【分析】利用正数、负数的意义解答即可．
【解答】解：∵向东走2km记做“+2km”，
∴向西走1km应记做：﹣1km．
故选：B．
【点评】本题考查了正数、负数，解题的关键是掌握正数、负数的意义．
3．（3分）据报道，2024年国庆假期期间，全国国内出游人数约765000000，将数据765000000用科学记数法表示为（ ）
A．7.65×108B．7.65×107C．76.5×107D．0.765×109
【答案】A．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：765000000＝7.65×108．
故选：A．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
4．（3分）在数1，0，﹣3，﹣2中，最小的数是（ ）
A．﹣3B．0C．1D．﹣2
【答案】A
【分析】先根据有理数的大小比较法则比较四个数的大小，再得出答案即可．
【解答】解：∵﹣3＜﹣2＜0＜1，
∴最小的数是﹣3，
故选：A．
【点评】本题考查了有理数的大小比较，能熟记知识点是解此题的关键，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．
5．（3分）浙教版初中数学课本长度约为25.8cm，该近似数25.8精确到（ ）
A．千分位B．百分位C．十分位D．个位
【答案】C
【分析】根据近似数小数部分的最后一位即可判断．
【解答】解：根据精确度的定义可知，近似数25.8精确到十分位，
故答案为：C．
【点评】本题考查近似数的精确度，掌握四舍五入是关键．
6．（3分）实数在哪两个相邻的整数之间（ ）
A．0和1之间B．1和2之间C．2和3之间D．3和4之间
【答案】C
【分析】根据算术平方根的定义，估算无理数的大小即可．
【解答】解：∵4＜5＜9，
∴，
即2＜＜3，
故选：C．
【点评】本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的前提．
7．（3分）下列各式计算正确的是（ ）
A．＝±5B．
C．（﹣1）4＝﹣1D．＝﹣2
【答案】D
【分析】根据算术平方根、有理数的乘方、立方根的定义逐项计算判断即可．
【解答】解：A、，故此选项不符合题意；
B、，，所以，故此选项不符合题意；
C、（﹣1）4＝1，故此选项不符合题意；
D、，故此选项符合题意；
故选：D．
【点评】本题考查了立方根、算术平方根、有理数的乘方，熟练掌握运算法则是解题的关键．
8．（3分）为落实“双减”政策，某校利用课后服务开展了主题为“书香满校圆”的读书活动．现需购买甲、乙两种读本共80本供学生阅读，其中甲种读本的价格为10元/本，乙种读本的价格为8元/本，若购买甲种读本x本，则购买乙种读本的费用为（ ）
A．8（80﹣x）元B．10（80﹣x）元
C．8x元D．（80﹣8x）元
【答案】A
【分析】根据题意和题目中的数据，可以用含x的代数式表示出购买乙种读本的费用．
【解答】解：由题意可得，
购买乙种读本的费用为8（80﹣x）元，
故选：A．
【点评】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．
9．（3分）下列问题情境，能用加法算式﹣2+10表示的是（ ）
A．水位先下降2cm，又下降10cm后的水位变化情况
B．将原点先向左移动10个单位长度，再向右移动2个单位长度后表示的数
C．用10元纸币购买2元文具后找回的零钱
D．数轴上表示﹣2与10的两个点之间的距离
【答案】C
【分析】根据有理数的加减运算进行判断，注意正负数的相对意义．
【解答】解：A：水位两次变化均为下降，故2和10前面的正负号应保持一致，不符合题意；
B：将原点先向左移动10个单位长度，再向右移动2个单位长度后表示的数为：﹣10+2，不符合题意；
C：设支出为负，收入为正，则用10元纸币购买2元文具后找回的零钱为：﹣2+10，符合题意；
D：数轴上表示﹣2与10的两个点之间的距离为：10﹣（﹣2），不符合题意．
故选：C．
【点评】本题考查有理数的加减运算的实际应用．掌握有理数的加减运算法则是关键．
10．（3分）对于实数x，我们规定[x]表示不大于x的最大整数，如[2]＝2，[1.5]＝1，[﹣2.3]＝﹣3．对数99进行如下操作：99[]＝9[]＝3[]＝1，这样对数99只需进行3次操作后变成1，类似地，使数2024变为1需要进行操作的次数是（ ）
A．3B．4C．5D．6
【答案】B
【分析】根据题目中所提供的方法进行计算即可．
【解答】解：根据题目中所提供的方法进行计算，进行4次操作后变成1，
故选：B．
【点评】本题考查估算无理数的大小，理解[x]的定义以及题目中所提供的运算是正确解答的前提．
二、填空题（本题共8小题，每小题3分，共24分）
11．（3分）的算术平方根为 2 ．
【答案】见试题解答内容
【分析】根据算术平方根的定义进行解题即可．
【解答】解：∵＝4，
∴的算术平方根是2．
故答案为：2．
【点评】此题主要考查了算术平方根的性质和应用，要熟练掌握，解答此题的关键是要明确：①被开方数a是非负数；②算术平方根a本身是非负数．求一个非负数的算术平方根与求一个数的平方互为逆运算，在求一个非负数的算术平方根时，可以借助乘方运算来寻找．
12．（3分）用代数式表示：m的3倍与n的差为 3m﹣n ．
【答案】3m﹣n．
【分析】根据题意，用代数式表示即可．
【解答】解：∵m的3倍表示为3m，
∴m的3倍与n的差为3m﹣n．
故答案为：3m﹣n．
【点评】本题考查了代数式的表示，熟练用代数式表示出所求的量是解题的关键．
13．（3分）比较大小（用“＞”或”＜”表示）﹣ ＜ ．
【答案】见试题解答内容
【分析】根据“正数大于0，负数小于0，正数大于负数”便可直接解答．
【解答】解：∵﹣＜0，＞0，
∴﹣＜．
【点评】解答此类题目的关键是熟知以下知识：
（1）在以向右方向为正方向的数轴上两点，右边的点表示的数比左边的点表示的数大；
（2）正数大于0，负数小于0，正数大于负数；
（3）两个正数中绝对值大的数大；
（4）两个负数中绝对值大的反而小．
14．（3分）若（a+1）2+|b﹣3|＝0，则ab＝ ﹣1 ．
【答案】见试题解答内容
【分析】根据非负数的性质列出方程求出a、b的值，代入所求代数式计算即可．
【解答】解：∵（a+1）2+|b﹣3|＝0，
∴，
解得，
∴ab＝（﹣1）3＝﹣1，
故答案为﹣1．
【点评】本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
15．（3分）若一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动7个单位长度，此时终点所表示的数是 ﹣4 ．
【答案】见试题解答内容
【分析】根据右移加，左移减，列式得出答案．
【解答】解：由题意得：0+3﹣7＝﹣4，
则此时终点所表示的数是﹣4．
故答案为：﹣4．
【点评】本题考查了数轴上两点之间的距离公式，掌握数轴的定义是解本题的关键．
16．（3分）用“☆”定义一种新运算：对于任意有理数a和b，规定a☆b＝ab2+a．如：1☆3＝1×32+1＝10．则（﹣2）☆3的值为 ﹣20 ．
【答案】﹣20．
【分析】原式利用题中的新定义计算即可求出值．
【解答】解：根据题中的新定义得：
原式＝﹣2×32+（﹣2）
＝﹣18﹣2
＝﹣20．
故答案为：﹣20．
【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
17．（3分）已知在纸面上有一数轴（如图所示），折叠纸面，使O表示的点与2表示的点重合，则8表示的点与数 ﹣6 表示的点重合．
【答案】﹣6．
【分析】利用数轴知识解答．
【解答】解：∵O表示的点与2表示的点重合，
∴可以知道是沿着1折叠的，
∴8﹣1＝7，1﹣7＝﹣6，
∴8表示的点与数﹣6表示的点重合．
故答案为：﹣6．
【点评】本题考查了数轴，解题的关键是掌握数轴知识．
18．（3分）为了让学生更好的掌握第二章有理数的运算知识，七年（1）班数学老师在班级里组织了一次知识竞赛，有10道选择题，每道题答对得5分，答错或不答扣1分．
（1）小明答对了8道题，答错了2道题，他的总得分是 38 分；
（2）若该班的学生中至少有4人的得分相同，则这个班级的学生至少有 34 人．
【答案】（1）38；
（2）34．
【分析】（1）利用小明的总得分＝5×答对题目数﹣1×答错题目数，即可求出结论；
（2）由试题的题目数及“每道题答对得5分，答错或不答扣1分”，可得出共有11种不同的分值，再利用抽屉原理，即可得出结论．
【解答】解：（1）根据题意得：5×8﹣1×2
＝40﹣2
＝38（分），
∴小明的总得分是38分．
故答案为：38；
（2）∵该知识竞赛有10道选择题，每道题答对得5分，答错或不答扣1分，
∴共有10+1＝11（种）不同的分值，
∴为了保证该班的学生中至少有4人的得分相同，这个班级的学生至少有11×3+1＝34（人）．
故答案为：34．
【点评】本题考查了抽屉原理的实际应用以及有理数的混合运算，从最差情况出发，求出这个班级的最少人数是解题的关键．
三、解答题（本题共有6小题，共46分，解答需要写出必要的文字说明、演算步骤或说理过程。）
19．（9分）计算：
（1）3+（﹣2）﹣（﹣3）．
（2）+|﹣3|．
（3）2×（﹣32）﹣4÷（﹣）．
【答案】（1）4；
（2）2；
（3）﹣6．
【分析】（1）先把减法运算变为加法运算，再根据有理数加法法则计算即可；
（2）先根据算术平方根、立方根、绝对值的定义计算，再根据有理数加减法则计算即可；
（3）先算乘方，再算乘除，最后算加减．
【解答】解：（1）3+（﹣2）﹣（﹣3）
＝3+（﹣2）+3
＝4；
（2）
＝2﹣3+3
＝2；
（3）
＝2×（﹣9）﹣4×（﹣3）
＝﹣18﹣（﹣12）
＝﹣18+12
＝﹣6．
【点评】本题考查了实数的运算，熟练掌握相关运算法则是解题的关键．
20．（6分）简便计算：
（1）；
（2）．
【答案】（1）﹣1；
（2）﹣22．
【分析】（1）根据有理数加法交换律和结合律求解即可；
（2）根据有理数乘法分配律求解即可．
【解答】解：（1）
＝
＝﹣1+0
＝﹣1；
（2）
＝
＝﹣20+16﹣18
＝﹣22．
【点评】本题主要考查了有理数的混合运算，解题的关键是运算定律的运用．
21．（8分）如图：
（1）过A，B两点画一条数轴，使点A表示2，点B表示﹣3．
（2）在所画数轴上画出表示，|﹣5|，0的点，并把这5个数按从小到大的顺序用“＜”连接．
﹣3＜ ﹣ ＜ 0 ＜ 2 ＜ |﹣5| ．
【答案】（1）见解答；
（2）见解答，﹣，0，2，|﹣5|．
【分析】（1）利用数轴知识解答；
（2）利用数轴知识和有理数的大小比较解答．
【解答】解：（1）
（2），
．
故答案为：﹣，0，2，|﹣5|．
【点评】本题考查了数轴和有理数的大小比较，解题的关键是掌握数轴知识和有理数的大小比较方法．
22．（7分）小明有5张写着以下数字的卡片，请你按要求抽出卡片，完成下列各题．
（1）从中取出2张卡片，使这2张卡片上数字乘积最大，最大值是 8 ．
（2）从中取出2张卡片，使这2张卡片数字相除商最小，最小值是 ﹣4 ．
（3）从中取出除0以外的4张卡片，将这4个数字进行加、减、乘、除或乘方等混合运算，使结果为24，（注：每个数字只能用一次，如：（﹣2）3×（﹣4+1）＝24．请另写出一种符合要求的运算式子 （﹣2）3×（﹣4+1）＝24 ．
【答案】（1）8；（2）﹣2；（3）（﹣2）3×（﹣4+1）＝24．
【分析】（1）找出﹣4与﹣2，使其乘积最大即可；
（2）找出﹣4与1，使其商最小即可；
（3）利用“24点”游戏规则写出两个符合要求的式子即可．
【解答】解：（1）从中取出2张卡片，使这2张卡片上数字乘积最大，﹣2×（﹣4）＝8；
（2）从中取出2张卡片，使这2张卡片数字相除商最小，﹣4÷1＝﹣4；
（3）从中取出除0以外的4张卡片，将这4个数字进行加、减、乘、除或乘方等混合运算，使结果为24，例如，（﹣2）3×（﹣4+1）＝24；
故答案为：（1）8；（2）﹣2；（3）（﹣2）3×（﹣4+1）＝24．
【点评】此题考查了有理数的混合运算，掌握有理数的混合运算法则是解本题的关键．
23．（6分）聪聪在学完实数后，对数进行分类时，发现“实数”、“整数”、“正数”、“无理数”有如图所示的关系，请你在图中的横线上按对应序号分别填上一个适合的数．
① ﹣ ；② ；③ 1 ；④ ；⑤ ﹣1 ；⑥ ﹣ ．
【答案】①﹣；②；③1：④；⑤﹣1；⑥﹣．（答案不唯一）．
【分析】根据实数的分类即可得出答案．
【解答】解：①﹣；②；③1：④；⑤﹣1；⑥﹣．（答案不唯一）．
故答案为：①﹣；②；③1：④；⑤﹣1；⑥﹣．（答案不唯一）．
【点评】此题主要考查了实数的分类．实数分为：有理数和无理数；有理数分为：整数和分数；无理数分为：正无理数、负无理数（无限不循环小数）．
24．（10分）根据背景素材，探索解决问题．
【答案】（1）11.5km；
（2）12元；
（3）水果店到奶茶店用8折券，奶茶店到露营基地用7折券，共用车费57.8元．
【分析】（1）根据正数和负数的实际意义列式计算即可；
（2）根据正数和负数的实际意义列式计算即可；
（3）根据题意列式计算即可．
【解答】解：（1）﹣3+6+2.5﹣5﹣12＝﹣11.5（km），
即露营基地在家的西边11.5km处；
（2）8+（6﹣3）×2＝14（元），
即炸鸡店到面包店所需费用12元；
（3）∵8+（5﹣3）×2＝12元，8+（12﹣3）×2＝26元，8＜12＜26，
∴8+14+8+[8+（5﹣3）×2]×0.8+[8+（12﹣3）×2]×0.7＝57.8（元）
即水果店到奶茶店用8折券，奶茶店到露营基地用7折券，共用车费57.8元．
【点评】本题考查有理数的混合运算，正数和负数，结合已知条件列得正确的算式是解题的关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/25 0:15:54；用户：13551613617；邮箱：13551613617；学号：60190894周末小明一家打算去露营基地野餐
素材1
野餐准备计划路线图：家→炸鸡店→面包店→水果店→奶茶店→露营基地；
素材2
这条路线近似看成东西走向．如果规定向东为正，向西为负，他这天行车里程（单位：km） 如下：
﹣3，+6，+2.5，﹣5，﹣12；
素材3
滴滴车价目表：起步价（不超过3km时）车费8元，超过3km时，超出部分每千米车费加价2元，原价消费满10元赠送一张8折优惠券和一张7折优惠券（每种优惠券只能使用一次）．
问题解决
任务1
求露营基地在家的哪个方向，并求出与家的距离：
任务2
计算炸鸡店到面包店所用的车费；
任务3
说说该路线如何正确使用优惠券，使总车费最低，并求出最低总车费.
周末小明一家打算去露营基地野餐
素材1
野餐准备计划路线图：家→炸鸡店→面包店→水果店→奶茶店→露营基地；
素材2
这条路线近似看成东西走向．如果规定向东为正，向西为负，他这天行车里程（单位：km） 如下：
﹣3，+6，+2.5，﹣5，﹣12；
素材3
滴滴车价目表：起步价（不超过3km时）车费8元，超过3km时，超出部分每千米车费加价2元，原价消费满10元赠送一张8折优惠券和一张7折优惠券（每种优惠券只能使用一次）．
问题解决
任务1
求露营基地在家的哪个方向，并求出与家的距离：
任务2
计算炸鸡店到面包店所用的车费；
任务3
说说该路线如何正确使用优惠券，使总车费最低，并求出最低总车费.