辽宁省沈阳市浑南区东北育才学校2024-2025学年九年级上学期11月月考数学试题

这是一份辽宁省沈阳市浑南区东北育才学校2024-2025学年九年级上学期11月月考数学试题，文件包含第二次学情调研答案docx、扫描件_2024-2025学年度上学期第二次学情数学pdf、扫描件_初三年级数学答题卡pdf等3份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
解：（1）原式＝
＝1+2﹣5+1
＝﹣1；
（2）原式＝
＝
＝
＝2（x﹣2）
＝2x﹣4．
17.(本小题8分)
解：(1)设每辆小客车的座位数是x个，每辆大客车的座位数是y个，根据题意可得：
y−x=154y+6x=310，
解得：x=25y=40．
答：每辆大客车的座位数是40个，每辆小客车的座位数是25个．
(2)设租用a辆小客车才能使所有参加活动的师生均有座位，则
25a+40(10−a)≥310+40，
解得：a≤313，
符合条件的a最大整数为3．
答：最多租用小客车3辆．
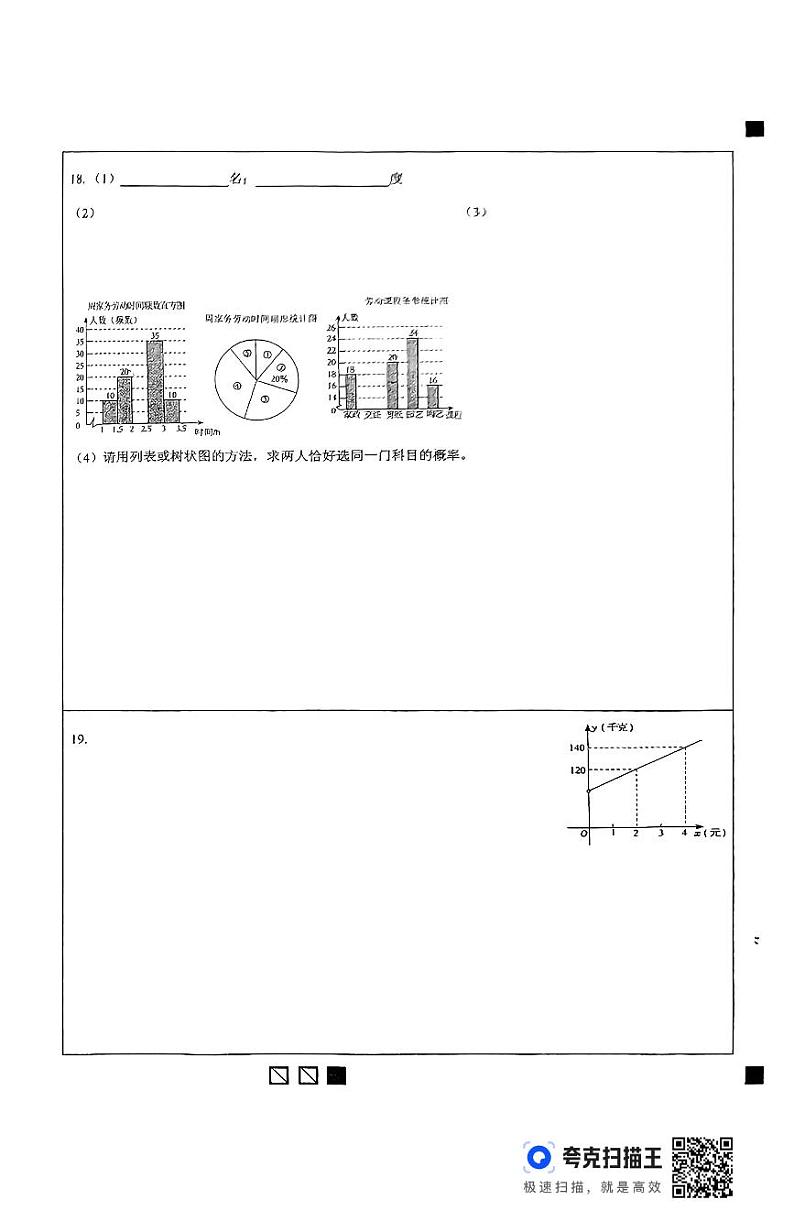
18、解：（1）参与本次问卷调查的学生人数为：20÷20%＝100（名），
第④组所对应扇形的圆心角的度数为：，
故答案为：100，126；
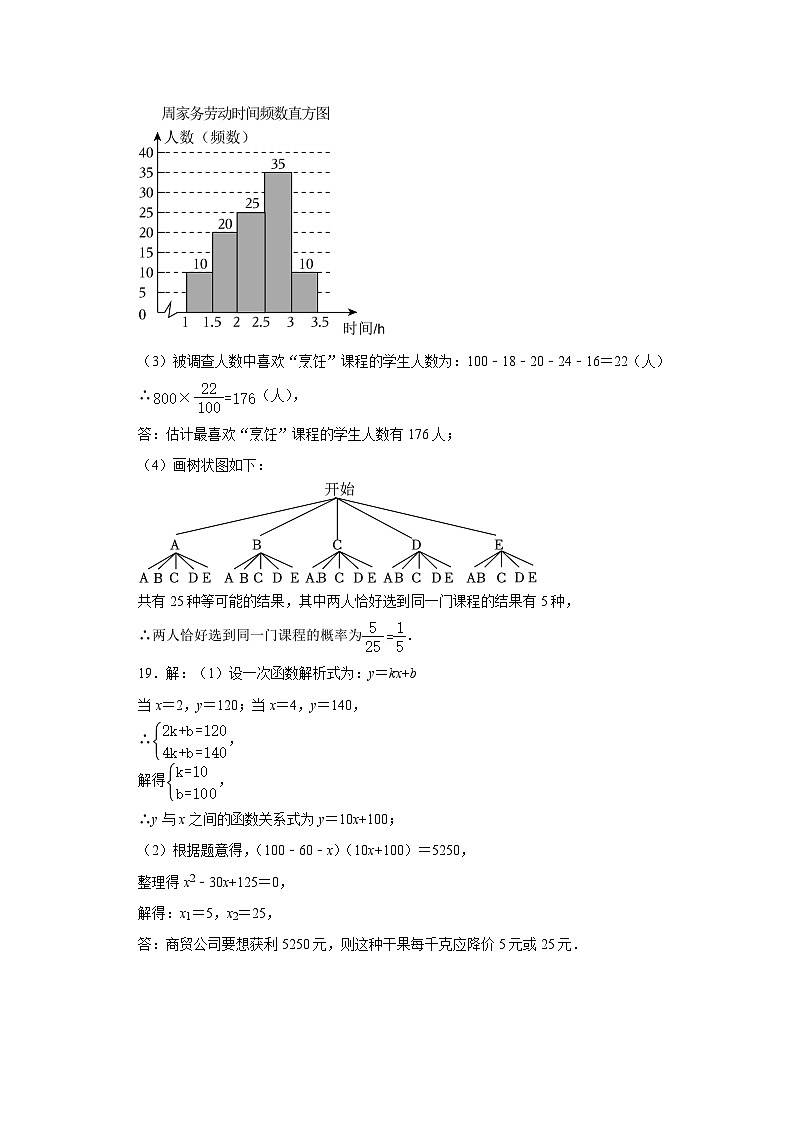
（2）第③组的人数为：100﹣10﹣20﹣35﹣10＝25（人），
补全周家务劳动时间的频数分布直方图如下：
（3）被调查人数中喜欢“烹饪”课程的学生人数为：100﹣18﹣20﹣24﹣16＝22（人）
∴（人），
答：估计最喜欢“烹饪”课程的学生人数有176人；
（4）画树状图如下：
共有25种等可能的结果，其中两人恰好选到同一门课程的结果有5种，
∴两人恰好选到同一门课程的概率为．
19．解：（1）设一次函数解析式为：y＝kx+b
当x＝2，y＝120；当x＝4，y＝140，
∴，
解得，
∴y与x之间的函数关系式为y＝10x+100；
（2）根据题意得，（100﹣60﹣x）（10x+100）＝5250，
整理得x2﹣30x+125＝0，
解得：x1＝5，x2＝25，
答：商贸公司要想获利5250元，则这种干果每千克应降价5元或25元．
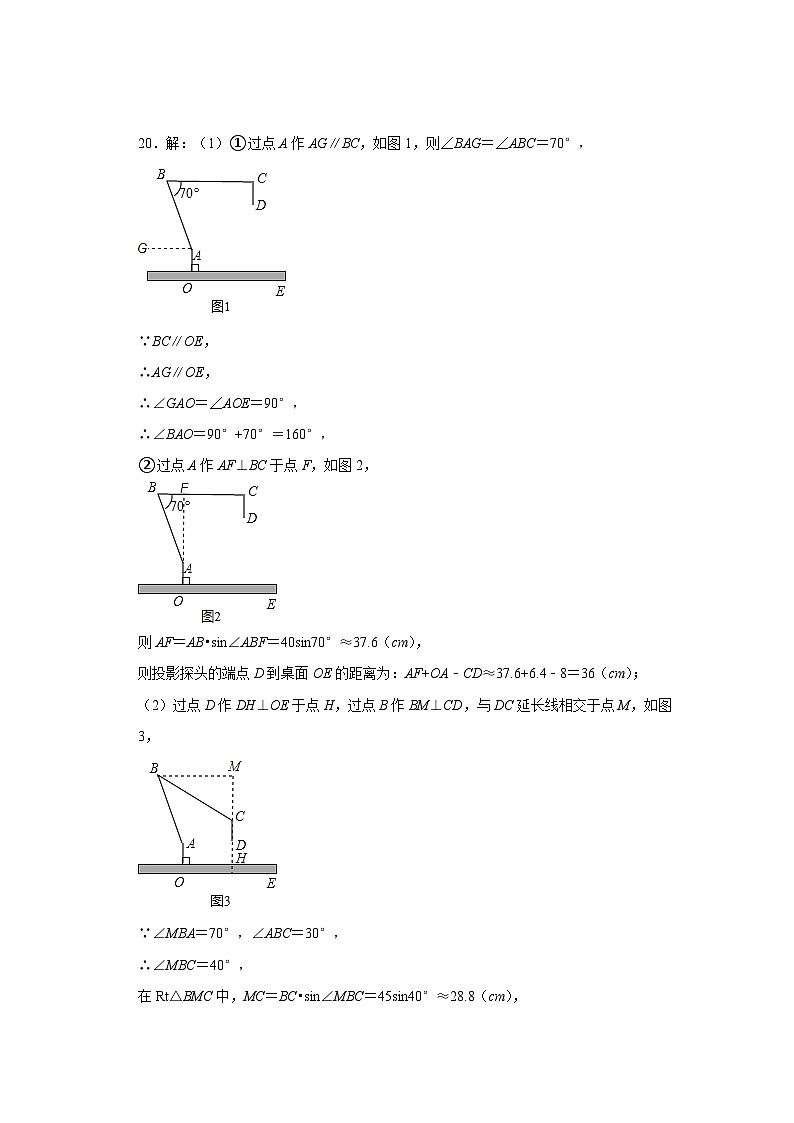
20．解：（1）①过点A作AG∥BC，如图1，则∠BAG＝∠ABC＝70°，
∵BC∥OE，
∴AG∥OE，
∴∠GAO＝∠AOE＝90°，
∴∠BAO＝90°+70°＝160°，
②过点A作AF⊥BC于点F，如图2，
则AF＝AB•sin∠ABF＝40sin70°≈37.6（cm），
则投影探头的端点D到桌面OE的距离为：AF+OA﹣CD≈37.6+6.4﹣8＝36（cm）；
（2）过点D作DH⊥OE于点H，过点B作BM⊥CD，与DC延长线相交于点M，如图3，
∵∠MBA＝70°，∠ABC＝30°，
∴∠MBC＝40°，
在Rt△BMC中，MC＝BC•sin∠MBC＝45sin40°≈28.8（cm），
则投影探头的端点D到桌面OE的距离≈CD+36﹣MC﹣CD≈36﹣28.8＝7.2（cm）．
故投影探头的端点D到桌面OE的距离约为7.2cm．
故答案为：160；36cm．
21、（1）证明：∵四边形ABCD是矩形，
∴BE＝DE，
∵OB＝OD，
∴OE⊥BD，
∴∠DEO＝∠DAO＝90°，
∵∠DFE＝∠AFO，
∴∠FDE＝∠AOF，
∵AO＝AD，∠DAB＝∠DAO＝90°，△AOF≌△ADB，
∴AF＝AB．
（2）解：由（1）得，△OAF≌△DAB，
∴AF＝AB，
连接BF，如图，
∴BF＝AF，
∵BE＝DE，OE⊥BD，
∴DF＝BF，
∴DF＝AF，
∴＝．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/12 10:49:36；用户：宋坤；邮箱：15040112280；学号：474230722、解：(1)(16+2 10) cm;
(2)74或13;
(3)①如图3，
若P在边AC上时，BC=CP=6cm，
此时用的时间为6s，△BCP为等腰三角形；
②若P在AB边上时，有三种情况：
i)如图4，
若使BP=CB=6cm，此时AP=4cm，P运动的路程为4+8=12cm，
所以用的时间为12s时，△BCP为等腰三角形；
ii)如图5，
若CP=BC=6cm，
过C作CD⊥AB于点D，
根据面积法12AC·BC=12AB·CD
得高CD=4.8cm，
在Rt△BCD中，BD= BC2−CD2=3.6cm，
∴BP=2BD=7.2cm，
∴P运动的路程为18−7.2=10.8cm，
∴用的时间为10.8s时，△BCP为等腰三角形；
ⅲ)如图6，
若BP=CP，则∠PCB=∠B，
∵∠ACP+∠BCP=90°，∠B+∠A=90°，
∴∠ACP=∠A，
∴PA=PC
∴PA=PB=5cm
∴P运动的路程为13cm，所以时间为13s时，△BCP为等腰三角形．
综上所述，当t为6或12或10.8或13时，△BCP为等腰三角形；
(4)分两种情况：①当P、Q相遇前：如图7，
P点走过的路程为tcm，Q走过的路程为2tcm，
∵直线PQ把△ABC的周长分成相等的两部分，
∴t+2t=12，
∴t=4；
②当P、Q相遇后：如图8，
当P点在AB上，Q在AC上，则AP=t−8，AQ=2t−16，
∵直线PQ把△ABC的周长分成相等的两部分，
∴t−8+2t−16=12，
∴t=12，
∴当t为4或12时，直线PQ把△ABC的周长分成相等的两部分．
23、解：（1）∵sin30°＝，cs45°＝，tan30°＝，，
∴min{sin30°，cs45°，tan30°}＝；
∵min{2，2x+2，4﹣2x}＝2，
∴，
∴0≤x≤1．
∴x的取值范围为0≤x≤1．
故答案为：；0≤x≤1；
（2）①M{2，x+1，2x}＝＝＝x+1，
∵M{2，x+1，2x}＝min{2，x+1，2x}，
∴min{2，x+1，2x}＝x+1，
∴，
∴x＝1．
故答案为：1；
②如果M{a，b，c}＝min{a，b，c}，那么a＝b＝c．理由：
若a≥c，b≥c，
∴min{a，b，c}＝c，
∵M{a，b，c}＝，M{a，b，c}＝min{a，b，c}，
∴＝c，
∴a+b﹣2c＝0，
∴（a﹣c）+（b﹣c）＝0，
∵a≥c，b≥c，
∴a﹣c≥0，b﹣c≥0，
∴a﹣c＝0，b﹣c＝0，
∴a＝b＝c．
当b≥a，c≥a或≥b，c≥b时，同样的方法可得：a＝b＝c．
故答案为：a＝b＝c；
③∵M{2x+y+2，x+2y，2x﹣y}＝min{2x+y+2，x+2y，2x﹣y}，
∴由（2）的结论可得：2x+y+2＝x+2y＝2x﹣y，
∴由2x+y+2＝x+2y得到：x﹣y＝﹣2，
由x+2y＝2x﹣y得到：x＝3y，
∴，
∴，
∴x+y＝﹣4．
故答案为：﹣4；
（3）在同一坐标系里画出函数y＝x+1，y＝（x﹣1）2，y＝2﹣x的图象，如图，
观察图象，min{x+1，（x﹣1）2，2﹣x}的最大值为1．
故答案为：1．
声明：试题解析著作权属所有，未经书面同意，不得复制发布2123
1D
2D
3B
4C
5C
6A
7B
8B
9D
10D
X(X+5)(X-5)
160
27/8
2＜k≤8
＜