上海市高桥中学2024-2025学年高三上学期期中考试数学试卷

这是一份上海市高桥中学2024-2025学年高三上学期期中考试数学试卷，共13页。试卷主要包含了11，; 2，C 14等内容，欢迎下载使用。
一、填空题（本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分）
1、若集合，，则________．
2、若复数，则其共轭复数的虚部为________．
3、已知角的顶点在坐标原点，始边与轴正半轴重合，若角的终边经过点，则________．
4、不等式的解集为________．
5、的展开式中，常数项为________．
6、双曲线的两条渐近线的夹角为________．
7、若对于任意的实数，恒成立，则实数的取值范围为________．
8、已知向量，的夹角为，且，，则________．
9、某电子设备有两套相互独立的供电系统和，在时间内系统和系统发生故障的概率为0.2和．若在时间内至少有一个系统不发生故障的概率为0.94，则________．
10、顶点为的圆锥的母线长为，底面半径为，，是底面圆周上的两点，为底面中心，且，则在圆锥侧面上由点到点的最短路线长
为________cm．（精确到）
11、对于正整数，记表示的最大奇数因数，例如，，．设．当，时，________．
12、已知函数，，若有且仅有一个正整数，使得不等式成立，则实数的取值范围为________．
二、选择题（本题满分18分，13-14题每题4分，15-16题每题5分）
13、用反证法证明“方程至多有两个解”的假设中，正确的是（ ）
A．至少有两个角 B．有且只有两个解
C．至少有三个解 D．至多有一个解
14、以下数据为某学校参加数学竞赛10人的成绩（单位：分）：72、86、80、88、83、78、81、90、91、92，则这10个成绩的第75百分位数是（ ）
A．90 B．89 C．88 D．88.5
15、已知抛物线，圆，过圆心作斜率为的直线与抛物线和圆交于四点，自上而下依次为，，，，若，则的值为（ ）
A． B． C． D．
16、已知函数的定义域为，定义集合，在使得的所有中，下列成立的是（ ）
A.存在，使得是偶函数
B.存在，使得在上单调递减
C.存在，使得在处取极大值
D.存在，使得是的最小值
三、解答题（本大题共有5分，满分78分）
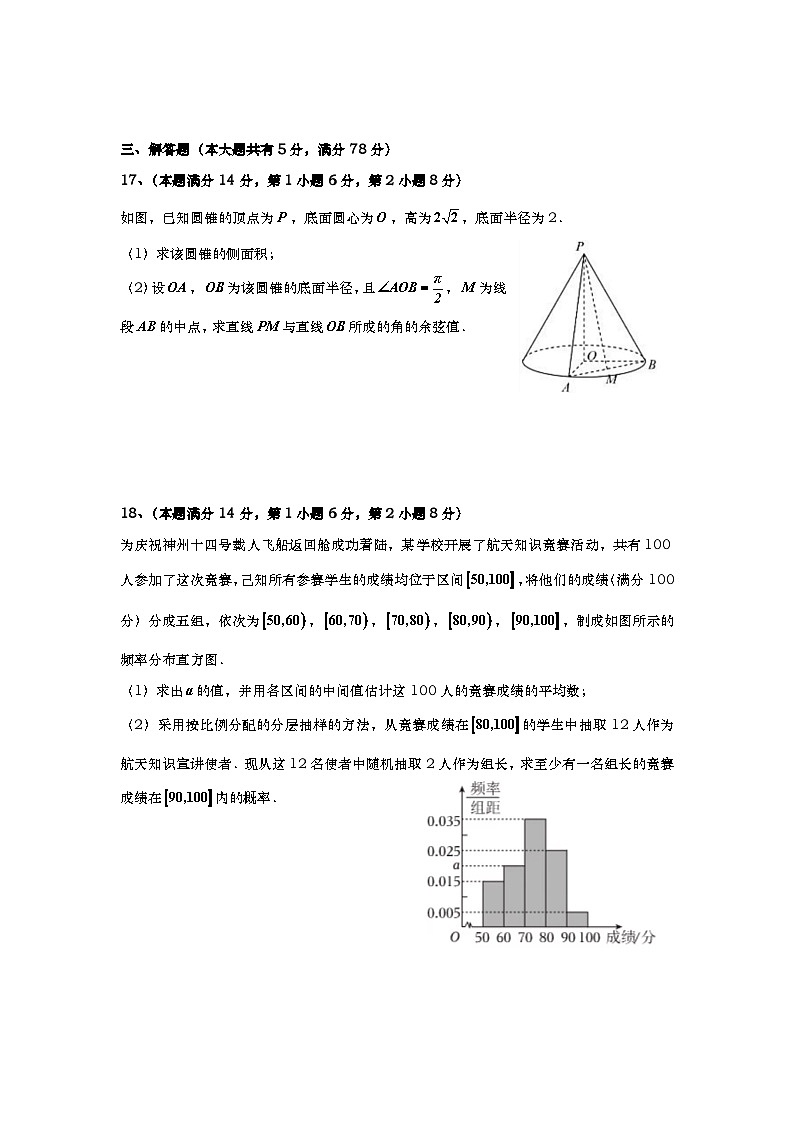
17、（本题满分14分，第1小题6分，第2小题8分）
如图，已知圆锥的顶点为，底面圆心为，高为，底面半径为2．
（1）求该圆锥的侧面积；
（2）设，为该圆锥的底面半径，且，为线段的中点，求直线与直线所成的角的余弦值．
18、（本题满分14分，第1小题6分，第2小题8分）
为庆祝神州十四号载人飞船返回舱成功着陆，某学校开展了航天知识竞赛活动，共有100人参加了这次竞赛，己知所有参赛学生的成绩均位于区间，将他们的成绩（满分100分）分成五组，依次为，，，，，制成如图所示的频率分布直方图．
（1）求出的值，并用各区间的中间值估计这100人的竞赛成绩的平均数；
（2）采用按比例分配的分层抽样的方法，从竞赛成绩在的学生中抽取12人作为航天知识宣讲使者．现从这12名使者中随机抽取2人作为组长，求至少有一名组长的竞赛成绩在内的概率．
19、（本题满分14分，第1小题6分，第2小题8分）
2023年杭州亚运会首次启用机器狗搬运赛场上的运动装备．如图所示，在某项运动赛事扇形场地中，，米，点是弧的中点，为线段上一点（不与点，重合）．为方便机器狗运输装备，现需在场地中铺设三条轨道，，记，三条轨道的总长度为米．
（1）将表示成的函数，并写出的取值范围；
（2）当三条轨道的总长度最小时，求轨道的长．
20、（本题满分18分，第1小题4分，第2小题6分，第3小题8分）
已知椭圆的焦距为，点在椭圆上，动直线与椭圆相交于不同的两点，，且直线，的斜率之积为1．
（1）求椭圆的标准方程；
（2）若直线的法向量为，求直线的方程；
（3）是否存在直线，使得为直角三角形?若存在，求出直线的斜率；若不存在，请说明理由．
21、（本题满分18分，第1小题4分，第2小题6分，第3小题8分）
若函数的图像上有两个不同点，处的切线重合，则称该切线为函数的图像的“自公切线”．
（1）试判断函数与的图像是否存在“自公切线”（不需要说明理由）；
（2）若，求函数的图像的“自公切线”方程；
（3）若，求证：函数，有唯一零点且该函数的图像不存在“自公切线”．
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.； 11. 12.
11、对于正整数，记表示的最大奇数因数，例如，，．设．当，时，________．
【答案】
【解析】当时，
于是.故答案为:.
12、已知函数，，若有且仅有一个正整数，使得不等式成立，则实数的取值范围为________．
【答案】
【解析】函数,当时，可得作图如下：
由题意,若,则,化简可得,解得,
当时,,此时不符合题意，
当时，令
令,且函数图象的对称轴为直线
由,则或,所以函数在上单调递减,
可得,则在上单调递减,
,则在上恒成立，所以此时不符合题意;
当时,可作图如下:显然不存在符合题意的.
综上所述，的取值范围为.故答案为:.
二、选择题
13.C 14. A 15. A 16.D
15、已知抛物线，圆，过圆心作斜率为的直线与抛物线和圆交于四点，自上而下依次为，，，，若，则的值为（ ）
A． B．
C． D．
【答案】A
【解析】如图,圆的圆心为,半径
显然点为抛物线的焦点,抛物线的准线方程为,
设则
所以,因此,即有,解得
设直线的方程为,显然,由
消去得,则有,解得.故选：B.
16、已知函数的定义域为，定义集合，在使得的所有中，下列成立的是（ ）
A.存在，使得是偶函数
B.存在，使得在上单调递减
C.存在，使得在处取极大值
D.存在，使得是的最小值
【答案】D
【解析】依题意，，
选项,若是偶函数,则,则当,时,
不满足选项错误.
选项,若在上单调递减,则,与题意矛盾，选项错误.
选项,若在处取极大值,则存在,使得在区间上,单调递增,
与""矛盾,所以选项错误.
选项,设,
画出图象如下图所示,
由图可知,满足,且是的最小值，所以选项正确.故选：D.
三．解答题
17.（1） （2）
18.（1）平均数为 （2）
19.（1） （2）
20、（本题满分18分，第1小题4分，第2小题6分，第3小题8分）
已知椭圆的焦距为，点在椭圆上，动直线与椭圆相交于不同的两点，，且直线，的斜率之积为1．
（1）求椭圆的标准方程；
（2）若直线的法向量为，求直线的方程；
（3）是否存在直线，使得为直角三角形?若存在，求出直线的斜率；若不存在，请说明理由．
【答案】（1） （2） （3）存在，直线的斜率为.
【解析】（1）由题意可得,可得,又因为
所以椭圆的方程为;
（2）由条件知:直线的斜率为,方程为
则由,得,所以,从而.
由于,所以直线的方程为,同理可得,
所以直线的斜率为,从而直线的方程为,
即.
（3）假设存在满足条件的直线,并设直线的方程为,
则由,得,所以,
由于,所以直线的方程为
同理可得,
故直线的斜率为
当为直角三角形时,只有可能,或,于是,或.
若,由,可得;从而;
若,由,可得，也有.因此,直线的斜率为.
21、（本题满分18分，第1小题4分，第2小题6分，第3小题8分）
若函数的图像上有两个不同点，处的切线重合，则称该切线为函数的图像的“自公切线”．
（1）试判断函数与的图像是否存在“自公切线”（不需要说明理由）；
（2）若，求函数的图像的“自公切线”方程；
（3）若，求证：函数，有唯一零点且该函数的图像不存在“自公切线”．
【答案】（1）存在,不存在; （2） （3）证明见解析
【解析】（1）因为直线是的图像的一条"自公切线",
故函数的图像存在"自公切线";
对于是严格减函数,
故在不同点处的切线斜率不同,所以函数的图像不存在"自公切线",
所以的图像存在"自公切线",函数的图像不存在"自公切线";
（2）函数,求导得
显然函数在上单调递增，函数在上单调递减，
设切点,则存在,使得,
则在点处的切线方程为,
在点处的切线方程为,
因此，消去可得
令,求导得
则函数在上单调递增,又,函数的零点为-1,
因此,所以曲线的"双重切线"的方程为.
（3）证明:因为,,
所以在上恒成立，且仅当时,
故是严格增函数，可得它至多有一个零点.
令,由的图像是连续曲线，
且所以在上存在零点,
故在上,存在零点,所以有唯一零点;
假设的图像存在"自公切线",则存在且,
使得的图像在与处的切线重合,故,
且,
由可得,不妨设,将代入,可得,
在上图的单位圆中,于,可知,
与矛盾.故的图像不存在"自公切线".