河南省商丘市夏邑县城北五乡联考2024-2025学年九年级上学期11月期中数学试题

这是一份河南省商丘市夏邑县城北五乡联考2024-2025学年九年级上学期11月期中数学试题，文件包含九年级数学期中测试docx、九年级数学期中测试参考答案docx等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
1．左下方是由8个棱长为1个单位长度的小立方体组成的立体图形（如图所示），从正面看这个立体图形得到的平面图形是（ ）
A．B．
C．D．
2．生活在数字时代的我们，很多场合都要用到二维码，二维码的生成原理是用特定的几何图形按编排规律在二维方向上分布，采用黑白相间的图形来记录数据符号信息．九年级学生丹丹帮妈妈打印了一个收款二维码如图所示，该二维码的面积为9cm2，他在该二维码纸内随机掷点，经过大量重复试验，发现点落在白色区域的频率稳定在0.6左右，则据此估计此二维码中黑色区域的面积为（ ）
A．3.6cm2B．4.5cm2C．5.4cm2D．9cm2
3．图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A、B、C都在横线上．若线段AB＝3，则线段AC的长是（ ）
A．1.5B．3C．4D．4.5
4．某果园今年栽种果树300棵，现计划扩大种植面积，使今后两年的栽种量都比前一年增长一个相同的百分数，这样三年（包括今年）的总栽种量为2100棵．若这个百分数为x．则由题意可列方程为（ ）
A．300（1+x）2＝2100
B．300+300（1+x）2＝2100
C．300（1+x）+300（1+x）2＝2100
D．300+300（1+x）+300（1+x）2＝2100
5．如图，在△ABC中，高BD，CE相交于点F，图中与△BEF相似的三角形共有（ ）
A．1个B．2个C．3个D．4个
6．数的图象经过点A（2，﹣4），则k的值为（ ）
A．B．C．8D．﹣8
7．如图，菱形ABCD中，点E，F，G分别为AB，AD，CD的中点，EF＝4，FG＝3，则菱形ABCD的周长为（ ）
A．12B．16C．18D．20
8．图，四边形OABC为矩形，点A，C分别在x轴和y轴上，连接AC，点B的坐标为（8，6），以A为圆心，任意长为半径画弧，分别交AC、AO于点M、N，再分别以M、N为圆心，大于长为半径画弧，两弧交于点Q，作射线AQ交y轴于点D，则点D的坐标为（ ）
A．（0，1）B．（0，2）C．D．
9．点B把线段AC分成两部分，如果＝＝k，那么k的值为（ ）
A．B．C．+1D．﹣1
10．某学校对教室采用药熏消毒，已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例，药物燃烧完后，y与x成反比例（如图），现测得药物10分钟燃毕，此时室内空气中每立方米含药量为8毫克．研究表明，当空气中每立方米的含药量不低于4毫克才有效，那么此次消毒的有效时间是（ ）
A．11分钟B．12分钟C．15分钟D．20分钟
二．填空题（共5小题，满分15分，每小题3分）
11．如果，则＝ ．
12．一元二次方程x2﹣8x+6＝0根的判别式的值为 ．
13．《九章算术》第九章“勾股”问题十九：“今有邑方（正方形小城）不知大小，各开中门．出北门三十步有木，出西门七百五十步见木．问：邑方几何（小城的边长）？”根据描述如图所示，其中E表示西门，F表示北门，G处是木（E，F分别是所在边的中点）．则邑的边长为 步．
14．如图，在等腰直角三角形ABC中，若AB＝2，则S△ABC＝ ．
15．如图，△ABC中，AB＝4，BC＝5，AC＝6，点D、E分别是AC、AB边上的动点，折叠△ADE得到△A′DE，且点A′落在BC边上，若△A′DC恰好与△ABC相似，AD的长为 ．
三．解答题（共8小题，满分75分）
16．（10分）解方程：
（1）x2﹣x﹣3＝0；
（2）x2+7x＝24+2x．
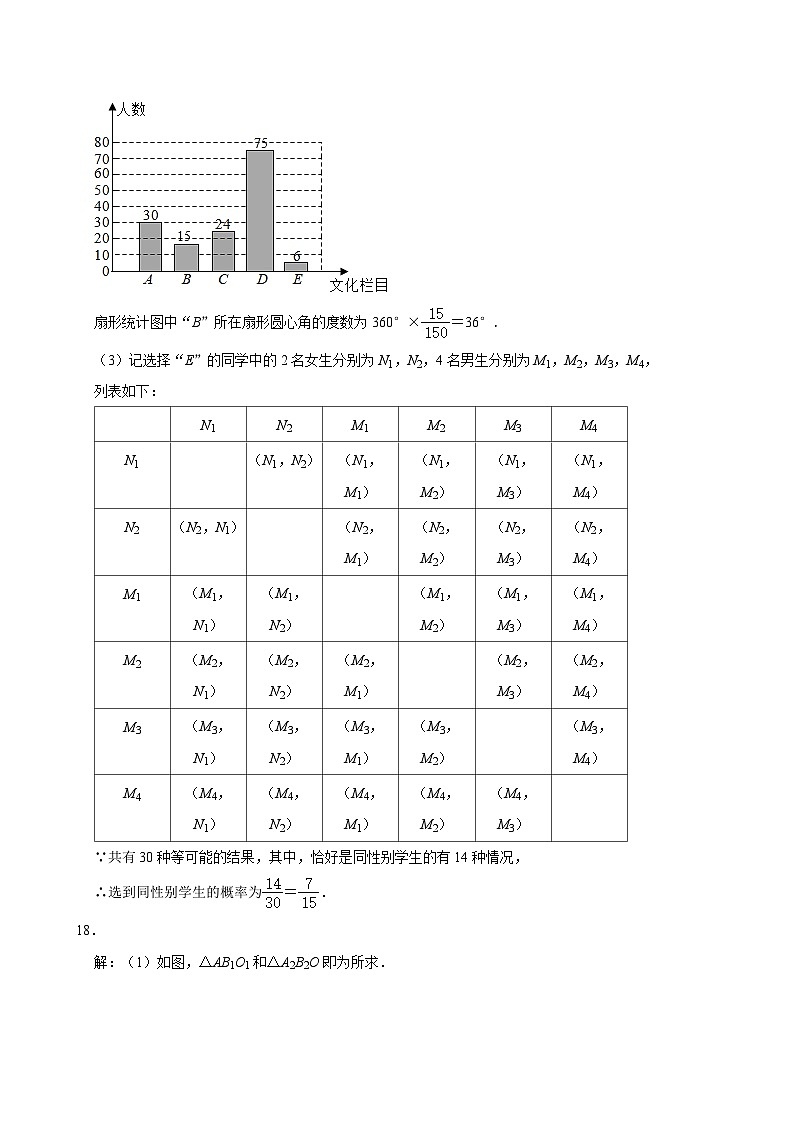
17．（9分）为推进特色学校创建工作，丰富通学生们的体育活动，某校决定成立篮球、乒乓球、排球、足球、羽毛球社团，为了解学生对这些项目的喜爱情况，学校体育组老师随机抽取了部分学生进行调查，被调查的学生只能从篮球（记为A）、乒乓球（记为B）、排球（记为C）、足球（记为D）、羽毛球（记为E）选择一项．根据调查结果绘制成如图所示的两幅不完整的统计图．
请根据图中信息解答下列问题：
（1）在这项调查中，共调查了多少名学生？
（2）将条形统计图补充完整，并求出扇形统计图中“B”所在扇形圆心角的度数；
（3）若选择“E”的学生中有2名女生，其余为男生，现从选择“E”的学生中随机选出两名学生参加表演赛，请直接写出选到同性别学生的概率．
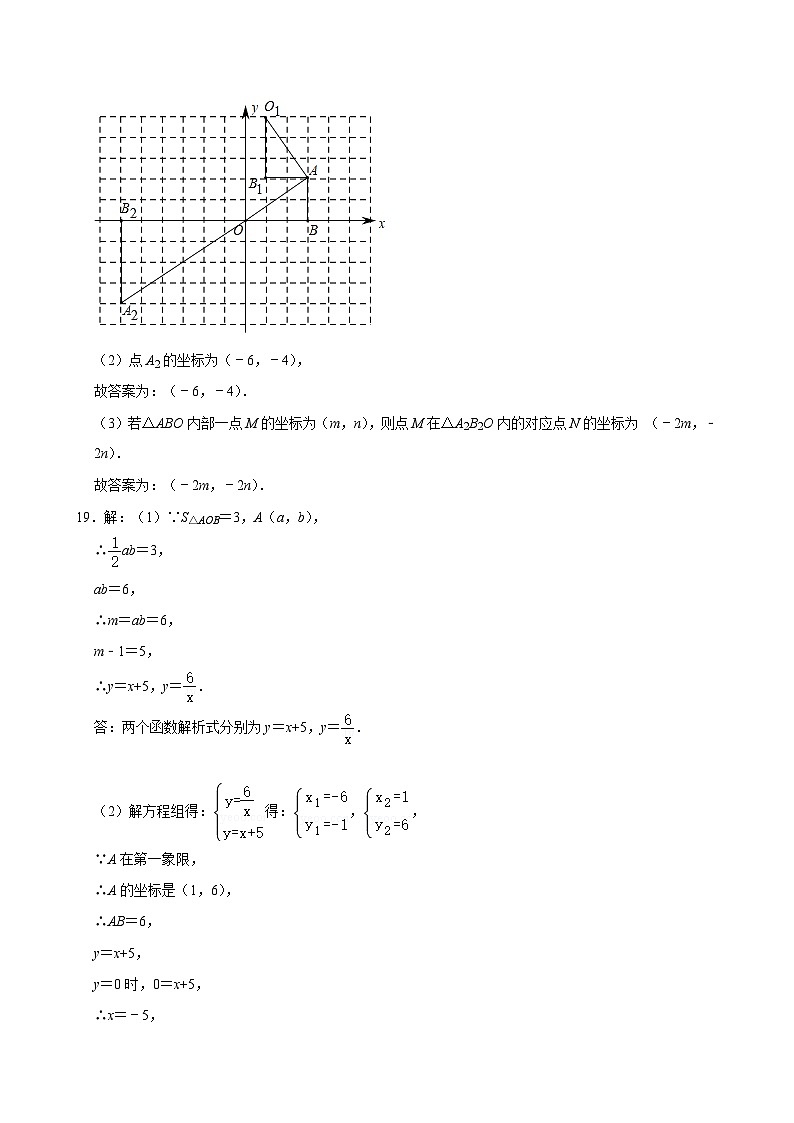
18．（9分）如图，点A的坐标为（3，2），点B的坐标为（3，0）作如下操作：
①以点A为旋转中心，将△ABO顺时针方向旋转90°，得到△AB1O1；
②以点O为位似中心，将△ABO放大，得到△A2B2O，使相似比为1：2，且点A2在第三象限．
（1）在图中画出△AB1O1和△A2B2O；
（2）点A2的坐标为 ；
（3）若△ABO内部一点M的坐标为（m，n），则点M在△A2B2O内的对应点N的坐标为 ．
19．（9分）已知函数y＝x+m﹣1与交于第一象限一点A（a，b），AB⊥x轴于B，S△AOB＝3．
（1）求两个函数解析式；
（2）求△ABC的面积．
20．（9分）如图，某城建部门计划在新建的城市广场的一块长方形空地上修建一个面积为1200m2的停车场，将停车场四周余下的空地修建成同样宽的通道，已知整个长方形空地的长为50m，宽为40m．
（1）求四周通道的宽度；
（2）某建筑公司希望用80万元的承包金额承揽这项工程，城建部门认为金额太高需要降价，经过两次协商，最终以51.2万元达成一致，若两次降价的百分率相同，求每次降价的百分率．
21．（9分）位于陕西省北部神木县红碱淖景区的大门口，树立着一座精致的王昭君雕像．在当地人看来，当年王昭君就是走过神木大地，去完成和亲使命的．她因为远离家乡而伤心落泪，泪水也因此化作了一颗“沙漠明珠”——红碱淖．某校社会实践小组为了测量这座雕像（如图1）的高度，如图2，小明先在地面上C处垂直于地面竖立了高度为2米的标杆CD，这时地面上的点E，标杆的顶端点D，雕像的顶端B正好在同一直线上，测得EC＝3米；小明再从点E出发沿着EG方向前进9米，到达点F．在点F处放置一平面镜，小刚站在G处时，恰好在平面镜中看到雕像的顶端B的像，此时测得小刚的眼睛到地面的距离GH为1.5米，GF＝3米．已知点G、F、E、C与雕像的底端A在同一直线上，AB⊥AG，CD⊥AG，GH⊥AG，请你根据以上数据，计算该雕像的高度AB．（平面镜大小忽略不计）
22．（10分）（1）观察猜想
如图1，点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE＝90°，AD＝AE，则BC、BD、CE之间的数量关系为 ，请说明理由（证明过程）．
（2）拓展延伸
如图2，在四边形ABCD中，∠ABC＝∠ADC＝90°，CB＝5，AB＝2，DC＝DA，请直接写出BD的长．
（3）问题解决
如图3，在Rt△ABC中，∠ABC＝90°，CB＝4，AB＝2，以AC为直角边作等腰△DAC，且∠CAD＝90°连结BD，则BD的长为 ．
23．（10分）如图，在Rt△ABC中，∠ACB＝90°，，AC＝2，点D在边AB上运动，连结CD．过点A作AE⊥CD，交边BC于点E，交线段CD于点F．
（1）边BC的长为 ；
（2）当△ACF与△ABC相似时，求AD的长；
（3）运动过程中，当点B、F的距离最小时，求这个最小值及此时△ACF的面积；
（4）连结DE，当四边形ACED为轴对称图形时，直接写出BD的长．