

浙江省温州市2023_2024学年高一数学上学期阶段性测试12月月考试题含解析
展开
这是一份浙江省温州市2023_2024学年高一数学上学期阶段性测试12月月考试题含解析,共19页。试卷主要包含了 命题“”的否定是, 若,,则“”是“”的, 已知函数y=f, ,,,则, 已知函数是奇函数,则实数, 若,,则的最小值为, 已知函数等内容,欢迎下载使用。
A. B.
C. D.
【答案】A
【解析】
【分析】利用全称命题的否定方法求解,改变量词,否定结论.
【详解】因为的否定为,
所以选A.
【点睛】本题主要考查含有量词的命题的否定,一般处理策略是:先改变量词,然后否定结论.
2. 若,,则“”是“”的()
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【答案】D
【解析】
【分析】利用对数函数定义域的求法与二次不等式化简集合,再利用充分必要条件的定义即可得解.
【详解】因为,
当时,取,则由,得,解得,
此时,此时不成立,故充分性不成立;
当时,取,由,得,解得,
此时,满足,但不成立,故必要性不成立;
综上,“”是“”的既不充分也不必要条件.
故选:D.
3. 已知扇形的圆心角为2弧度,且圆心角所对的弦长为4,则该扇形的面积为()
A. B. C. D.
【答案】A
【解析】
【分析】由扇形的弧长和面积公式求解即可.
【详解】因为扇形的圆心角弧度为2,所对弦长为4,为圆心,如下图,
取的中点,连接,则,则,
则扇形的半径,所以扇形的弧长,
则扇形的面积为.
故选:A.
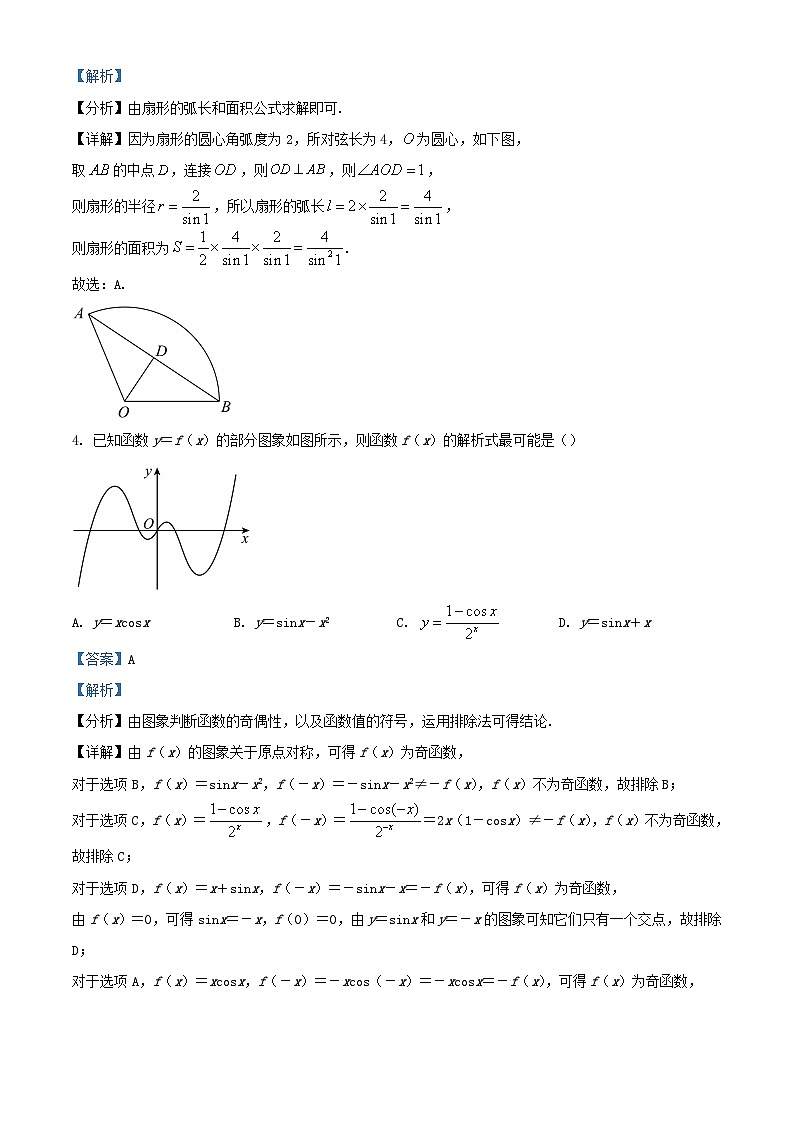
4. 已知函数y=f(x)的部分图象如图所示,则函数f(x)的解析式最可能是()
A. y=xcsxB. y=sinx-x2C. D. y=sinx+x
【答案】A
【解析】
【分析】由图象判断函数的奇偶性,以及函数值的符号,运用排除法可得结论.
【详解】由f(x)的图象关于原点对称,可得f(x)为奇函数,
对于选项B,f(x)=sinx-x2,f(-x)=-sinx-x2≠-f(x),f(x)不为奇函数,故排除B;
对于选项C,f(x)=,f(-x)==2x(1-csx)≠-f(x),f(x)不为奇函数,故排除C;
对于选项D,f(x)=x+sinx,f(-x)=-sinx-x=-f(x),可得f(x)为奇函数,
由f(x)=0,可得sinx=-x,f(0)=0,由y=sinx和y=-x的图象可知它们只有一个交点,故排除D;
对于选项A,f(x)=xcsx,f(-x)=-xcs(-x)=-xcsx=-f(x),可得f(x)为奇函数,
且f(x)=0时,x=0或x=kπ+(k∈Z),f()<0,f(π)<0,
故选项A最可能正确.
故选:A.
5. ,,,则()
A. B. C. D.
【答案】B
【解析】
【分析】根据对数函数和指数函数的单调性即可得出,,的大小关系.
【详解】,
,,
.
故选:.
6. 已知函数是奇函数,则实数()
A. B. C. 1D. 2
【答案】D
【解析】
【分析】根据函数为奇函数的性质,可进行求解.
【详解】由题知为奇函数,所以得:,
即:,解之得:,故D项正确.
故选:D
7. 若函数有4个零点,则正数的取值范围是()
A. B. C. D.
【答案】B
【解析】
【分析】根据一次函数与对数函数的图象,得到时,函数只有一个零点,结合题意,得到时,方程有三个零点,利用三角函数的性质,得出不等式,即可求解.
【详解】当时,令,即,即,
因为函数与的图象仅有一个公共点,如图所示,
所以时,函数只有一个零点,
又由函数有4个零点,
所以时,方程有三个零点,如图所示,
因为,可得,则满足,
解得,即实数的取值范围为.
故选:B.
8. 若,,则的最小值为()
A. 4B. C. 8D.
【答案】C
【解析】
【分析】首先变形,再两次利用基本不等式,即可求最值.
【详解】,
其中,其中,
当时,即时,等号成立,
,当,即时等号成立,
当满足,即,时,两个等号同时成立,
所以的最小值为8.
故选:C
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 下列函数中,在区间上为增函数的是()
A. B.
C. D.
【答案】AB
【解析】
【分析】根据指数函数的单调性可判断选项A;根据图象的变换及对数函数的单调性可判断选项B;先去绝对值,再根据二次函数的单调性可判断选项C;根据正切函数的单调性可判断选项D.
【详解】对于选项A:因为函数在上单调递增,且,
所以在区间上单调递增,故选项A正确;
对于选项B:因为函数的图象是由函数的图象向右平移1个单位得到的,而函数在上单调递增;所以函数在上单调递增,故选项B正确;
对于选项C:当时,.
由二次函数的单调性可得:函数在上单调递减,故选项C正确;
对于选项D:由正切函数的性质可知函数在上单调递增.
因为,所以选项D错误.
故选:AB.
10. 已知函数(,,)在处取得最小值,与此最小值点相邻的的一个零点为,则()
A. B.
C. 是奇函数D. 在上单调递减
【答案】AC
【解析】
【分析】由结合题意与余弦型函数的性质可得的解析式,可得A、B;再借助解析式对C、D逐一验证即可.
【详解】由最小值为,,可得,
由在处取得最小值,且与此最小值点相邻的一个零点为,
故,即,又,则,
有,解得,
又,则,即,
故A正确、B错误;
,
由为奇函数,故为奇函数,即C正确;
若,则,
而不是的单调递减区间,
故不是的单调递减区间,
故D错误.
故选:AC.
11. 设,为正数,且,则( )
A. B. C. D.
【答案】ACD
【解析】
【分析】通过变形为,,即可判定选项A,B;利用基本不等式构造的不等关系式即可判定选项C;利用消元求出的最值,从而得到,将代入,即可判定选项D.
【详解】因为,所以,且,
因为a,b为正数,所以,,即,,故A正确,B错误;
因,所以同除可得,
又a,b为正数,可得,
当且仅当时取得等号,则,
故,所以,故C正确;
因为,所以,又,所以,
所以,
当且仅当,即时取得等号,即,
因为,所以,
所以,即,故D正确.
故选:ACD.
12. 记区间M=[a,b],集合N={y|y=,x∈M},若满足M=N成立的实数对(a,b)有且只有1个,则实数k可以取()
A. ﹣2B. C. 1D. 3
【答案】AD
【解析】
【分析】分类讨论,对a,b的取值情况分类考虑,由集合与函数的性质进行分析,即可求出满足题意的k.
【详解】∵y=,当x=0时,y=0,
当x≠0时,y=,可知函数为偶函数,
若存在唯一实数对(a,b)使M=N,
若,,,,即,此时 ,
若,不合题意,若,则,此时区间内含有0,
由x=0时,y=0时知,此时必有 ,或,矛盾;
所以综上述只有当x=a时,y=b,当x=b时,y=a,
即,两式相乘得,
∴k2=(|a|+1)(|b|+1)或k2=﹣(|a|+1)(|b|+1),
∵k2>0,
∴k2=(|a|+1)(|b|+1),
又∵|a|>0,
∴|a|+1>1,同理|b|+1>1,
∴(|a|+1)(|b|+1)>1,
即k2>1,
k>1或k<﹣1,
故满足条件为AD,
故选:AD.
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知,则______.
【答案】
【解析】
【分析】求出即可得出的值.
【详解】由题意,
在中,
,
∴,
故答案为:.
14. 已知函数的图象不经过第二、四象限,请写出满足条件的一组的值________.
【答案】(答案不唯一)
【解析】
【分析】根据给定条件,可得函数的图象过原点求出,再按分类讨论即得.
【详解】函数的定义域为,当,即时,的图象必过第四象限,矛盾,
因此,由函数的图象不经过第二、四象限,得点只能在原点,
则,即,当时,若,则有,的图象必过第四象限,矛盾,
当时,若,则,此时的图象在第三象限,
若,则,此时的图象在第一象限,
所以且,满足条件的一组的值可以为.
故答案为:
15. 已知,,则______.
【答案】
【解析】
【分析】利用换元法与三角函数的基本关系式,结合诱导公式与倍角公式即可得解.
【详解】因为,令,则,,
又,所以,则,
所以,故,
.
故答案为:.
16. 理论上,一张纸经过一定次数对折之后厚度能超过地月距离,但实际上,因为纸张本身有厚度,我们并不能将纸张无限次对折,当我们的厚度超过纸张的长边时,便不能继续对折了.一张长边为,厚度为的矩形纸张沿两个方向不断对折,则经过两次对折,长边变为,厚度变为.在理想情况下,对折次数有下列关系:,根据以上信息,一张长为30,厚度为0.05的纸张最多能对折的次数为___________.
【答案】
【解析】
【分析】解不等式来求得次数.
【详解】依题意
,
,
所以,即,
所以正整数的最大值为.
故答案为:
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 设集合,,.
(1)若,求;
(2)若,求实数的取值范围.
【答案】17.
18.
【解析】
【分析】(1)解对数不等式与二次方程化简集合,从而得解;
(2)分类讨论与,结合二次方程根的分布即可得解.
【小问1详解】
由,得,
解得,则,
当时,可化为,
解得或,则,
所以.
【小问2详解】
因为,所以,
当时,由,得,解得;
当时,令,其开口向上,对称轴为,
则,即,解得;
综上,,即的取值范围为.
18. 已知().
(1)若为偶函数,求的值;
(2)若的最小值为,求的对称中心.
【答案】18.
19.
【解析】
【分析】(1)由偶函数定义列式结合三角函数运算得解;
(2)将化简,由的最小值为,可求得,再由正弦函数的性质得解.
【小问1详解】
因为是偶函数,所以,即,化简得,
或,
解得,,又,
所以.
【小问2详解】
由
,由的最小值为,
则,即,又,
所以,
所以,由可知,
令,,即,
所以的对称中心为,.
19. 设函数,满足:①;②对任意,恒成立.
(1)求函数的解析式.
(2)设矩形的一边在轴上,顶点,在函数的图象上.设矩形的面积为,求证:.
【答案】(1);
(2)证明见解析
【解析】
【分析】(1)利用待定系数法,结合题设条件即可得解;
(2)先利用导数判断的图象性质,从而利用矩形面积公式得到关于的表达式,从而得证.
【小问1详解】
因为,
由,得,则;
由,得,恒成立,
即恒成立,所以,所以,
所以;
【小问2详解】
因为,
令,得;令,得;
所以在单调递增,单调递减.
不妨设,,由知,
那么,;
故,
因为,所以.
20. 已知函数为偶函数.
(1)求实数的值;
(2)若关于的不等式恒成立,求实数的取值范围;
(3)设函数的零点为,求证:.
【答案】(1)
(2)
(3)证明见解析
【解析】
【分析】(1)根据偶函数的定义求得的值.
(2)利用分离常数法,结合换元法、函数的单调性来求得的取值范围.
(3)先求得的取值范围,结合函数的单调性证得不等式成立.
【小问1详解】
,
由于为偶函数,
所以,即,
所以,.
【小问2详解】
依题意关于的不等式恒成立,
即,
,
令,当时等号成立,
由于是单调递增函数,,即,
所以.
【小问3详解】
函数的零点为,
即,
函数在上递增,,
,
所以,
对任意,
,
其中,所以,即在上递增,
所以,
即.
21. 在月亮和太阳的引力作用下,海水水面发生的周期性涨落现象叫做潮汐.一般早潮叫潮,晚潮叫汐.受潮汐影响,港口的水深也会相应发生变化.下图记录了某港口某一天整点时刻的水深y(单位:米)与时间x(单位:时)的大致关系:
假设4月份的每一天水深与时间的关系都符合上图所示.
(1)请运用函数模型,根据以上数据写出水深y与时间x的函数的近似表达式;
(2)根据该港口的安全条例,要求船底与水底的距离必须不小于3.5米,否则该船必须立即离港.一艘船满载货物,吃水(即船底到水面的距离)6米,计划明天进港卸货.
①求该船可以进港的时间段;
②该船今天会到达港口附近,明天0点可以及时进港并立即开始卸货,已知卸货时吃水深度以每小时0.3米的速度匀速减少,卸完货后空船吃水3米.请设计一个卸货方案,在保证严格遵守该港口安全条例的前提下,使该船明天尽早完成卸货(不计停靠码头和驶离码头所需时间).
【答案】(1);
(2)①0点到4点以及12点到16点进入港口;②该船在0点进港开始卸货,5点暂时驶离港口,11点返回港口继续卸货,16点完成卸货任务.
【解析】
【分析】(1)根据给定的图形,求出函数模型中的各个参数作答.
(2)①根据给定条件,列出不等式求解作答;②求出最小水深的函数关系,数形结合求解作答.
【小问1详解】
观察图形知,,解得,,,解得,
显然函数的图象过点,即,又,因此,
所以函数表达式为.
【小问2详解】
①依题意,,整理得,
即有,即,
解得或,
所以该船可以在0点到4点以及12点到16点进入港口.
②由①结论知,该船明日0点即可进港开始卸货,
设自0点起卸货小时后,该船符合安全条例的最小水深为,
如图,函数与的图像交于点,
即卸货5小时后,在5点该船必须暂时驶离港口,此时该船的吃水深度为4.5米,
令,即,,
解得,显然,
该船在11点可返回港口继续卸货,5小时后完成卸货,此时为16点,
综上所述,方案如下:该船在0点进港开始卸货,5点暂时驶离港口,11点返回港口继续卸货,16点完成卸货任务.
【点睛】思路点睛:给定的部分图象求解解析式,一般是由函数图象的最高(低)点定A,求出周期定,由图象上特殊点求.
22. 设函数,,其中.
(1)当时,求函数值域;
(2)记的最大值为M,
①求M;
②求证:.
【答案】(1);(2)①;②证明见解析.
【解析】
分析】
(1)化简得,配方求值域即可;
(2)①设,换元得,分类讨论即可求解;②利用绝对值不等式的性质求出利用做差法与比较大小即可求证.
【详解】(1)
当时,
因为,
所以
(2)设,,
对称轴为,开口向上,,,
1)当时,,,所以
2)当时,,,所以
3)当时,,,所以
综上所述:
②
当时,
所以
当时,
所以
当时,,所以
综上所述:所以
【点睛】关键点点睛:证明时,先求出的最大值是解题关键,应用绝对值不等式的性质,可求出,然后分类利用作差法比较大小即可,属于难题.
相关试卷
这是一份浙江省温州市2023_2024学年高一数学上学期期中联考试题含解析,共22页。试卷主要包含了考试结束后,只需上交答题纸, 如果,那么, 设,,则等内容,欢迎下载使用。
这是一份浙江省温州市2023_2024学年高二数学上学期12月月考试题含解析,共21页。试卷主要包含了 直线的倾斜角是, 抛物线的焦点到准线的距离, 定义“等方差数列”, 若,则, 已知,下列说法正确的是等内容,欢迎下载使用。
这是一份浙江省金华市2023_2024学年高一数学上学期12月月考试题含解析,共20页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。








