雅礼集团2024年初二上学期期中考试数学试题（原卷）

这是一份雅礼集团2024年初二上学期期中考试数学试题（原卷），共4页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
命题人：杨景华、戴雄燕审题人：王先志
考生注意：本试卷共3道大题，25道小题，满分120分，时量120分钟.
一、单项选择题(本大题共10个小题，每小题3分，共30分)
1. “致中和，天地位焉，万物育焉.”对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光. 下面四幅图是我国传统文化与艺术中的几个经典图案，其中不是轴对称图形的是 ( )
2.已知一个三角形的两边长分别为3和4，则第三边长不可能是 ( )
A. 1 B. 2 C. 3 D. 4
3.下列各式运算正确的是 ( )
A.x²⋅x³=x⁶ B.x²³=x⁶ C.x²+x³=x⁵ D.x⁶÷x³=x²
4.如图, 在△ABC中, ∠A=35°, ∠B=60° , 则∠C的度数为( )
A. 65° B. 75°
C. 85° D. 95°
5.如图, AC、BD相交于O, ∠1=∠2, 若直接用“SAS”说明△ABC≌△BAD, 则还需加上条件 ( )
A. AD=BC B. ∠D=∠C
C. OA=AB D. AC=BD
6.若点M(a, -3) 与点N(2, -3) 关于y轴对称, 则a=( )
A. 2 B. -2 C. 3 D. -3
7.已知等腰三角形的两边长分别为6和3，则此等腰三角形的周长为 ( )
A. 9 B. 12 C. 15 D. 12或15
8.如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在 ( )
A.三边高线的交点处 B.三边中线的交点处
C.三内角平分线的交点处 D.三边垂直平分线的交点处
9.已知(x+m)(x+3)的展开式中不含 x的一次项, 则m的值为 ( )
A. -3 B. 3 C. 0 D. 1
10.如图, AD是等腰Rt△ABC的角平分线, ∠ACB=90°,AC=BC,过点B作BE//AC, 且BE=CD, 连接CE交AD于点F, 交AB于点P,点M是线段AF上的动点，点N是线段AP 上的动点，连接PM、MN，下列五个结论: ① AD=CE;②AD⊥CE;③BE=BP;④CD+AC=AB;
circle5PM+MN≥12AB,其中正确的有 ( ).
A.2个 B.3个 C.4个 D.5个
1二、填空题(本大题共6个小题，每小题3分，共18分)
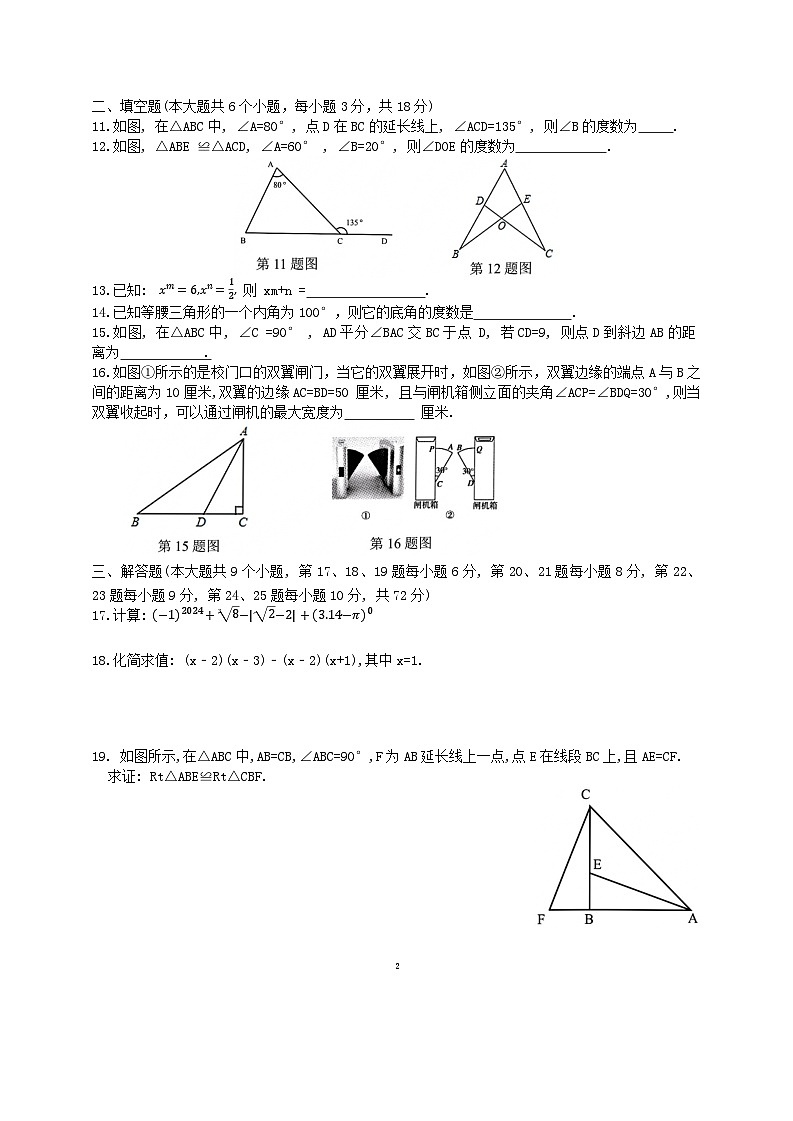
11.如图, 在△ABC中, ∠A=80°, 点D在BC的延长线上, ∠ACD=135°, 则∠B的度数为 .
12.如图, △ABE ≌△ACD, ∠A=60° , ∠B=20°, 则∠DOE的度数为 .
13.已知: xm=6,xn=12, 则 xm+n = .
14.已知等腰三角形的一个内角为100°，则它的底角的度数是 .
15.如图, 在△ABC中, ∠C =90° , AD平分∠BAC交BC于点 D, 若CD=9, 则点D到斜边AB的距离为 .
16.如图①所示的是校门口的双翼闸门，当它的双翼展开时，如图②所示，双翼边缘的端点A与B之间的距离为10厘米,双翼的边缘AC=BD=50 厘米, 且与闸机箱侧立面的夹角∠ACP=∠BDQ=30°,则当双翼收起时，可以通过闸机的最大宽度为 厘米.
三、解答题(本大题共9个小题, 第17、18、19题每小题6分, 第20、21题每小题8分, 第22、23题每小题9分, 第24、25题每小题10分, 共72分)
17.计算: −12024+38−|2−2|+3.14−π0
18.化简求值: (x﹣2)(x﹣3)﹣(x﹣2)(x+1),其中x=1.
19. 如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在线段BC上,且AE=CF. 求证: Rt△ABE≌Rt△CBF.
220.如图, △ABC的三个顶点的坐标分别是A(-2,3)、B(-2,1)、C(1,-2).
(1) 点A、B、C关于x轴对称的点分别为A₁、B₁、C₁, 在图中作出△ABC 关于x轴对称的. △A₁B₁C₁;
(2) 直接写出点C关于直线l(直线l上各点的横坐标都为2) 对称的点( C₂的坐标；
(3) 求△ABC 的面积.
21. 在计算 (2x+a)(x+b) 时, 甲错把 a 看成了-a, 得到结果是: 2x²−10x+12; 乙由于漏抄了第一个多项式中x的系数，得到结果： x²+x−12.
(1) 求出a, b的值;
(2) 在 (1) 的条件下, 计算 (2x+a)(x+b) 的结果.
22.如图所示, AB=AC, ∠ABD=∠ACE, ∠BAC=∠DAE,
(1) 求证: △ABD≌△ACE;
(2) 若∠CAE=20° , ∠ACE=25° , 求∠ADE的度数;
(3) 在 (2) 的条件下判断△ADE的形状, 并证明.
23.已知: 如图, 在△ABC中, AB=BC, ∠B=120° .
(1)用直尺和圆规作出AB的垂直平分线，分别交AC、AB于点M、N(保留作图痕迹，不写作法)；
(2) 猜想CM与AM之间有何数量关系，并证明你的猜想；
(3) 在直线MN上找一点P,使PB+PC之和最小, 若AM=2, 求I PB+PC的最小值.
324.已知: 在△ABC中, ∠ACB=90° , AC=BC=4.
(1) 如图1, BD是△ABC的中线.
①△BCD 的面积是 ;
②已知: CF⊥BD, 交AB于点E, AF⊥AC,连接DE, 求证: ∠BDC=∠EDA;
(2)如图2, 点 M为线段CA 延长线上一点, 过点 A作AQ⊥AB,过点M作BM的垂线交 AQ于点P,线段PA的延长线与线段BC的延长线交于点N，是否存在点M，使 SΔAMP=32SΔAMN,若存在，求CM的长； 若不存在，请说明理由.
25. 平面直角坐标系中，如果一个点到两坐标轴距离相等，则该点称为“雅点”，例如(1，1)、(2，-2)、 (-3, -3)、 (4, -4) 都称为“雅点”.
(1)如图1，点A(6，0)，则线段OA的垂直平分线l上的第一象限的“雅点”D的坐标为 .
(2) 若n为正整数, 点M(x⁴n, 4)是“雅点”，求 x³ⁿ²−4x²5n的值；
(3) 如图2,△AOM和△OFT都是等边三角形, 点M、O、F在一条直线上, 点A (4, 0), 连接AF交y轴于点K,连接MT交AF于点H,点Q为y轴上一点,连接AQ,MQ,AQ与OM交于点P,当H为第四象限的“雅点”时, ∠QPO=∠OKF, 求点Q的坐标。
4