吉林省吉林市 舒兰市第十六中学校2023-2024学年上学期八年级期中测试数学卷

这是一份吉林省吉林市 舒兰市第十六中学校2023-2024学年上学期八年级期中测试数学卷，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
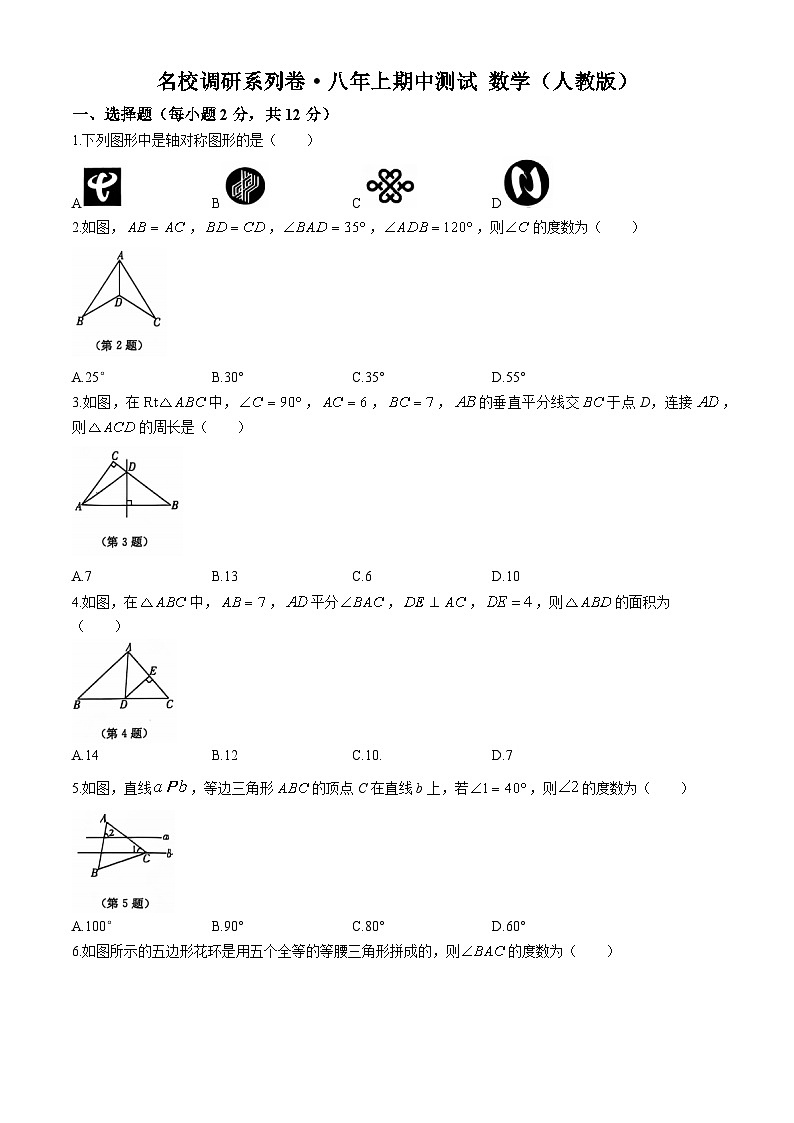
1.下列图形中是轴对称图形的是（ ）
ABCD
2.如图，，，，，则的度数为（ ）
A.25°B.30°C.35°D.55°
3.如图，在中，，，，的垂直平分线交于点D，连接，则的周长是（ ）
A.7B.13C.6D.10
4.如图，在中，，平分，，，则的面积为（ ）
A.14B.12C.10.D.7
5.如图，直线，等边三角形的顶点C在直线b上，若，则的度数为（ ）
A.100°B.90°C.80°D.60°
6.如图所示的五边形花环是用五个全等的等腰三角形拼成的，则的度数为（ ）
A.28°B.36°C.45°D.72°
二、填空题（每小题3分，共24分）
7.已知点，则点M关于x轴对称的点的坐标是______.
8.2024年初，山西省最长的跨黄河大桥——临猗黄河大桥完成合龙任务，如图是桥身的一部分，桥身采用三角形钢结构架，这其中蕴含的数学道理是______.
9.若等边三角形的边长是，则的周长是______.
10.如图，已知在和中，，，，若用“”判定，则需要添加的条件是______.
11.如图，，，，，则______.
12.如图，P是等边三角形内一点，，______°.
13.如图，在中，，，点D在上，，，则______.
14.如图，已知，，若和分别垂直平分和，则______°.
三、解答题（每小题5分，共20分）
15.如图，与相交于点O，连接、，，，求证：.
16.若一个n边形的内角和的比它的外角和少150°，求n的值.
17.如图，是的外角的平分线，且交的延长线于点E，若，.求的度数.
18.如图，在边长为1的正方形组成的网格中，的顶点均在格点上，点A、B的坐标分别为、.
（1）画出关于y轴成轴对称的，点A的对应点为点，并写出点的坐标；
（2）求的面积.
四、解答题（每小题7分，共28分）
19.如图，在四边形中，，的平分线与的延长线交于点E，，求证：是等边三角形.
20.已知三角形的三条边长分别为7、15和x.
（1）x的取值范围为______；
（2）当该三角形为等腰三角形时，求它的周长.
21.图①、图②均是的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点A、B、C、D均在格点上.只用无刻度的直尺按下列要求在给定的网格中画图，所画图形的顶点均在格点上，不要求写画法.
（1）在图①中，以线段为边画一个轴对称三角形，使其面积为3；
（2）在图②中，以为边画一个四边形，使其是轴对称图形.
22.如图，在中，，点D、E、F分别在、、边上，且，.
（1）求证：是等腰三角形；
（2）当时，求的度数.
五、解答题（每小题8分，共16分）
23.如图，在中，的垂直平分线交于点E，交于点F，D为线段的中点，.
（1）求证：；
（2）若，求的度数.
24.如图，是等边三角形，过点B作于点D，过点D作，且，连接.
（1）求证：是等边三角形；
（2）若，求的周长.
六、解答题（每小题10分，共20分）
25.已知为等边三角形，点D在边上.
【基本图形】如图①，以为一边作等边三角形，连接.可得（无需证明）；
【迁移运用】如图②，点F是边上一点，以为一边作等边三角形，连接，过点D作，交于点G.求证：；
【类比探究】如图③，点F是边的延长线上一点，以为一边作等边三角形，过点D作，交于点H，连接，写出线段、、之间的数量关系并说明理由.
26.如图，在中，，，点D为边的中点.动点P从点B出发，以每秒2个单位长度的速度沿射线运动，同时动点Q从点C出发，以每秒个单位长度的速度沿线段向终点A运动，设点P运动的时间为t秒.
（1）用含t的代数式表示线段的长并写出t的取值范围；
（2）当，且为等腰三角形时，求的度数；
（3）当，且点P在边上时，若与全等，直接写出a和t的值.
名校调研系列卷·八年上期中测试数学（人教版）
参考答案
一、1.C 2.A 3.B 4.A 5.C 6.B
二、7.（3，5） 8.三角形具有稳定性 9.36 10. 11.4 12.120 13.12 14.90
三、15.证明：在与中，.
16.解：.
17.解：.
18.解：（1）如图，即为所求，点的坐标为.
（2）3.5.
四、19.证明：，，的平分线与的延长线交于点E，，，，是等边三角形.
20.解：（1）.
（2）37.
21.解：（1）如图①.
（2）如图②.
22.（1）证明：，，在和中，，是等腰三角形.
（2）解：.
五、23.（1）证明：连接，是的垂直平分线，，，，D为线段的中点，.
（2）解：.
24.解：（1）证明：是等边三角形，，，，又，是等边三角形.
（2）解：6.
六、25.【迁移运用】证明：是等边三角形，，，，，是等边三角形，，是等边三角形，，，，即，在与中，，，.
【类比探究】解：，理由如下：是等边三角形，，，，，是等边三角形，，是等边三角形，，，，即，在与中，，，，.
26.解：（1）当时，；当时，.
（2）当点P在线段上时，若，则；若，则，；若，则，；点P在线段的延长线上，当时，则，，.
综上的度数为70°或40°或55°或35°.
（3），或，.