

所属成套资源:2024-2025学年上学期初中数学北师大版八年级期中必刷常考题
2024-2025学年上学期初中数学北师大版八年级期中必刷常考题之平面直角坐标系
展开
这是一份2024-2025学年上学期初中数学北师大版八年级期中必刷常考题之平面直角坐标系,共13页。
A.(5,3)B.(﹣5,3)或(5,3)
C.(3,5)D.(﹣3,5)或(3,5)
2.(2024春•北海期末)在平面直角坐标系中,点(﹣3,4)在( )
A.第一象限B.第二象限C.第三象限D.第四象限
3.(2023秋•西安期末)已知点P在第四象限内,到x轴的距离等于3,到y轴的距离等于4,则点P坐标是( )
A.(3,﹣4)B.(3,4)C.(﹣4,3)D.(4,﹣3)
4.(2023秋•海曙区校级期末)已知A(2,a),B(b,﹣3)是平面直角坐标系上的两个点,AB∥x轴,且点B在点A的右侧.若AB=5,则( )
A.a=﹣3,b=﹣3B.a=﹣3,b=7C.a=2,b=2D.a=﹣8,b=2
5.(2023秋•姜堰区期末)在平面直角坐标系中,点P(m2+2024,﹣1)一定在( )
A.第一象限B.第二象限C.第三象限D.第四象限
二.填空题(共5小题)
6.(2023秋•阿荣旗期末)平面直角坐标系内一点P(﹣2,3)关于原点对称的点的坐标是 .
7.(2024春•阳信县期末)已知点P(2a﹣6,a+1),若点P在坐标轴上,则点P的坐标为 .
8.(2023秋•白银区期末)点P是第二象限内的点,且P到x轴的距离是4,到y轴的距离是3,则点P的坐标是 .
9.(2023秋•黑龙江期末)在平面直角坐标系中,已知点A(2,m)和点B(n,﹣1)关于x轴对称,则m+n的值是 .
10.(2023秋•志丹县期末)点(﹣3,5)关于原点对称的点的坐标是 .
三.解答题(共5小题)
11.(2023秋•新民市期末)如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 ;
(2)若点D与点C关于原点对称,则点D的坐标为 ;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
12.(2024春•金平区期中)已知点P(2a﹣2,a+5),解答下列各题.
(1)点Q的坐标为(4,5),直线PQ∥y轴;求出点P的坐标;
(2)若点P在第二象限,且它到x轴、y轴的距离相等,求a2023的值.
13.(2024春•高安市期中)在平面直角坐标系中,已知点M(m﹣2,2m﹣7),点N(n,3).
(1)若M在x轴上,求m的值;
(2)若点M到x轴,y轴距离相等,求m的值;
(3)若MN∥y轴,点M在点N的上方且MN=2,求n的值.
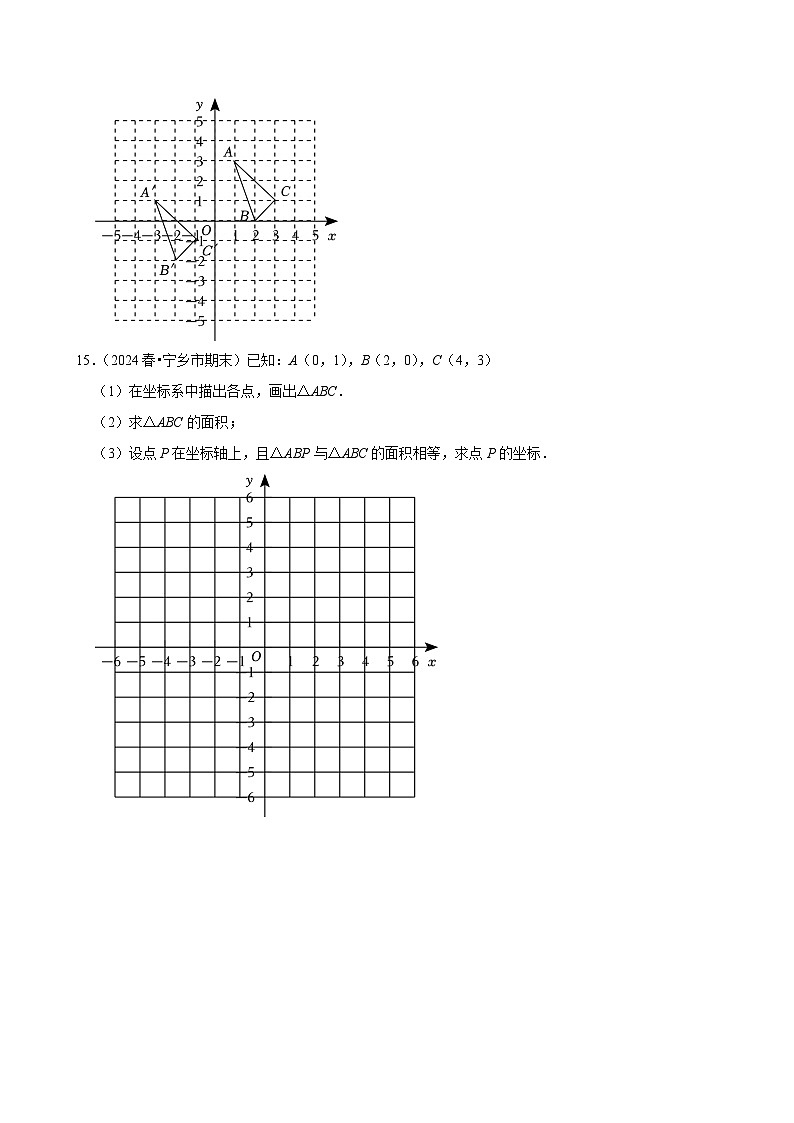
14.(2024春•右玉县期末)△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ;B ;C ;
(2)若点P(x,y)是△ABC内部一点,则△A′B′C′内部的对应点P′的坐标为 .
15.(2024春•宁乡市期末)已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
2024-2025学年上学期初中数学北师大版八年级期中必刷常考题之平面直角坐标系
参考答案与试题解析
一.选择题(共5小题)
1.(2024春•应城市期末)点M在x轴的上方,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,3)B.(﹣5,3)或(5,3)
C.(3,5)D.(﹣3,5)或(3,5)
【考点】点的坐标.
【专题】推理能力.
【答案】D
【分析】要根据两个条件解答:
①M到y轴的距离为3,即横坐标为±3;
②点M距离x轴5个单位长度,x轴上方,即M点纵坐标为5.
【解答】解:∵点距离x轴5个单位长度,
∴点M的纵坐标是±5,
又∵这点在x轴上方,
∴点M的纵坐标是5;
∵点距离y轴3个单位长度即横坐标是±3,
∴M点的坐标为(﹣3,5)或(3,5).
故选:D.
【点评】本题主要考查了点的坐标的几何意义,横坐标的绝对值就是到y轴的距离,纵坐标的绝对值就是到x轴的距离.
2.(2024春•北海期末)在平面直角坐标系中,点(﹣3,4)在( )
A.第一象限B.第二象限C.第三象限D.第四象限
【考点】点的坐标.
【答案】B
【分析】根据各象限内点的坐标特征解答.
【解答】解:点(﹣3,4)在第二象限.
故选:B.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
3.(2023秋•西安期末)已知点P在第四象限内,到x轴的距离等于3,到y轴的距离等于4,则点P坐标是( )
A.(3,﹣4)B.(3,4)C.(﹣4,3)D.(4,﹣3)
【考点】点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】D
【分析】先判断出点P的横纵坐标的符号,进而根据到坐标轴的距离判断点的具体坐标.
【解答】解:∵点P在第四象限内,
∴点P的横坐标大于0,纵坐标小于0,
∵点P到x轴的距离是3,到y轴的距离是4,
∴点P的横坐标是4,纵坐标是﹣3,即点P的坐标为(4,﹣3).
故选:D.
【点评】本题主要考查了点的坐标的几何意义,横坐标的绝对值就是到y轴的距离,纵坐标的绝对值就是到x轴的距离.
4.(2023秋•海曙区校级期末)已知A(2,a),B(b,﹣3)是平面直角坐标系上的两个点,AB∥x轴,且点B在点A的右侧.若AB=5,则( )
A.a=﹣3,b=﹣3B.a=﹣3,b=7C.a=2,b=2D.a=﹣8,b=2
【考点】坐标与图形性质.
【专题】平面直角坐标系;运算能力.
【答案】B
【分析】由A与B的坐标,根据AB与x轴平行,确定出a的值,根据AB=5求出b的值即可.
【解答】解:∵A(2,a),B(b,﹣3),且AB=5,且AB∥x轴,
∴a=﹣3,b﹣2=5,
解得:a=﹣3,b=7,
故选:B.
【点评】此题考查了坐标与图形性质,熟练掌握运算法则是解本题的关键.
5.(2023秋•姜堰区期末)在平面直角坐标系中,点P(m2+2024,﹣1)一定在( )
A.第一象限B.第二象限C.第三象限D.第四象限
【考点】点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】D
【分析】根据各象限内点的坐标特征解答即可.
【解答】解:∵m2≥0,
∴m2+2024>0,
∴在平面直角坐标系中,点P(m2+2024,﹣1)一定在第四象限.
故选:D.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
二.填空题(共5小题)
6.(2023秋•阿荣旗期末)平面直角坐标系内一点P(﹣2,3)关于原点对称的点的坐标是 (2,﹣3) .
【考点】关于原点对称的点的坐标.
【专题】平面直角坐标系;应用意识.
【答案】见试题解答内容
【分析】平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),从而可得出答案.
【解答】解:根据中心对称的性质,得点P(﹣2,3)关于原点对称点P′的坐标是(2,﹣3),
故答案为:(2,﹣3).
【点评】本题主要考查关于原点对称的点坐标的关系,是需要识记的基本问题.记忆方法是结合平面直角坐标系的图形记忆.
7.(2024春•阳信县期末)已知点P(2a﹣6,a+1),若点P在坐标轴上,则点P的坐标为 (﹣8,0)或(0,4) .
【考点】点的坐标.
【答案】见试题解答内容
【分析】分点P在x轴上,纵坐标为0;在y轴上,横坐标为0,分别列式求出a的值,再求解即可.
【解答】解:当P在x轴上时,a+1=0,解得a=﹣1,P(﹣8,0);
当P在y轴上时,2a﹣6=0,解得a=3,P(0,4).
所以P(﹣8,0)或(0,4).
故答案为(﹣8,0)或(0,4).
【点评】本题考查了点的坐标,主要是对坐标轴上的点的坐标特征的考查,易错点在于要分情况讨论.
8.(2023秋•白银区期末)点P是第二象限内的点,且P到x轴的距离是4,到y轴的距离是3,则点P的坐标是 (﹣3,4) .
【考点】点的坐标.
【专题】平面直角坐标系;几何直观.
【答案】(﹣3,4).
【分析】根据点到x轴的距离是纵坐标的绝对值,点到y轴的距离是横坐标的绝对值,结合第二象限内点的坐标特征可得出答案.
【解答】解:∵点P在第二象限,且P到x轴的距离是4,到y轴的距离是3,
∴点P的横坐标为﹣3,纵坐标为4,
∴点P的坐标为(﹣3,4).
故答案为:(﹣3,4).
【点评】本题考查点的坐标,利用点到x轴的距离是纵坐标的绝对值,点到y轴的距离是横坐标的绝对值是解题的关键.
9.(2023秋•黑龙江期末)在平面直角坐标系中,已知点A(2,m)和点B(n,﹣1)关于x轴对称,则m+n的值是 3 .
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;推理能力.
【答案】见试题解答内容
【分析】根据关于x轴对称的点的坐标特点求出m、n的值,然后代入代数式进行计算即可得解.
【解答】解:∵A(2,m)和B(n,﹣1)关于x轴对称,
∴n=2,m=1,
∴m+n=2+1=3.
故答案为:3.
【点评】本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
10.(2023秋•志丹县期末)点(﹣3,5)关于原点对称的点的坐标是 (3,﹣5) .
【考点】关于原点对称的点的坐标.
【答案】见试题解答内容
【分析】根据关于原点对称的点的横坐标与纵坐标都互为相反数解答.
【解答】解:点(﹣3,5)关于原点对称的点的坐标是(3,﹣5).
故答案为:(3,﹣5).
【点评】本题考查了关于原点对称的点的坐标,熟记两点关于原点对称,则两点的横、纵坐标都是互为相反数是解题的关键.
三.解答题(共5小题)
11.(2023秋•新民市期末)如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 4 ;
(2)若点D与点C关于原点对称,则点D的坐标为 (﹣4,﹣3) ;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
【考点】关于原点对称的点的坐标;三角形的面积.
【专题】平面直角坐标系;运算能力.
【答案】(1)4;
(2)(﹣4,﹣3);
(3)(10,0)或(﹣6,0).
【分析】(1)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(2)利用关于原点对称点的性质得出答案;
(3)利用三角形面积求法得出符合题意的答案.
【解答】解:(1)如图所示:△ABC的面积是:3×4−12×1×2−12×2×4−12×2×3=4;
故答案为:4;
(2)点D与点C关于原点对称,则点D的坐标为:(﹣4,﹣3);
故答案为:(﹣4,﹣3);
(3)∵P为x轴上一点,△ABP的面积为4,
∴BP=8,
∴点P的横坐标为:2+8=10或2﹣8=﹣6,
故P点坐标为:(10,0)或(﹣6,0).
【点评】此题主要考查了三角形面积求法以及关于y轴对称点的性质,正确得出对应点位置是解题关键.
12.(2024春•金平区期中)已知点P(2a﹣2,a+5),解答下列各题.
(1)点Q的坐标为(4,5),直线PQ∥y轴;求出点P的坐标;
(2)若点P在第二象限,且它到x轴、y轴的距离相等,求a2023的值.
【考点】坐标与图形性质.
【专题】平面直角坐标系;运算能力.
【答案】见试题解答内容
【分析】(1)根据平行于y轴的直线的横坐标相等,可得关于a的方程,解得a的值,再求得其纵坐标即可得出答案;
(2)根据第二象限的点的横纵坐标的符号特点及它到x轴、y轴的距离相等,可得关于a的方程,解得a的值,再代入要求的式子计算即可.
【解答】解:(1)点Q的坐标为(4,5),直线PQ∥y轴,
∴2a﹣2=4,
∴a=3,
∴a+5=8,
∴点P的坐标为(4,8);
(2)∵点P在第二象限,且它到x轴、y轴的距离相等,
∴2a﹣2=﹣(a+5),
∴2a﹣2+a+5=0,
∴a=﹣1,
∴a2023=﹣1.
【点评】本题考查了坐标与图形的性质,熟练掌握平面直角坐标系中的点的坐标特点是解题的关键.
13.(2024春•高安市期中)在平面直角坐标系中,已知点M(m﹣2,2m﹣7),点N(n,3).
(1)若M在x轴上,求m的值;
(2)若点M到x轴,y轴距离相等,求m的值;
(3)若MN∥y轴,点M在点N的上方且MN=2,求n的值.
【考点】坐标与图形性质.
【专题】平面直角坐标系;几何直观;运算能力.
【答案】(1)m=72;
(2)m=5或m=3;
(3)n的值为4.
【分析】(1)根据点M在x轴上,其纵坐标等于0得到2m﹣7=0,解答即可;
(2)根据点M到x轴,y轴距离相等,其横坐标的绝对值等于纵坐标的绝对值得到|m﹣2|=|2m﹣7|,解答即可;
(3)根据平行y轴,点M与点N的横坐标相等,得到m=4或m=6,即可解答.
【解答】解:(1)∵点M(m﹣2,2m﹣7)在x轴上,
∴2m﹣7=0,
解得:m=72;
(2)∵点M(m﹣2,2m﹣7)到x轴,y轴距离相等,
∴|m﹣2|=|2m﹣7|,
即m﹣2=2m﹣7或m﹣2=7﹣2m,
解得:m=5或m=3;
(3)∵MN∥y,且MN=2,
∴点M(m﹣2,2m﹣7),点N(n,3),
∴|2m﹣7﹣3|=2,n=m﹣2,
解得:m=4或m=6,
当m=4时,n=4﹣2=2(舍去),
当m=6时,n=6﹣2=4,
综上,n的值为4.
【点评】本题考查了坐标与图象性质,掌握平面直角坐标系中点在坐标轴的特点是解题的关键.
14.(2024春•右玉县期末)△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A (1,3) ;B (2,0) ;C (3,1) ;
(2)若点P(x,y)是△ABC内部一点,则△A′B′C′内部的对应点P′的坐标为 (x﹣4,y﹣2) .
【考点】坐标与图形性质.
【专题】平面直角坐标系;运算能力.
【答案】(1)(1,3);(2,0);(3,1);
(2)(x﹣4,y﹣2).
【分析】(1)根据点的位置写出坐标即可;
(2)利用平移变换的规律进行分析即可得到答案.
【解答】解:(1)由图可得:A(1,3),B(2,0),C(3,1),
故答案为:(1,3);(2,0);(3,1);
(2)解:由图可知,A(1,3),A′(﹣3,1),
将△ABC向左平移4个单位,再向下平移2个单位得到△A′B′C′,
∵点P(x,y)是△ABC内部一点,
∴△A′B′C′内部的对应点P′的坐标为(x﹣4,y﹣2),
故答案为:(x﹣4,y﹣2).
【点评】本题考查了图形的平移,坐标与图形,点的平移变换的规律:左减右加,上加下减.
15.(2024春•宁乡市期末)已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
【考点】坐标与图形性质;三角形的面积.
【答案】见试题解答内容
【分析】(1)确定出点A、B、C的位置,连接AC、CB、AB即可;
(2)过点C向x、y轴作垂线,垂足为D、E,△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积;
(3)当点p在x轴上时,由△ABP的面积=4,求得:BP=8,故此点P的坐标为(10,0)或(﹣6,0);当点P在y轴上时,△ABP的面积=4,解得:AP=4.所以点P的坐标为(0,5)或(0,﹣3).
【解答】解:(1)如图所示:
(2)过点C向x、y轴作垂线,垂足为D、E.
∴四边形DOEC的面积=3×4=12,△BCD的面积=12×2×3=3,△ACE的面积=12×2×4=4,△AOB的面积=12×2×1=1.
∴△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积
=12﹣3﹣4﹣1=4.
(3)当点p在x轴上时,△ABP的面积=12AO⋅BP=4,即:12×1×BP=4,解得:BP=8,
所以点P的坐标为(10,0)或(﹣6,0);
当点P在y轴上时,△ABP的面积=12×BO×AP=4,即12×2×AP=4,解得:AP=4.
所以点P的坐标为(0,5)或(0,﹣3).
所以点P的坐标为(0,5)或(0,﹣3)或(10,0)或(﹣6,0).
【点评】本题主要考查的是点的坐标与图形的性质,明确△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积是解题的关键.
相关试卷
这是一份2024-2025学年上学期初中数学北师大版八年级期中必刷常考题之轴对称与坐标变化,共22页。试卷主要包含了关于 轴对称,2022的值为 等内容,欢迎下载使用。
这是一份2024-2025学年上学期初中数学北师大版八年级期中必刷常考题之探索勾股定理,共15页。
这是一份2024-2025学年上学期初中数学北师大版八年级期中必刷常考题之数的开方,共10页。试卷主要包含了若2+b−2=0,则,8的立方根是 等内容,欢迎下载使用。










