宁夏省固原市泾源县2024年九上数学开学学业质量监测模拟试题【含答案】

这是一份宁夏省固原市泾源县2024年九上数学开学学业质量监测模拟试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）完成以下任务，适合用抽样调查的是（ ）
A．调查你班同学的年龄情况
B．为订购校服，了解学生衣服的尺寸
C．对北斗导航卫星上的零部件进行检查
D．考察一批炮弹的杀伤半径．
2、（4分）分式有意义的条件是（ ）
A．B．C．D．
3、（4分）下列变形中，正确的是（ ）
A．B．
C．D．
4、（4分）武汉某中学体育特长生的年龄，经统计有12、13、14、15四种年龄，统计结果如图.根据图中信息可以判断该批队员的年龄的众数和中位数为( )
A．8和6B．15和14C．8和14D．15和13.5
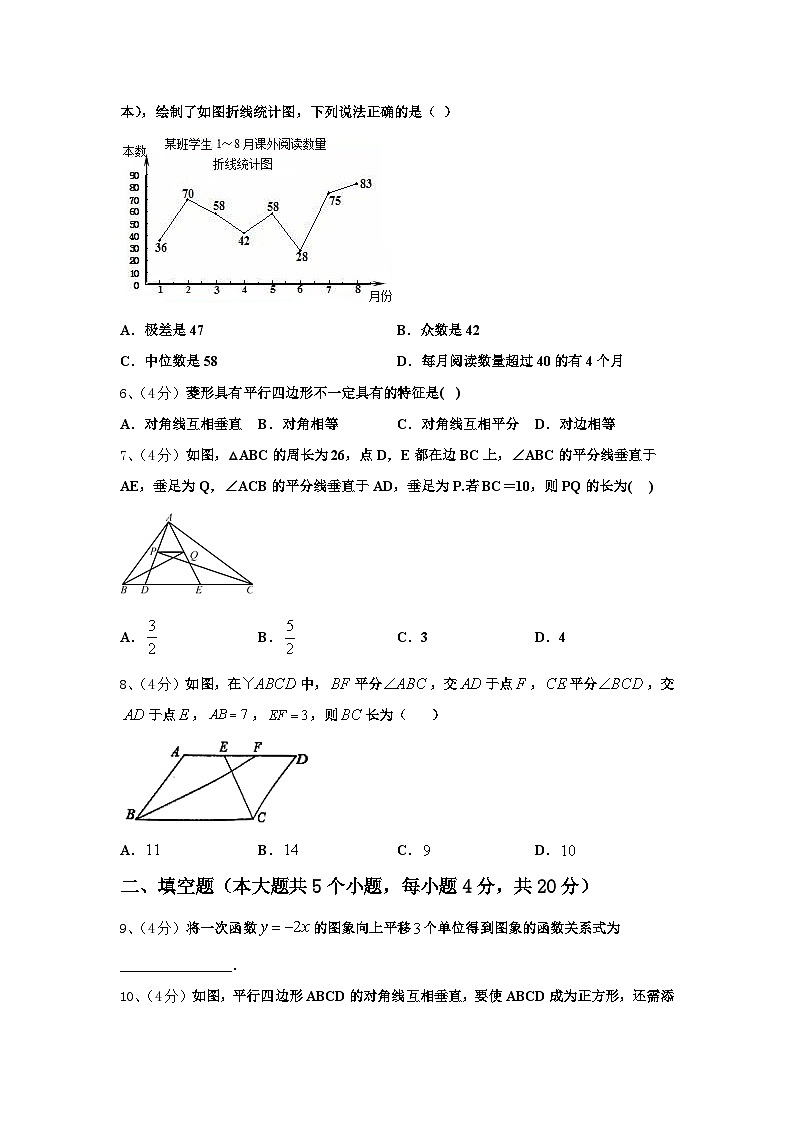
5、（4分）多多班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图折线统计图，下列说法正确的是（ ）
A．极差是47B．众数是42
C．中位数是58D．每月阅读数量超过40的有4个月
6、（4分）菱形具有平行四边形不一定具有的特征是( )
A．对角线互相垂直B．对角相等C．对角线互相平分D．对边相等
7、（4分）如图，△ABC的周长为26，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P.若BC＝10，则PQ的长为( )
A．B．C．3D．4
8、（4分）如图，在中，平分，交于点，平分，交于点，，，则长为（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）将一次函数的图象向上平移个单位得到图象的函数关系式为________________．
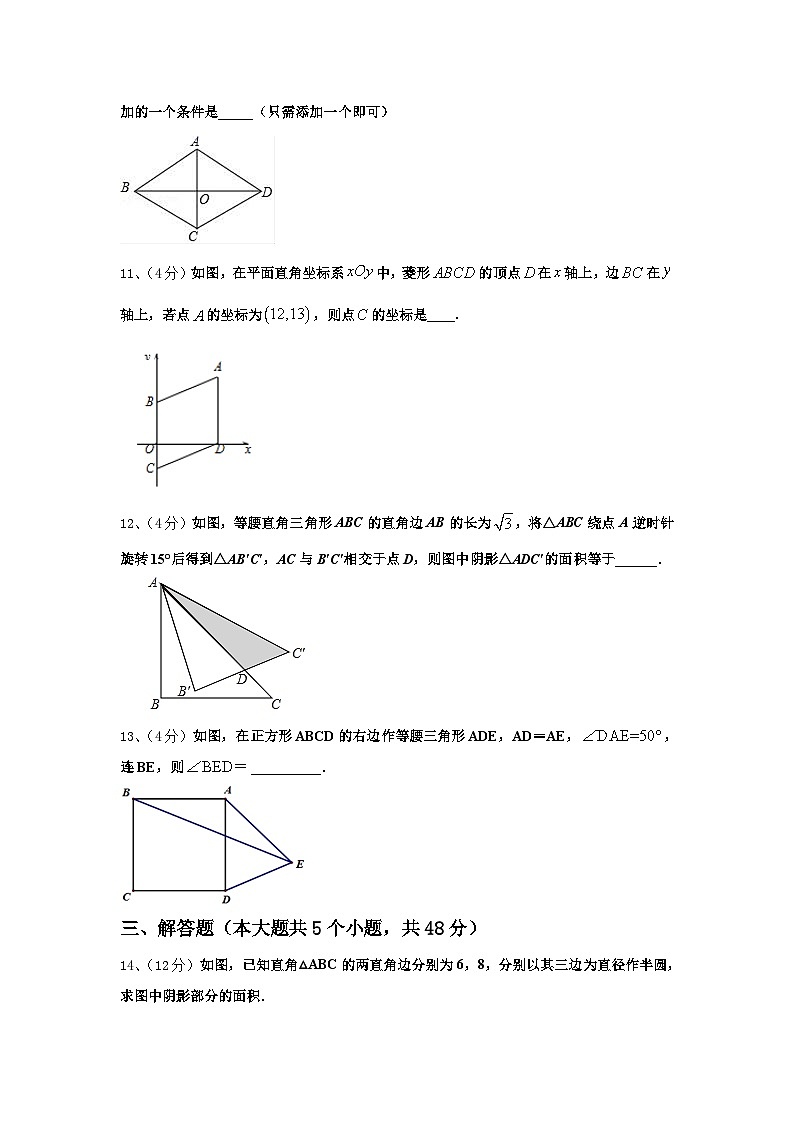
10、（4分）如图，平行四边形ABCD的对角线互相垂直，要使ABCD成为正方形，还需添加的一个条件是_____（只需添加一个即可）
11、（4分）如图，在平面直角坐标系中，菱形的顶点在轴上，边在轴上，若点的坐标为，则点的坐标是____.
12、（4分）如图，等腰直角三角形ABC的直角边AB的长为，将△ABC绕点A逆时针旋转15°后得到△AB′C′，AC与B′C′相交于点D，则图中阴影△ADC′的面积等于______．
13、（4分）如图，在正方形ABCD的右边作等腰三角形ADE，AD＝AE，，连BE，则__________．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，已知直角△ABC的两直角边分别为6，8，分别以其三边为直径作半圆，求图中阴影部分的面积．
15、（8分）如图，矩形中，，将矩形绕点旋转得到矩形，使点的对应点落在上，交于点，在上取点，使．
（1）求证：；
（2）求的度数；
（3）若，求的长．
16、（8分）如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B．
（1）求A，B两点的坐标；
（2）过B点作直线BP与x轴相交于P，且使OP=2OA， 求直线BP的解析式.
17、（10分）（1）如图1，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开；再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN，MN．请你观察图1，猜想∠MBN的度数是多少，并证明你的结论；
（2）将图1中的三角形纸片BMN剪下，如图2，折叠该纸片，猜测MN与BM的数量关系，无需证明．
18、（10分）对于平面直角坐标系xOy中的点P和正方形给出如下定义:若正方形的对角线交于点O，四条边分别和坐标轴平行，我们称该正方形为原点正方形，当原点正方形上存在点Q，满足PQ≤1时，称点P为原点正方形的友好点.
(1)当原点正方形边长为4时，
①在点P1(0，0)，P2(-1，1)，P3(3，2)中，原点正方形的友好点是__________；
②点P在直线y=x的图象上，若点P为原点正方形的友好点，求点P横坐标的取值范围；
(2)乙次函数y=-x+2的图象分别与x轴，y轴交于点A，B，若线段AB上存在原点正方形的友好点，直接写出原点正方形边长a的取值范围.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）已知关于x的分式方程有一个正数解，则k的取值范围为________.
20、（4分）若正多边形的一个内角等于150°，则这个正多边形的边数是______．
21、（4分）已知，，，，，……（即当为大于1的奇数时，；当为大于1的偶数时，），按此规律，____________．
22、（4分）如图，函数y=kx+b（k≠0）的图象经过点（1，2），则不等式kx+b＞2的解集为______．
23、（4分）如图，将绕点按逆时针方向旋转得到，使点落在上，若，则的大小是______°.
二、解答题（本大题共3个小题，共30分）
24、（8分）（1）发现．①；②；③；……写出④ ；⑤ ；
（2）归纳与猜想．如果n为正整数，用含n的式子表示这个运算规律；
（3）证明这个猜想．
25、（10分）某市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨2元收费．如果超过20吨，未超过的部分仍按每吨2元收费，超过部分按每吨2.5元收费．设某户每月用水量为x吨，应收水费为y元．
（1）分别写出当每月用水量未超过20吨和超过20吨时，y与x之间的函数关系式；
（2）若某用户5月份和6月份共用水45吨，且5月份的用水量不足20吨，两个月共交水费95元，求该用户5月份和6月份分别用水多少吨？
26、（12分）如图，已知函数y＝x+1和y＝ax+3的图象交于点P，点P的横坐标为1，
（1）关于x，y的方程组 的解是 ；
（2）a＝ ；
（3）求出函数y＝x+1和y＝ax+3的图象与x轴围成的几何图形的面积．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来，具体问题具体分析，普查结果准确，所以在要求精确、难度相对不大，实验无破坏性的情况下应选择普查方式，当考查的对象很多或考查会给被调查对象带来损伤破坏，以及考查经费和时间都非常有限时，普查就受到限制，这时就应选择抽样调查．
【详解】
解：A、人数不多，容易调查，宜采用全面调查；
B、为订购校服，了解学生衣服的尺寸是要求精确度高的调查，适合全面调查；
C、对北斗导航卫星上的零部件进行检查，因为调查的对象比较重要，应采用全面调查；
D、考察一批炮弹的杀伤半径适合抽样调查；
故选D．
本题主要考查了全面调查和抽样调查，解题时根据调查的对象的范围的大小作出判断，当范围较小时常常采用全面调查．
2、C
【解析】
根据分式有意义的定义即可得出答案.
【详解】
∵分式有意义
∴x-2≠0，即x≠2
故答案选择C.
本题考查的是分式有意义，比较简单，分式有意义即分母不等于0.
3、A
【解析】
分式的基本性质是分式的分子、分母同时乘以或除以同一个非1的数或式子，分式的值不变．而如果分式的分子、分母同时加上或减去同一个非1的数或式子，分式的值改变．
【详解】
A、，正确；
B、，错误；
C、，错误；
D、，错误；
故选A．
本题主要考查了分式的性质．注意约分是约去分子、分母的公因式，并且分子与分母相同时约分结果应是1，而不是1．
4、B
【解析】
根据众数和中位数的定义解答即可．
【详解】
解：15岁的队员最多，是8人，所以众数是15岁，20人中按照年龄从小到大排列，第10、11两人的年龄都是14岁，所以中位数是14岁．
故选B．
本题为统计题，考查众数与中位数的意义，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．
5、C
【解析】
根据统计图可得出最大值和最小值，即可求得极差；出现次数最多的数据是众数；将这8个数按大小顺序排列，中间两个数的平均数为中位数；每月阅读数量超过40的有2、3、4、5、7、8，共六个月．
【详解】
A、极差为：83-28=55，故本选项错误；
B、∵58出现的次数最多，是2次，
∴众数为：58，故本选项错误；
C、中位数为：（58+58）÷2=58，故本选项正确；
D、每月阅读数量超过40本的有2月、3月、4月、5月、7月、8月，共六个月，故本选项错误；
故选C．
6、A
【解析】
根据平行四边形的性质：①边：平行四边形的对边相等．②角：平行四边形的对角相等．③对角线：平行四边形的对角线互相平分；菱形的性质：①菱形具有平行四边形的一切性质；②菱形的四条边都相等； ③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角进行解答即可．
【详解】
菱形具有但平行四边形不一定具有的是对角线互相垂直，
故选A．
本题主要考查了菱形和平行四边形的性质，关键是熟练掌握二者的性质定理．
7、C
【解析】
首先判断△BAE、△CAD是等腰三角形，从而得出BA=BE，CA=CD，由△ABC的周长为26，及BC=10，可得DE=6，利用中位线定理可求出PQ．
8、A
【解析】
先证明AB=AF，DC=DE，再根据EF=AF+DE﹣AD，求出AD，即可得出答案.
【详解】
∵四边形是平行四边形
∴,,∥
∵平分，平分
∴,
∴,
∴
∴
∴
故选A
本题考查了平行四边形的性质，考点涉及平行线性质以及等角对等边等知识点，熟练掌握平行四边形的性质是解答本题的关键.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、．
【解析】
根据直线y=kx+b向上平移m（m＞0）个单位所得直线解析式为y=kx+b+m求解．
【详解】
解：把一次函数的图象向上平移3个单位后，得到的图象对应的函数关系式为．
故答案为：．
本题考查了一次函数图象与几何变换：直线y=kx+b向上平移m（m＞0）个单位所得直线解析式为y=kx+b+m，直线y=kx+b向下平移m（m＞0）个单位所得直线解析式为y=kx+b-m．
10、∠ABC=90°或AC=BD．
【解析】
试题分析：此题是一道开放型的题目，答案不唯一，添加一个条件符合正方形的判定即可．
解：条件为∠ABC=90°，
理由是：∵平行四边形ABCD的对角线互相垂直，
∴四边形ABCD是菱形，
∵∠ABC=90°，
∴四边形ABCD是正方形，
故答案为∠ABC=90°．
点睛：本题主要考查正方形的判定.熟练运用正方形判定定理是解题的关键.
11、C（0，-5）
【解析】
在Rt△ODC中，利用勾股定理求出OC即可解决问题
【详解】
解：∵A（12，13），
∴OD=12，AD=13，
∵四边形ABCD是菱形，
∴CD=AD=13，
在Rt△ODC中，，
∴C（0，-5）．
本题考查菱形的性质、勾股定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
12、
【解析】
由旋转的性质可得AB=AB'=，∠BAB'=15°，可得∠B'AD=∠BAC-∠B'AB=30°，由直角三角形的性质可得B'D=1，由三角形面积公式可求解．
【详解】
解：∵AB=BC，∠ABC=90°，
∴∠BAC=45°，
∵△ABC绕点A逆时针旋转15°后得到△AB′C′，
∴AB=AB'=，∠BAB'=15°，
∴∠B'AD=∠BAC-∠B'AB=30°，且∠B'=90°，
∵tan∠B'AD=,
∴AB'=B'D，
∴B'D=1，
∴阴影△ADC'的面积=，
故答案为：.
本题考查了旋转的性质，等腰直角三角形的性质，及锐角三角函数的知识，熟练运用旋转的性质是本题的关键．
13、45°
【解析】
先证明AB＝AE，求得∠AEB，由AD＝AE，∠DAE＝50°，求得∠AED，进而由角的和差关系求得结果．
【详解】
解：∵四边形ABCD是正方形，
∴AB＝AD，∠BAD＝90°，
∵AD＝AE，∠DAE＝50°，
∴AB＝AE，∠ADE＝∠AED＝65°，∠BAE＝140°，
∴∠ABE＝∠AEB＝20°，
∴∠BED＝65°−20°＝45°，
故答案为：45°．
本题主要考查了正方形的性质，等腰三角形的性质，三角形内角和定理，关键是求得∠AEB和∠AED的度数．
三、解答题（本大题共5个小题，共48分）
14、24
【解析】
试题分析：阴影部分的面积等于以AC、BC为直径的半圆的面积加上△ABC的面积减去以AB为直径的半圆的面积.
试题解析：根据Rt△ABC的勾股定理可得：AB=10，则S==24
考点：勾股定理
15、（1）见解析；（2）15°；（3）2+2．
【解析】
（1）在直角三角形ABC中，由AC=2AB，得到∠ACB=30°，再由折叠的性质得到一对角相等，利用等角对等边即可得证；
（2）由（1）得到△ABB′为等边三角形，利用矩形的性质及等边三角形的内角为60°，即可求出所求角度数；
（3）连接AF，过A作AM⊥BF，可得△AB′F是等腰直角三角形，△AB′B为等边三角形，分别利用三角函数定义求出MF与AM，根据AM=BM，即BM+MF=BF即可求出．
【详解】
（1）证明：∵在Rt△ABC中，AC=2AB，
∴∠ACB=∠AC′B′=30°，∠BAC=60°，
由旋转可得：AB′=AB，∠B′AC′=∠BAC=60°，
∴∠EAC′=∠AC′B′=30°，

∴AE=C′E；
（2）解：由（1）得到△ABB′为等边三角形，
∴∠AB′B=60°，即∠BB'F=∠AB'B+∠AB'F=150°，
∵BB'=B'F，
∴∠FBB′=∠B'FB=15°；
（3）解：连接AF，过A作AM⊥BF，可得△AB′F是等腰直角三角形，△AB′B为等边三角形，
∴∠AFB′=45°，∠BB′F=150°，
∵BB′=B′F，
∴∠B′FB=∠B′BF=15°，
∴∠AFM=30°，∠ABF=45°，
在Rt△AMF中，AM=BM=AB•cs∠ABM=2=2，
在Rt△AMF中，MF=AM=2，
则BF=2+2．
此题参考四边形综合题，旋转的性质，矩形的性质，锐角三角函数定义，等边三角形、直角三角形的性质，熟练掌握旋转的性质是解题的关键．
16、（1）（-，0）；（0，1）；（2）y=x+1或y=-x+1．
【解析】
试题分析：（1）根据坐标轴上点的坐标特征确定A点和B点坐标；
（2）由OA=，OP=2OA得到OP=1，分类讨论：当点P在x轴正半轴上时，则P点坐标为（1，0）；当点P在x轴负半轴上时，则P点坐标为（-1，0），然后根据待定系数法求两种情况下的直线解析式．
试题解析：（1）把x=0代入y=2x+1，得y═1，
则B点坐标为（0，1）；
把y=0代入y=2x+1，得0=2x+1，
解得x=-，
则A点坐标为（-，0）；
（2）∵OA=，
∴OP=2OA=1，
当点P在x轴正半轴上时，则P点坐标为（1，0），
设直线BP的解析式为：y=kx+b，
把P（1，0），B（0，1）代入得
解得：
∴直线BP的解析式为：y=-x+1；
当点P在x轴负半轴上时，则P点坐标为（-1，0），
设直线BP的解析式为y=kx+b，
把P（-1，0），B（0，1）代入得
解得:k=1，b=1
所以直线BP的解析式为：y=x+1；
综上所述，直线BP的解析式为y=x+1或y=-x+1．
考点：1.一次函数图象上点的坐标特征；2.待定系数法求一次函数解析式．
17、（1）30º，见解析．（2）
【解析】
（1）猜想：∠MBN=30°．如图1中，连接AN．想办法证明△ABN是等边三角形即可解决问题；
（2）MN=BM．折纸方案：如图2中，折叠△BMN，使得点N落在BM上O处，折痕为MP，连接OP．只要证明△MOP≌△BOP，即可解决问题.
【详解】
（1）猜想：∠MBN=30°．
证明：如图1中，连接AN，∵直线EF是AB的垂直平分线，
∴NA=NB，由折叠可知，BN=AB，
∴AB=BN=AN，
∴△ABN是等边三角形，
∴∠ABN=60°，
∴NBM=∠ABM=∠ABN=30°．
（2）结论：MN=BM．
折纸方案：如图2中，折叠△BMN，使得点N落在BM上O处，
折痕为MP，连接OP．
理由：由折叠可知△MOP≌△MNP，
∴MN=OM，∠OMP=∠NMP=∠OMN=30°=∠B，
∠MOP=∠MNP=90°，
∴∠BOP=∠MOP=90°，
∵OP=OP，
∴△MOP≌△BOP，
∴MO=BO=BM，
∴MN=BM．
本题考查翻折变换、矩形的性质、剪纸问题等知识，解题的关键是熟练掌握基本知识，学会添加常用辅助线，构造全等三角形解决问题．
18、（1）①P2，P3 ，②1≤x≤或≤x≤-1；（2）2-≤a≤1.
【解析】
（1）由已知结合图象，找到点P所在的区域；
（2）分别求出点A与B的坐标，由线段AB的位置，通过做圆确定正方形的位置．
【详解】
解：（1）①∵原点正方形边长为4，
当P1（0，0）时，正方形上与P1的最小距离是2，故不存在Q使P1Q≤1；
当P2（-1，1）时，存在Q（-2，1），使P2Q≤1；
当P3（3，2）时，存在Q（2，2），使P3Q≤1；
故答案为P₂、P₃；
②如图所示：阴影部分就是原点正方形友好点P的范围，
由计算可得，点P横坐标的取值范围是：
1≤x≤2+或-2-≤x≤-1；
（2）一次函数y=-x+2的图象分别与x轴，y轴交于点A，B，
∴A（0，2），B（2，0），
∵线段AB上存在原点正方形的友好点，
如图所示：
原点正方形边长a的取值范围2-≤a≤1．
本题考查一次函数的性质，新定义；能够将新定义的内容转化为线段，圆，正方形之间的关系，并能准确画出图形是解题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、k<6且k≠1
【解析】
分析：根据解分式方程的步骤，可得分式方程的解，根据分式方程的解是正数，可得不等式，解不等式，可得答案，并注意分母不分零．
详解：，
方程两边都乘以（x-1），得
x=2（x-1）+k，
解得x=6-k≠1，
关于x的方程程有一个正数解，
∴x=6-k＞0，
k＜6，且k≠1，
∴k的取值范围是k＜6且k≠1．
故答案为k＜6且k≠1．
点睛：本题主要考查了解分式方程、分式方程的解、一元一次不等式等知识，能根据已知和方程的解得出k的范围是解此题的关键．
20、1．
【解析】
首先根据求出外角度数，再利用外角和定理求出边数．
【详解】
正多边形的一个内角等于，
它的外角是：，
它的边数是：．
故答案为：1．
此题主要考查了多边形的外角与内角，做此类题目，首先求出正多边形的外角度数，再利用外角和定理求出求边数．
21、-
【解析】
根据Sn数的变化找出Sn的值每6个一循环，结合2018=336×6+2，即可得出S2018=S2，此题得解．
【详解】
解：S1=，S2=-S1-1=--1=-，S3==-，S4=-S3-1= ，=-（a+1），S6=-S5-1=（a+1）-1=a，S7= ，…，
∴Sn的值每6个一循环．
∵2018=336×6+2，
∴S2018=S2=-．
故答案为：-．
此题考查规律型中数字的变化类，根据数值的变化找出Sn的值，每6个一循环是解题的关键．
22、x＞1
【解析】
观察函数图象得到即可．
【详解】
解：由图象可得：当x＞1时，kx+b＞2，
所以不等式kx+b＞2的解集为x＞1，
故答案为：x＞1.
本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
23、48°
【解析】
根据旋转得出AC=DC，求出∠CDA，根据三角形内角和定理求出∠ACD，即可求出答案．
【详解】
∵将△ABC绕点C按逆时针方向旋转，得到△DCE，点A的对应点D落在AB边上，
∴AC=DC，
∵∠CAB=66°，
∴∠CDA=66°，
∴∠ACD=180°-∠A-∠CDA=48°，
∴∠BCE=∠ACD=48°，
故答案为：48°．
本题考查了三角形内角和定理，旋转的性质的应用，能求出∠ACD的度数是解此题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1），；（2）；（3）证明见解析.
【解析】
(1)根据题目中的例子直接写出结果；
(2)根据(1)中的特例，可以写出相应的猜想；
(3)根据(2)中的猜想，对等号左边的式子进行化简，即可得到等号右边的式子，从而可以解答本题.
【详解】
解：（1）由例子可得，
④为：==，⑤=，
（2）如果n为正整数，用含n的式子表示这个运算规律：= ，
（3）证明：∵n是正整数，
∴==．
即= ．
故答案为(1)==，=；(2)= ；(3)证明见解析.
本题考查了二次根式的混合运算、数字的变化类，解答本题的关键是明确题意，找出所求问题需要的条件.
25、（1）y＝2x（0≤x≤20），y＝2.5x﹣10（x＞20）；（2）5月份用水1吨，6月份用水量为30吨．
【解析】
（1）分别根据：未超过20吨时，水费y＝2×相应吨数；超过20吨时，水费y＝2×20+超过20吨的吨数×2.5；列出函数解析式；
（2）设该户居民5月份用水x吨，则6月份用水量为（45﹣m）吨，然后依据两个月共交水费95元列方程求解即可．
【详解】
解：（1）当0≤x≤20时，y＝2x；
当x＞20时，y＝2×20+2.5（x﹣20）＝2.5x﹣10；
（2）设该户居民5月份用水x吨，则6月份用水量为（45﹣m）吨，．
根据题意，得：2m+2.5（45﹣m）﹣10＝95，
解得：m＝1．
答：该户居民5月份用水1吨，6月份用水量为30吨．
故答案为（1）y＝2x（0≤x≤20），y＝2.5x﹣10（x＞20）；（2）5月份用水1吨，6月份用水量为30吨．
本题考查了一次函数的应用、一元一次方程的应用；得到用水量超过20吨的水费的关系式是解决本题的关键．
26、（1）；（2）－1；（3）2
【解析】
（1）先求出点P为（1，2），再把P点代入解析式即可解答.
（2）把P（1，2）代入y＝ax+3，即可解答.
（3）根据y＝x+1与x轴的交点为（﹣1，0），y＝﹣x+3与x轴的交点为（3，0），即可得到这两个交点之间的距离，再根据三角形的面积公式，即可解答.
【详解】
（1）把x＝1代入y＝x+1，得出y＝2，
函数y＝x+1和y＝ax+3的图象交于点P（1，2），
即x＝1，y＝2同时满足两个一次函数的解析式．
所以关于x，y的方程组 的解是 ．
故答案为；
（2）把P（1，2）代入y＝ax+3，
得2＝a+3，解得a＝﹣1．
故答案为﹣1；
（3）∵函数y＝x+1与x轴的交点为（﹣1，0），
y＝﹣x+3与x轴的交点为（3，0），
∴这两个交点之间的距离为3﹣（﹣1）＝2，
∵P（1，2），
∴函数y＝x+1和y＝ax+3的图象与x轴围成的几何图形的面积为：×2×2＝2．
此题考查一次函数与二元一次方程，解题关键在于把已知点代入解析式求解.
题号
一
二
三
四
五
总分
得分
批阅人