2024-2025学年河南省洛阳市强基联盟高二（上）联考数学试卷（10月份）（含答案）

这是一份2024-2025学年河南省洛阳市强基联盟高二（上）联考数学试卷（10月份）（含答案），共9页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。
1.在空间四边形PABC中，PB−AB+AC=( )
A. APB. PCC. ABD. AC
2.在空间直角坐标系Oxyz中，点A(1,1,2)关于x轴对称点的坐标为( )
A. (1,1,−2)B. (−1,1,2)C. (1,−1,−2)D. (1,−1,2)
3.《九章算术》是我国东汉初年编订的一部数学经典著作，其在卷第五《商功》中描述的几何体“阳马”实为“底面为矩形，一侧棱垂直于底面的四棱锥”.如图，在“阳马”A−OBCD中，E为△ACD的重心，若AB=a，AC=b，AD=c，则BE=( )
A. −a+12b+12c
B. −a+13b+13c
C. a+23b+23c
D. −a+13b−13c
4.设a=(1,1,0)，b=(t,0,1)分别为两平面的法向量，若两平面所成的角为60°，则t等于( )
A. 1B. −1C. −1或1D. 2
5.已知A(1,2,−1)为平面α内一点，若平面α的法向量为n=(1,−1,1)，则点P(−1,1,3)到平面α的距离为( )
A. 2B. 3C. 2D. 1
6.已知空间中三点A(0,0,0)，B(1,−1,2)，C(−1,−2,1)，则以AB，AC为邻边的平行四边形的面积为( )
A. 32B. 3 32C. 3D. 3 3
7.已知向量a=(2,−3,0)，b=(0,3,4)，则向量a在向量b上的投影向量的坐标为( )
A. (−1813,2713,0)B. (1813,−2713,0)C. (0,2725,3625)D. (0,−2725,−3625)
8.在正三棱柱ABC−A1B1C1中，AB=2，AA1= 3，BC=2BO，M为棱B1C1上的动点，N为线段AM上的动点，且MNMO=MOMA，则线段MN长度的最小值为( )
A. 2B. 3C. 3 32D. 62
二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。
9.若{a,b,c}是空间的一个基底，则下列各组中能构成空间的一个基底的是( )
A. a+b，a−b，c
B. a+b，b+c，c+a
C. 3a−4b，2b−3c，3a−6c
D. a+b，a+b+c，2c
10.如图，四边形ABCD，ABEF都是边长为2的正方形，平面ABCD⊥平面ABEF，P，Q分别是线段AE，BD的中点，则( )
A. PQ//DF
B. 异面直线AQ，PF所成角为π6
C. 点P到直线DF的距离为 62
D. △DFQ的面积是 2
11.在平行六面体ABCD−A1B1C1D1中，AB=AD=AA1=2，∠DAB=∠A1AB=∠A1AD=60°，若AQ=mAB+nAD+pAA1，其中m，n，p∈[0,1]，则下列结论正确的为( )
A. 若点Q在平面A1B1C1D1内，则p=1
B. 若CQ⊥DB，则m=n
C. 当p=12时，三棱锥Q−ABD的体积为9 28
D. 当m+n=1时，CQ长度的最小值为 2
三、填空题：本题共3小题，每小题5分，共15分。
12.设向量a=(1,m,3)，b=(4,−1,0)，若a⊥b，则m= ______．
13.在空间直角坐标系O−xyz中，点A，B，C，M的坐标分别是(2,0,2)，(2,1,0)，(0,4,−1)，(0,m,−5)，若A，B，C，M四点共面，则m=______．
14.如图，在三棱锥O−ABC中，点G为底面△ABC的重心，点M是线段OG上靠近点G的三等分点，过点M的平面分别交棱OA，OB，OC于点D，E，F，若OD=kOA，OE=mOB，OF=nOC，则1k+1m+1n=______．
四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题13分)
已知空间向量a=(1,2,12),b=(12,−12,1),c=(−2,3,−12),d=(1,−32,14)．
(1)求(a+c)⋅b；
(2)判断a与b以及c与d的位置关系．
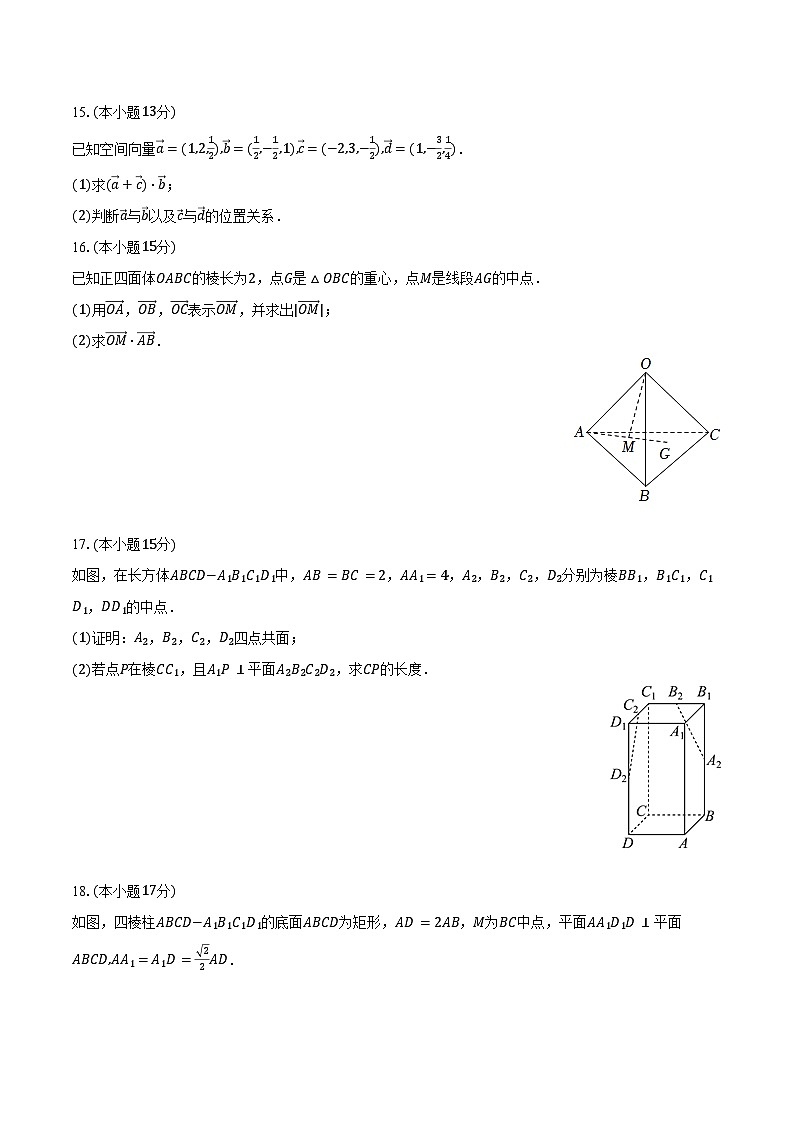
16.(本小题15分)
已知正四面体OABC的棱长为2，点G是△OBC的重心，点M是线段AG的中点．
(1)用OA，OB，OC表示OM，并求出|OM|；
(2)求OM⋅AB．
17.(本小题15分)
如图，在长方体ABCD−A1B1C1D1中，AB=BC=2，AA1=4，A2，B2，C2，D2分别为棱BB1，B1C1，C1D1，DD1的中点．
(1)证明：A2，B2，C2，D2四点共面；
(2)若点P在棱CC1，且A1P⊥平面A2B2C2D2，求CP的长度．
18.(本小题17分)
如图，四棱柱ABCD−A1B1C1D1的底面ABCD为矩形，AD=2AB，M为BC中点，平面AA1D1D⊥平面ABCD,AA1=A1D= 22AD．
(1)证明：A1D⊥平面ABB1A1；
(2)求二面角B−A1A−M的平面角的余弦值．
19.(本小题17分)
在三棱台ABC−A1B1C1中，CC1⊥平面ABC，AB=BC=AC=2A1B1=2，D，E分别为CA，CB的中点．
(1)证明：A1B/​/平面C1DE；
(2)已知BC1⊥A1C，F为线段AB上的动点(包括端点)．
①求三棱台A1B1C1−ABC的体积；
②求C1F与平面ABB1A1所成角的正弦值的最大值．
参考答案
1.B
2.C
3.B
4.C
5.B
6.D
7.D
8.D
9.AB
10.AC
11.ABD
12.4
13.6
14.92
15.解：(1)由题知，a+c=(−1,5,0)，
所以(a+c)⋅b=(−1,5,0)⋅(12,−12,1)=−3；
(2)因为a=(1,2,12),b=(12,−12,1)，
所以a⋅b=1×12+2×(−12)+12×1=0，
所以a⊥b；
因为c=(−2,3,−12),d=(1,−32,14)，
所以c=−2(1,−32,14)=−2d，所以c/​/d．
16.解：(1)∵点M是线段AG的中点，
∴OM=12OA+12OG=12OA+12×23(12OB+12OC)=12OA+16OB+16OC，
∵OA⋅OB=OB⋅OC=OA⋅OC=2×2×cs60°=2，
∴|OM|2=OM2=14OA2+136OB2+136OC2+16OA⋅OB+16OA⋅OC+118OB⋅OC
=14×4+136×4+136×4+16×2+16×2+118×2=2，
∴|OM|= 2．
(2)OM⋅AB=(12OA+16OB+16OC)⋅(OB−OA)=13OA⋅OB−12OA2+16OB2+16OB⋅OC−16OA⋅OC
=13×2−12×4+16×4+16×2−16×2=−23．
17.(1)证明：连接B2C2，B1D1，A2D2，

因为A2，B2，C2，D2分别为棱BB1，B1C1，C1D1，DD1的中点，
所以B1A2//D1D2，且B1A2=D1D2，
所以四边形A2B1D1D2为平行四边形，
所以B1D1//A2D2，又B1D1//B2C2，
所以B2C2//A2D2，所以A2，B2，C2，D2四点共面；
(2)解：以C为坐标原点，以CD，CB，CC1所在直线为x，y，z轴建立空间直角坐标系，

由AB=BC=2，AA1=4，A2，B2，C2，D2分别为棱BB1，B1C1，C1D1，DD1的中点，
可得A2(0,2,2)，B2(0,1,4)，C2(1,0,4)，A1(2,2,4)，
则B2A2=(0,1,−2)，C2B2=(−1,1,0)，
设CP=t(0≤t≤4)，即P(0,0,t)，则A1P=(−2,−2,t−4)，
由A1P⊥平面A2B2C2D2，故A1P⋅B2A2=0A1P⋅C2B2=0，
即−2×0−2×1+(t−4)×(−2)=0−2×(−1)+(−2)×1+(t−4)×0=0，解得t=3，
所以CP=3．
18.解(1)证明：∵底面ABCD是矩形，
∴AB⊥AD，
又平面AA1D1D⊥平面ABCD，平面AA1D1D∩平面ABCD=AD，AB⊂平面ABCD，
∴AB⊥平面AA1D1D，
又A1D⊂平面AA1D1D，
∴AB⊥A1D，
∵AA1=A1D= 22AD，
∴AA12+A1D2=AD2，
∴AA1⊥A1D，
又AA1∩AB=A，AA1，AB⊂平面ABB1A1，
∴A1D⊥平面ABB1A1；
(2)取AD的中点O，连接A1O，
∵A1A=A1D，
∴A1O⊥AD，
又平面AA1D1D⊥平面ABCD，平面AA1D1D∩平面ABCD=AD，A1O⊂平面AA1D1D，
∴A1O⊥平面ABCD，连接OM，
又底面ABCD为矩形，
∴OM⊥AD，
∴OM，AD，OA1两两互相垂直，
建立以O为坐标原点的空间直角坐标系，如图所示：

设AB=1，
则A(0,−1,0)，D(0,1,0)，A1(0,0,1)，M(1,0,0)，
∴AA1=(0,1,1),A1D=(0,1,−1),AM=(1,1,0)，
由(1)得A1D⊥平面ABB1A1，则A1D是平面ABB1A1的一个法向量，
设平面A1AM的一个法向量为n=(x,y,z)，则n⋅AA1=y+z=0n⋅AM=x+y=0，取x=1，则y=−1，z=1，
则n=(1,−1,1)，
设二面角B−A1A−M的平面角为θ，则|csθ|=|A1D⋅n||A1D|⋅|n|=2 2× 3= 63，
由图可得二面角B−A1A−M的平面角为锐角，
∴二面角B−A1A−M的平面角的余弦值为 63．
19.解：(1)证明：设A1C交C1D于点G，连接EG，
在三棱台ABC−A1B1C1中，A1C1/​/AC，A1C1=12AC，又D为AC的中点，
所以A1C1//DC，又A1C1=DC，
所以四边形A1C1CD是平行四边形，G为A1C的中点，
又E为BC的中点，
所以EG/​/A1B，又EG⊂平面C1DE，A1B⊄平面C1DE，
所以A1B/​/平面C1DE．
(2)①连接BD，因为CC1⊥平面ABC，且CC1⊂平面AA1C1C，
所以平面ABC⊥平面AA1C1C，
因为AB=BC，D为CA的中点，
所以BD⊥AC，又平面ABC∩平面AA1C1C=AC，BD⊂平面ABC，
所以BD⊥平面AA1C1C，因为A1C⊂平面AA1C1C，
所以BD⊥A1C，
又BC1⊥A1C，BC1∩BD=B，BC1，BD⊂平面BDC1，
所以A1C⊥平面BDC1，A1C⊥DC1，
故四边形A1C1CD为菱形，即CC1=1，
所以三棱台A1B1C1−ABC的体积为13×1×( 34+ 3+ 3× 34)=7 312．
②如图所示建立平面直角坐标系，则C1(0,0,1)，A1(1,0,1)，A(2,0,0)，B(1, 3,0)，不妨设FA=λBA，λ∈[0,1]，则F(2−λ, 3λ,0)，C1F=(2−λ, 3λ,−1)，

设平面ABB1A1的一个法向量为n=(x,y,z)，
则n⊥AA1n⊥AB，即n⋅AA1=0n⋅AB=0，得−x+z=0−x+ 3y=0，
令y=1，可得n=( 3,1, 3)，
设C1F与平面ABB1A1所成角为θ，
则sinθ=|cs|= 3 7× (2λ−1)2+4≤ 2114，
当且仅当λ=12时，等号成立，
所以C1F与平面ABB1A1所成角的正弦值的最大值为 2114．