吉林省四平市第14中学2024年九年级数学第一学期开学综合测试模拟试题【含答案】

这是一份吉林省四平市第14中学2024年九年级数学第一学期开学综合测试模拟试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
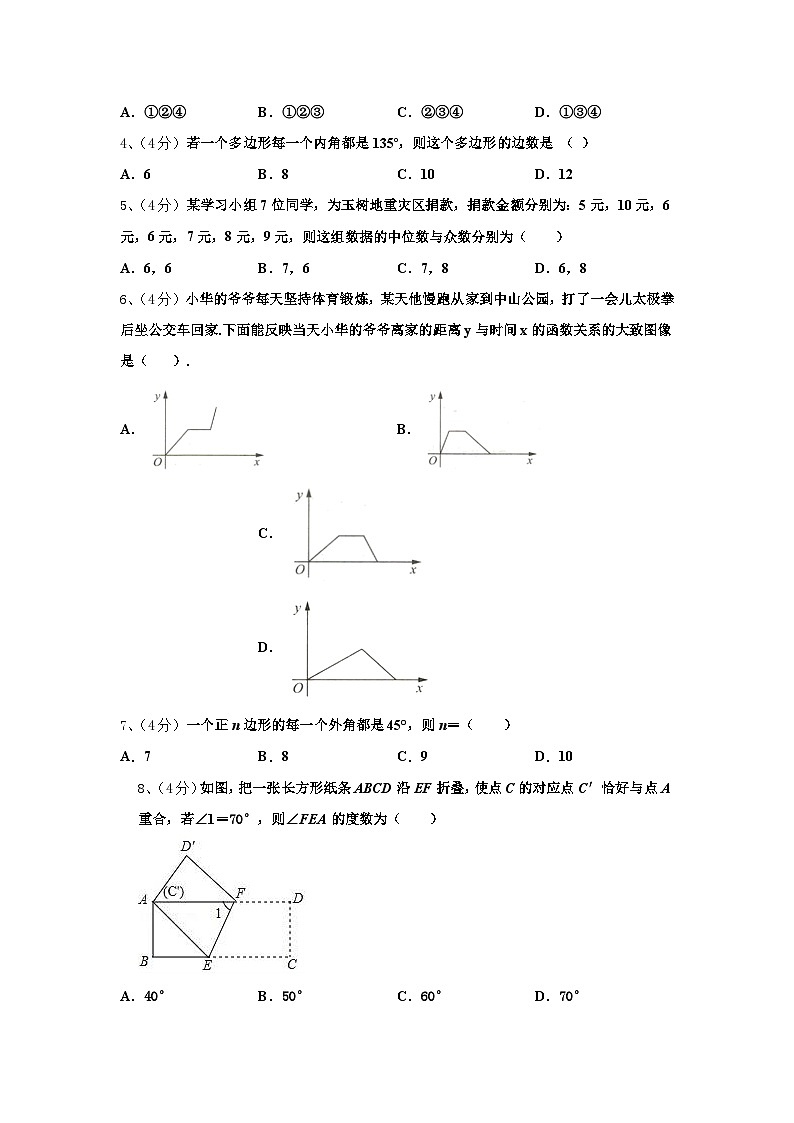
1、（4分）一名考生步行前往考场，10分钟走了总路程的，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1），则他到达考场所花的时间比一直步行提前了（ ）
A．20分钟 B．22分钟 C．24分钟 D．26分钟
2、（4分）如图，在中，，，点D是AB的中点，则
A．4B．5C．6D．8
3、（4分）在平行四边形ABCD中,AB=3,BC=4,当平行四边形ABCD的面积最大时,下结论正确的有( )
①AC=5 ②∠A+∠C=180° ③AC⊥BD ④AC=BD
A．①②④B．①②③C．②③④D．①③④
4、（4分）若一个多边形每一个内角都是135º，则这个多边形的边数是 （ ）
A．6B．8C．10D．12
5、（4分）某学习小组7位同学，为玉树地重灾区捐款，捐款金额分别为：5元，10元，6元，6元，7元，8元，9元，则这组数据的中位数与众数分别为（ ）
A．6，6B．7，6C．7，8D．6，8
6、（4分）小华的爷爷每天坚持体育锻炼，某天他慢跑从家到中山公园，打了一会儿太极拳后坐公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图像是（ ）.
A．B．C．D．
7、（4分）一个正n边形的每一个外角都是45°，则n＝（ ）
A．7B．8C．9D．10
8、（4分）如图，把一张长方形纸条ABCD沿EF折叠，使点C的对应点C′恰好与点A重合，若∠1＝70°，则∠FEA的度数为（ ）
A．40°B．50°C．60°D．70°
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）正十边形的外角和为__________．
10、（4分）设x1，x2是一元二次方程x2﹣x﹣1＝0的两根，则x1+x2+x1x2＝_____．
11、（4分）小华用S2={（x1-8）2+（x2-8）2+……+（x10-8）2计算一组数据的方差，那么x1+x2+x3+…+x10=____________．
12、（4分）如图，平行四边形ABCD在平面直角坐标系中，已知∠DAB＝60°，A（﹣2，0），点P在AD上，连接PO，当OP⊥AD时，点P到y轴的距离为_____．
13、（4分）已知正n边形的一个外角是45°，则n＝____________
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，▱ABCD中，E是AB的中点，连结CE并延长交DA的延长线于点F．求证：AFAD．
15、（8分）化简分式（）÷ ，并在 2，3，4，5 这四个数中取一个合适的数作为 a 的值代入求值．
16、（8分） “西瓜足解渴，割裂青瑶肤”，西瓜为夏季之水果，果肉味甜，能降温去暑；种子含油，可作消遣食品；果皮药用，有清热、利尿、降血压之效.某西瓜批发商打算购进“黑美人”西瓜与“无籽”西瓜两个品种的西瓜共70000千克．
（1）若购进“黑美人”西瓜的重量不超过“无籽”西瓜重量的倍，求“黑美人”西瓜最多购进多少千克？
（2）该批发商按（1）中“黑美人”西瓜最多重量购进，预计“黑美人”西瓜售价为4元/千克；“无籽”西瓜售价为5元/千克，两种西瓜全部售完.由于存储条件的影响，“黑美人”西瓜与“无籽”西瓜分别有与的损坏而不能售出.天气逐渐炎热，西瓜热卖，“黑美人”西瓜的销售价格上涨，“无籽”西瓜的销售价格上涨，结果售完之后所得的总销售额比原计划下降了3000元，求的值．
17、（10分）某校七、八年级各有学生400人，为了解这两个年级普及安全教育的情况，进行了抽样调查，过程如下
选择样本,收集数据从七、八年级各随机抽取20名学生,进行安全教育考试,测试成绩(百分制)如下：
七年级 85 79 89 83 89 98 68 89 79 59
99 87 85 89 97 86 89 90 89 77
八年级 71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
分组整理，描述数据
(1)按如下频数分布直方图整理、描述这两组样本数据，请补全八年级20名学生安全教育频数分布直方图；
(2)两组样本数据的平均数、中位数、众数、优秀率如下表所示，请补充完整；
得出结论，说明理由.
(3)整体成绩较好的年级为___,理由为___(至少从两个不同的角度说明合理性).
18、（10分）矩形中，对角线、交于点，点、、分别为、、的中点.
（1）求证：四边形为菱形；
（2）若，，求四边形的面积.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若函数是正比例函数，则常数m的值是 。
20、（4分）将直线y=2x-3平移，使之经过点(1，4)，则平移后的直线是____．
21、（4分）如图，正方形的边长为12，点、分别在、上，若，且，则______．
22、（4分）某公司招聘考试分笔试和面试两项，其中笔试按，面试按计算加权平均数作为总成绩.马丁笔试成绩85分，面试成绩90分，那么马丁的总成绩是______分.
23、（4分）两条平行线间的距离公式
一般地；两条平行线间的距离公式
如：求：两条平行线的距离．
解：将两方程中的系数化成对应相等的形式，得
因此，
两条平行线的距离是____________．
二、解答题（本大题共3个小题，共30分）
24、（8分）实践与探究
宽与长的比是（约0.618）的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计。
下面我们通过折纸得到黄金矩形。
第一步，在一张矩形纸片的一端，利用图1的方法折出一个正方形，然后把纸片展平。
第二步，如图2，把这个正方形折成两个相等的矩形，再把纸片展平，折痕是。
第三步，折出内侧矩形的对角线，并把折到图3中所示的处，折痕为。
第四步，展平纸片，按照所得的点折出，使；过点折出折痕，使。
（1）上述第三步将折到处后，得到一个四边形，请判断四边形的形状，并说明理由。
（2）上述第四步折出折痕后得到一个四边形，这个四边形是黄金矩形，请你说明理由。（提示：设的长度为2）
（3）在图4中，再找出一个黄金矩形_______________________________（黄金矩形除外，直接写出答案，不需证明，可能参考数值：）
（4）请你举一个采用了黄金矩形设计的世界名建筑_________________________.
25、（10分）如图，在正方形中，点为延长线上一点且，连接，在上截取，使，过点作平分，，分别交于点、.连接.
（1）若，求的长；
（2）求证：.
26、（12分）某校300名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2），经确认扇形图是正确的，而条形图尚有一处错误．
回答下列问题：
（1）条形图中存在错误的类型是 ，人数应该为 人；
（2）写出这20名学生每人植树量的众数 棵，中位数 棵；
（3）估计这300名学生共植树 棵．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
试题解析：他改乘出租车赶往考场的速度是÷2=，所以到考场的时间是10+÷=16分钟，
∵10分钟走了总路程的，
∴步行的速度=÷10=，
∴步行到达考场的时间是1÷=40，则他到达考场所花的时间比一直步行提前了40-16=24分钟．
故选C．
考点：函数的图象．
2、B
【解析】
根据直角三角形中，斜边上的中线等于斜边的一半解答即可．
【详解】
，点D为AB的中点，
．
故选：B．
本题考查直角三角形的性质，掌握在直角三角形中斜边上的中线等于斜边的一半是解题的关键．
3、A
【解析】
当▱ABCD的面积最大时，四边形ABCD为矩形，得出∠A=∠B=∠C=∠D=90°，AC=BD，根据勾股定理求出AC，即可得出结论．
【详解】
根据题意得：当▱ABCD的面积最大时，四边形ABCD为矩形，
∴∠BAD=∠ABC=∠BCD=∠CDA=90°，AC=BD，
∴∠BAD+∠BCD=180° ，AC==5，
①正确，②正确，④正确；③不正确；
故选A．
本题考查了平行四边形的性质、矩形的性质以及勾股定理；得出▱ABCD的面积最大时，四边形ABCD为矩形是解决问题的关键．
4、B
【解析】
试题分析：设多边形的边数为n，则=135，解得：n=8
考点：多边形的内角.
5、B
【解析】
首先把所给数据按从小到大的顺序重新排序，然后利用中位数和众数的定义就可以求出结果．
【详解】
解：把已知数据按从小到大的顺序排序后为5元，1元，1元，7元，8元，9元，10元，
∴中位数为7
∵1这个数据出现次数最多，
∴众数为1．
故选B．
本题结合众数与中位数考查了确定一组数据的中位数的能力．注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求．如果是偶数个则找中间两位数的平均数．众数只要找次数最多的即可．
6、C
【解析】
根据在每段中，离家的距离随时间的变化情况即可进行判断．
【详解】
图象应分三个阶段，第一阶段：慢步到离家较远的绿岛公园，在这个阶段，离家的距离随时间的增大而增大；第二阶段：打了一会儿太极拳，这一阶段离家的距离不随时间的变化而改变。故D错误；第三阶段：搭公交车回家，这一阶段，离家的距离随时间的增大而减小，故A错误，并且这段的速度大于第一阶段的速度，则B错误.
故选：C.
本题考查函数图象，解题的关键是由题意将图象分为三个阶段进行求解.
7、B
【解析】
根据正多边形的边数=360°÷每一个外角的度数，进行计算即可得解．
【详解】
解：n=360°÷45°=1．
故选：B．
本题考查了多边形的外角，熟记正多边形的边数、每一个外角的度数、以及外角和360°三者之间的关系是解题的关键．
8、D
【解析】
根据翻折不变性即可解决问题；
【详解】
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠1＝∠FEC，
由翻折不变性可知：∠FEA＝∠FEC，
∵∠1＝70°，
∴∠FEA＝70°，
故选D．
本题考查了矩形的性质、平行线的性质、翻折变换等知识，解题的关键是灵活运用所学知识解决问题．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、360°
【解析】
根据多边形的外角和是360°即可求出答案．
【详解】
∵任意多边形的外角和都是360°，
∴正十边形的外交和是360°，
故答案为：360°．
此题考查多边形的外角和定理，熟记定理是解题的关键．
10、1
【解析】
根据根与系数的关系得到x1+x2＝1，x1×x2＝﹣1，然后利用整体思想进行计算．
【详解】
解：∵x1、x2是方程x2﹣x﹣1＝1的两根，
∴x1+x2＝1，x1×x2＝﹣1，
∴x1+x2+x1x2＝1﹣1＝1．
故答案为：1．
此题考查根与系数的关系，解题关键在于得到x1+x2＝1，x1×x2＝﹣1.
11、1
【解析】
根据S2=[（x1-8）2+（x2-8）2+……+（x10-8）2]可得平均数为8，进而可得答案．
【详解】
解：由S2=[（x1-8）2+（x2-8）2+……+（x10-8）2]知这10个数据的平均数为8，
则x1+x2+x3+…+x10=10×8=1，
故答案为：1．
此题主要考查了方差公式，关键是掌握方差公式：一般地设n个数据，x1，x2，…xn的平均数为，则方差S2=[（x1-）2+（x2-）2+…+（xn-）2]．
12、
【解析】
首先根据点A的坐标求得OA的长，然后求得PO的长，从而求得点P到y轴的距离即可．
【详解】
解：∵A（﹣2，0），
∴OA＝2，
∵∠DAB＝60°，OP⊥AD，
∴∠AOP=30°，
∴AP=1，
∴OP＝，
作PE⊥y轴，
∵∠POA＝30°，
∴∠OPE＝30°，
∴OE=
∴PE＝，
∴点P到y轴的距离为，
故答案为：．
考查了平行四边形的性质，能够将点的坐标转化为线段的长是解答本题的关键，难度不大．
13、8
【解析】
解：∵多边形的外角和为360°，正多边形的一个外角45°，
∴多边形得到边数360÷45=8，所以是八边形．
故答案为8
三、解答题（本大题共5个小题，共48分）
14、详见解析.
【解析】
由在▱ABCD中，点E为AB的中点，易证得△AFE≌△BCE (ASA) ,然后由全等三角形的对应边相等得出AF=BC，即可证得结论.
【详解】
证明：∵平行四边形ABCD
∴AD∥BC，AD=BC (平行四边形对边平行且相等).
又∵AD∥BC
∴∠BCF=∠F(两直线平行内错角相等).
∠BAF=∠ABC
∵E为AB中点
在△AFE和△BCE中
∠BCF=∠F
∠BAF=∠ABC
AE=EB
∴△AFE≌△BCE (ASA)
∴AF=BC(全等三角形对应边相等)
∴AF=AD（等量代换）
此题考查全等三角形的判定与性质，平行四边形的性质，解题关键在于证明△AFE≌△BCE.
15、，取代入，原式．
【解析】
先根据分式混合运算顺序和运算法则化简原式，再选取是分式有意义a的值代入计算可得．
【详解】
解：原式=·
=·
=·
=a+3，
∵a≠﹣3，2，3，
∴a=4或5，
当a=4时，原式=4+3=7；
当a=5时，原式=5+3=8.
本题主要考查分式的混合运算，解题的关键是掌握分式混合运算顺序和运算法则及分式有意义的条件．
16、（1）最多（2）
【解析】
（1）设购进“黑美人”西瓜千克，则购进“无籽”西瓜千克，根据购进“黑美人”西瓜的重量不超过“无籽”西瓜重量的倍，即可得出关于的一元一次不等式，解之取其最大值即可得出结论； （2）根据总价=单价×数量，即可得出关于的一元二次方程，解之取其正值即可得出结论．
【详解】
解：（1）设购进“黑美人”西瓜千克，则购进“无籽”西瓜千克， 依题意，得：，
解得：．
答：“黑美人”西瓜最多购进40000千克．
（2）由题意得： ，
整理，得：，
解得：（舍去）．
答：的值为1．
本题考查了一元一次不等式的应用以及一元二次方程的应用，解题的关键是：（1）根据各数量之间的关系，正确列出一元一次不等式；（2）找准等量关系，正确列出一元二次方程．
17、（1）见解析；（2）91.5，94，55%；（3）八年级，八年级的中位数和优秀率都高于七年级.
【解析】
（1）由收集的数据即可得；根据题意不全频数分布直方图即可；
（2）根据众数和中位数和优秀率的定义求解可得；
（3）八年级的中位数和优秀率都高于七年级即可的结论．
【详解】
(1)补全八年级20名学生安全教育频数分布直方图如图所示，
(2)八年级20名学生安全教育考试成绩按从小到大的顺序排列为：51 55 62 71 78 85 86 87 88 91 92 94 94 94 94 94 97 98 98 99
∴中位数==91.5分；
∵94分出现的次数最多，故众数为94分；
优秀率为：×100%=55%，
故答案为：91.5，94，55%；
(3)整体成绩较好的年级为八年级，理由为八年级的中位数和优秀率都高于七年级。
故答案为：八年级，八年级的中位数和优秀率都高于七年级.
此题考查条形统计图，中位数，众数，解题关键在于看懂图中数据.
18、（1）见解析；（2）.
【解析】
（1）根据三角形的中位线定理即可证明；
（2）根据菱形的面积公式即可求解.
【详解】
（1）∵四边形是矩形，
∴，
又∵点、、分别为、、的中点，
∴，，且，
同理，，
故，
∴四边形为菱形；
（2）连接、，则，且，
，且，
由（1）知，四边形为菱形，
故.
此题主要考查菱形的判定与面积求解，解题的关键是熟知菱形的判定定理.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、-3
【解析】
根据函数是正比例函数知x的幂是一次得，m=±3，m=3不符合题意，舍去得m=-3.
20、y=2x+2
【解析】
【分析】先由平移推出x的系数是2，可设直线解析式是y=2x+k,把点（1，4）代入可得.
【详解】由已知可设直线解析式是y=2x+k,
因为，直线经过点（1，4）,
所以，4=2+k
所以，k=2
所以，y=2x+2
故答案为y=2x+2
【点睛】本题考核知识点：一次函数性质.解题关键点：熟记一次函数性质.
21、
【解析】
首先延长FD到G，使DG＝BE，利用正方形的性质得∠B＝∠CDF＝∠CDG＝90°，CB＝CD；利用SAS定理得△BCE≌△DCG，利用全等三角形的性质易证△GCF≌△ECF，利用勾股定理可得DF，求出AF，设BE＝x，利用GF＝EF，解得x，再利用勾股定理可得CE．
【详解】
解：如图，延长FD到G，使DG＝BE；
连接CG、EF；
∵四边形ABCD为正方形，
在△BCE与△DCG中，，
∴△BCE≌△DCG（SAS），
∴CG＝CE，∠DCG＝∠BCE，
∴∠GCF＝45°，
在△GCF与△ECF中，，
∴△GCF≌△ECF（SAS），
∴GF＝EF，
∵DF＝，AB＝AD＝12，
∴AF＝12−4＝8，
设BE＝x，则AE＝12−x，EF＝GF＝4＋x，
在Rt△AEF中，由勾股定理得：（12−x）2＋82＝（4＋x）2，
解得：x＝6，
∴BE＝6，
∴CE＝，
故答案为．
本题主要考查了全等三角形的判定及性质，勾股定理等，构建全等三角形，利用方程思想是解答此题的关键．
22、1
【解析】
根据笔试和面试所占的权重以及笔试成绩和面试成绩，列出算式，进行计算即可．
【详解】
小明的总成绩为85×60%+90×40%=1（分）．
故答案为：1．
本题考查了加权平均数，关键是根据加权平均数的计算公式列出算式，用到的知识点是加权平均数．
23、1
【解析】
试题分析：认真读题，可知A=3，B=4，C1=-10，C2=-5，代入距离公式为===1.
二、解答题（本大题共3个小题，共30分）
24、（1）四边形是菱形，见解析；（2）见解析；（3）黄金矩形（或黄金矩形）；（4）希腊的巴特农神庙（或巴黎圣母院）.
【解析】
（1）根据菱形的判定即可求解；
（2）根据菱形的性质及折叠得到，即可证明；
（3）
【详解】
（1）解：
四边形是菱形，
理由如下：
由矩形纸片可得，
∴，
由折叠可得，
∴，
∴，
又由折叠可得，
∴，
∴四边形是菱形；
（2）证明：设的长度为2，
由正方形可得，，
∴，
∵，
∴，
∴，
∴四边形是矩形，
∵，由折叠可得，，
在中，根据勾股定理，，
由折叠可得，
∴，
∴，
∴矩形是黄金矩形；
（3）黄金矩形
理由：AG=AD+DG=AB+DG=
AH=2，
∴
∴四边形AGEH为黄金矩形
（4）希腊的巴特农神庙（或巴黎圣母院）
此题主要考查矩形的性质与判定，解题的关键是熟知特殊平行四边形的判定与性质.
25、（1）6-；（2）证明见详解
【解析】
（1）由正方形性质和等腰直角三角形性质及勾股定理即可求得结论；
（2）过点D作DM⊥CF于点M，证明△DCM≌△CBH，再证明△BHG、△DMG都是等腰直角三角形，根据等腰直角三角形斜边与直角边的数量关系即可．
【详解】
解：（1）∵ABCD是正方形
∴AB=AD=BC=CD，∠BAD=∠BAE=∠BCD=90°，
∵BF=AD=
∴AB=AD=AE=
∴BE==
∴EF=BE-BF=6-，
（2）如图，过点D作DM⊥CF于点M，则∠CDM+∠DCM=90°，
∵∠DCM+∠BCH=90°
∴∠CDM=∠BCH
∵∠BAE=90°，AB=AE
∴∠ABE=45°
∵BH⊥CF
∴∠BHC=∠CMD=90°，∠FBH=∠CBF=×（90°+45°）=67.5°
在△DCM和△CBH中，

∴△DCM≌△CBH（AAS）
∴DM=CH，CM=BH
∵BG平分∠ABF
∴∠FBG=∠ABE=22.5°
∴∠HBG=∠FBH-∠FBG=45°
∴△BHG是等腰直角三角形，
∴BH=HG，BG=BH=CM
∴CM=HG
∴CH=GM
∴DM=GM
∴△DMG是等腰直角三角形，
∴DG=GM，
∴DG+BG=GM+CM=（GM+CM）=CG
本题考查了正方形性质，等腰直角三角形判定和性质，勾股定理，全等三角形判定和性质等，解题关键是正确添加辅助线构造全等三角形．
26、（1）D，2；（2）5， 5；（3）1．
【解析】
（1）利用总人数乘对应的百分比求解即可；
（2）根据众数、中位数的定义即可直接求解；
（3）首先求得调查的20人的平均数，乘以总人数300即可．
【详解】
（1）D错误，理由：20×10%＝2≠3；
故答案为：D，2；
（2）由题意可知，植树5棵人数最多，故众数为5，
共有20人植树，其中位数是第10、11人植树数量的平均数，
即（5+5）＝5，故中位数为5；
故答案为：5，5；
（3）（4×4+5×8+6×6+7×2）÷20＝5.3，
∴300名学生共植树5.3×300＝1（棵）．
故答案为：1．
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
题号
一
二
三
四
五
总分
得分
批阅人