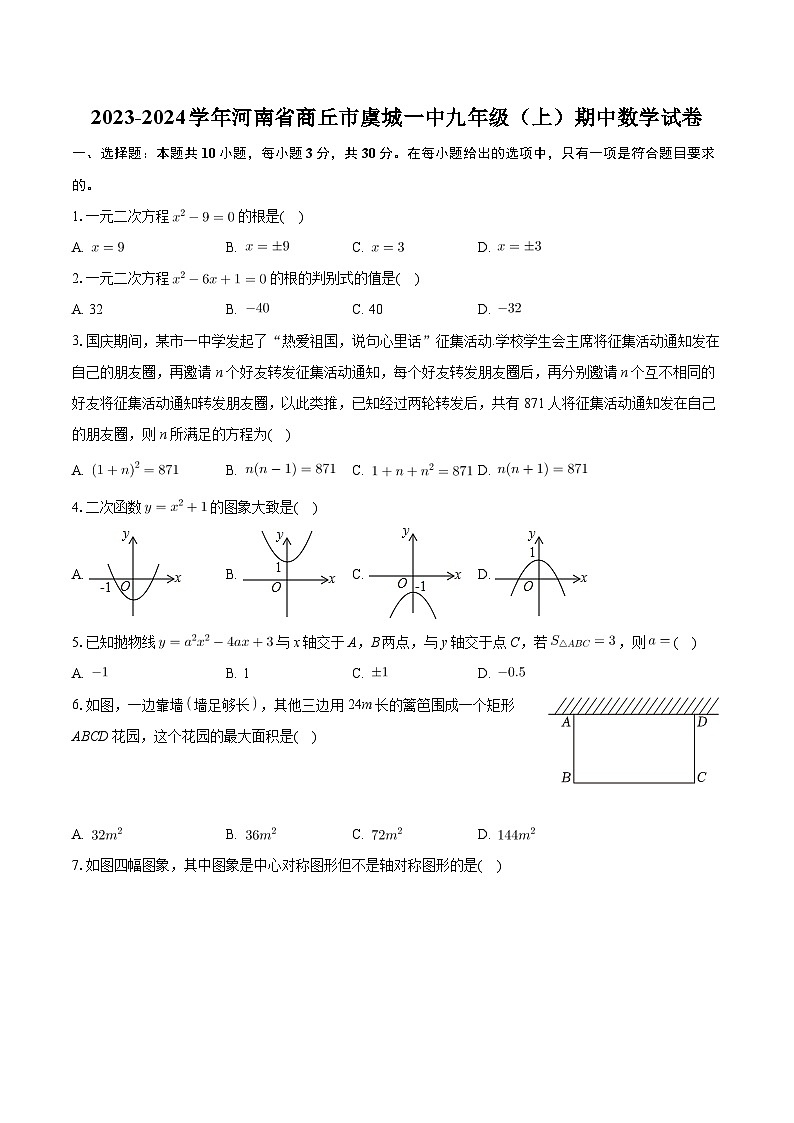
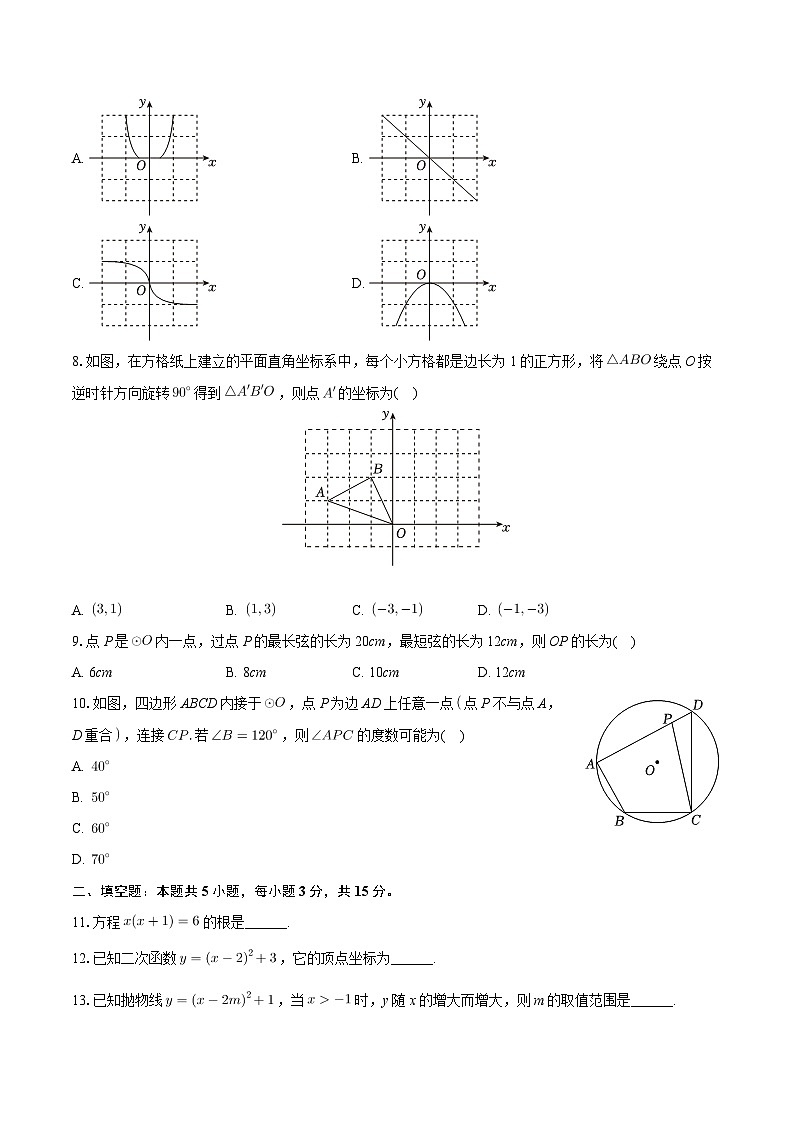
河南省商丘市虞城县第一初级中学2023-2024学年九年级上学期期中数学试卷

这是一份河南省商丘市虞城县第一初级中学2023-2024学年九年级上学期期中数学试卷，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.一元二次方程的根是( )
A. B. C. D.
2.一元二次方程的根的判别式的值是( )
A. 32B. C. 40D.
3.国庆期间，某市一中学发起了“热爱祖国，说句心里话”征集活动.学校学生会主席将征集活动通知发在自己的朋友圈，再邀请n个好友转发征集活动通知，每个好友转发朋友圈后，再分别邀请n个互不相同的好友将征集活动通知转发朋友圈，以此类推，已知经过两轮转发后，共有871人将征集活动通知发在自己的朋友圈，则n所满足的方程为( )
A. B. C. D.
4.二次函数的图象大致是( )
A. B. C. D.
5.已知抛物线与x轴交于A，B两点，与y轴交于点C，若，则( )
A. B. 1C. D.
6.如图，一边靠墙墙足够长，其他三边用24m长的篱笆围成一个矩形ABCD花园，这个花园的最大面积是( )
A. B. C. D.
7.如图四幅图象，其中图象是中心对称图形但不是轴对称图形的是( )
A. B.
C. D.
8.如图，在方格纸上建立的平面直角坐标系中，每个小方格都是边长为1的正方形，将绕点O按逆时针方向旋转得到，则点的坐标为( )
A. B. C. D.
9.点P是内一点，过点P的最长弦的长为20cm，最短弦的长为12cm，则OP的长为( )
A. 6cmB. 8cmC. 10cmD. 12cm
10.如图，四边形ABCD内接于，点P为边AD上任意一点点P不与点A，D重合，连接若，则的度数可能为( )
A.
B.
C.
D.
二、填空题：本题共5小题，每小题3分，共15分。
11.方程的根是______.
12.已知二次函数，它的顶点坐标为______.
13.已知抛物线，当时，y随x的增大而增大，则m的取值范围是______.
14.如图，和关于点C成中心对称，若，，，则AE的长是______.
15.如图，点C，D在以AB为直径的半圆O上，且，点E是上任意一点，连接BE，CE，则的度数为______.
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.本小题16分
用适当的方法解下列方程：
；
；
；
17.本小题6分
一个二次函数的图象经过点和，最小值为求这个二次函数的解析式.
18.本小题8分
在同一坐标系下，一次函数的图象过抛物线上横坐标为1的点.
求b的值；
抛物线的对称轴与这个一次函数图象的交点记为求点P到坐标原点O的距离.
19.本小题8分
宾馆有70个房间供游客居住，当每房间每天定价为180元时，宾馆会住满，每房间每天的定价每增加10元，就会空闲一间房.如果有游客居住，宾馆需对居住的每房间每天支出20元的费用，空闲的房间支出为0元.宾馆经理规定每房间每天定价调整幅度为整十元.
若宾馆经理将每个房间每天定价为x元时，宾馆每天收入记为y元，写出y关于x的函数关系式；
宾馆每天收入能否超过18000元？若能，求出每个房间每天定价是多少元；若不能，请说明理由.
20.本小题8分
如图，AB为的弦，半径OC，OD分别交AB于点E，F，且
求证：
作半径于点M，若，，求OM的长.
21.本小题9分
如图，AB是的直径，C是的中点，于点E，BD交CE于点
求证：
若，，求的半径和CE的长.
22.本小题9分
如图，的顶点坐标分别为、
以点O为旋转中心，将顺时针旋转得到，请画出；
分别写出三个顶点的坐标；
以点A为旋转中心，将逆时针旋转得到直接写出直线的函数解析式.
23.本小题11分
已知抛物线与轴交于A，B两点点A在点B左侧
当时，求y的取值范围；
点P为抛物线上一点，若，求出点P的坐标.
答案和解析
1.【答案】D
【解析】解：，
移项得：，
两边直接开平方得：，
故选：
首先把移到方程的右边，然后两边直接开平方即可．
此题主要考查了直接开平方法解一元二次方程，解这类问题要移项，把所含未知数的项移到等号的左边，把常数项移到等号的右边，化成的形式，利用数的开方直接求解．
2.【答案】A
【解析】解：方程，，，，
，
故选：
根据一元二次方程根的判别式解答即可．
本题考查的是一元二次方程根的判别式，熟知一元二次方程的根与有如下关系：当时，方程有两个不相等的两个实数根；当时，方程有两个相等的两个实数根；当时，方程无实数根是解题的关键．
3.【答案】C
【解析】解：由题意知，第一轮结束后共有个人，第二轮结束后共有个人，
依题意得，，
故选：
由题意知，第一轮结束后共有个人，第二轮结束后共有个人，然后列方程，判断作答即可．
本题考查了由实际问题抽象出一元二次方程．根据题意正确的列方程是解题的关键．
4.【答案】B
【解析】解：二次函数中，
，图象开口向上，顶点坐标为，
符合条件的图象是
故选：
利用二次函数的开口方向和顶点坐标，结合图象找出答案即可．
此题考查二次函数的图象，掌握二次函数的性质，图象的开口方向和顶点坐标是解决问题的关键．
5.【答案】C
【解析】解：对于抛物线，令，即有，
，
解得，，
，B两点的坐标为，，
对于抛物线，令，则有，
点C坐标为，
又，
，
，
，
，经检验，是该方程的解．
故选：
首先确定点A，B，C的坐标，然后结合列出绝对值方程并求解，即可获得答案．
本题主要考查了坐标与图形、二次函数图象与坐标轴交点、绝对值方程以及分式方程等知识，正确确定点A，B，C的坐标是解题关键．
6.【答案】C
【解析】解：设矩形的宽为x m，面积为，根据题意得：
，
时，菜园面积最大，最大面积是
故选：
设矩形的宽为x m，根据矩形的面积公式即可求出函数关系式，再利用配方法求出函数最值．
本题考查二次函数的应用，关键在于找出等量关系列出函数解析式．
7.【答案】C
【解析】解：A、是轴对称图形，不是中心对称图形，故A选项不合题意；
B、既是轴对称图形又是中心对称图形，故B选项不符合题意；
C、不是轴对称图形，是中心对称图形，故C选项符合题意；
D、不是中心对称图形，是轴对称图形，故D选项不合题意．
故选：
根据轴对称图形和中心对称图形的定义：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；中心对称图形的定义：把一个图形绕着某一个点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心，进行逐一判断即可．
此题主要考查了轴对称图形和中心对称图形，解题的关键在于能够熟练掌握轴对称图形和中心对称图形的定义．
8.【答案】D
【解析】解：，
根据旋转的性质得：点的坐标为，
故选：
根据旋转的性质，得到即可得解．
本题考查了坐标与图形变化-旋转，解答本题的关键是熟练掌握旋转的性质．
9.【答案】B
【解析】解：如图，于点P，
由题意可知，过点P的最长弦的长为直径，最短弦的长为，
则，
，
在中，根据勾股定理得：，
故选：
根据直径是圆中最长的弦，可知过点P的最长弦的长为直径，最短弦的长为，即是过点P且垂直于过点P的直径的弦，再根据垂径定理求得CP的长，然后根据勾股定理即可求得OP的长．
本题考查的是垂径定理及勾股定理等知识，熟练掌握垂径定理和勾股定理是解答本题的关键．
10.【答案】D
【解析】解：四边形ABCD内接于，
，
，
，
是的一个外角，
，
的度数可能为，
故选：
根据圆内接四边形的对角互补，求出，根据三角形的外角，得到，判断即可．
本题考查的是圆内接四边形的性质，熟记圆内接四边形的对角互补是解题的关键．
11.【答案】或
【解析】解：，
，
，
则或
或，
故答案为：或
常用的方法由直接开平方法、配方法、因式分解法、求根公式法，
本题考查了一元二次方程的解法，灵活选择合适的方法是解答本题的关键．
12.【答案】
【解析】解：
二次函数，
顶点坐标为，
故答案为：
由抛物线的顶点式即可求得答案．
本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在中，顶点坐标为，对称轴为
13.【答案】
【解析】解：抛物线解析式为，
对称轴为，
又，
抛物线开口向上，
该抛物线的图象在对称轴右侧y随x的增大而增大，
当时，y随x的增大而增大，
，
解得
故答案为：
先求得抛物线的对称轴，再由条件可求得关于m的不等式，求解即可得答案．
此题主要考查了二次函数的图象与系数的关系，根据二次函数解析式得出对称轴为是解题关键．
14.【答案】
【解析】解：与关于点C成中心对称，
≌，
，，，
由勾股定理得：
故答案为：
根据中心对称的性质及，由勾股定理可求得AE的长．
本题考查了中心对称的性质，勾股定理等知识，解题的关键是对中心对称性质的应用．
15.【答案】
【解析】解：连接AC，
是半圆的直径，
，
四边形ABCD是圆内接四边形，
，
，
，
，
故答案为：
连接AC，由圆周角定理得到，由圆内接四边形的性质求出的度数，由直角三角形的性质求出的度数，即可得到的度数．
本题考查圆周角定理，圆内接四边形的性质，掌握圆周角定理，圆内接四边形的性质是解题的关键．
16.【答案】解：，
，
，
，；
方程化为，
，
或，
，；
，
，
，
即，
或，
，；
，
令，
则有，
，
或，
或6，
即或6，
，
【解析】利用直接开平方法解方程即可；
先化为一般式，再利用因式分解法解方程即可；
利用因式分解法解方程即可；
利用换元法和因式分解法解方程即可．
本题主要考查了解一元二次方程，注意，解一元二次方程常用的方法有：直接开平方法，公式法，配方法，因式分解法等．
17.【答案】解：对称轴是AB的垂直平分线，
对称轴为直线
顶点为
设所求解析式为，
将A的坐标代入，得：
，
解得：，
这个二次函数的解析式为
【解析】依据题意，首先求出对称轴为直线，再设所求解析式为，将A的坐标代入，即可求解．
本题主要考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、二次函数的最值，解题时要熟练掌握并能灵活运用二次函数的性质是关键．
18.【答案】解：由题意，将代入，得，
的图象过点，
将代入，得，
由知，一次函数得，
抛物线的对称轴是直线，
将代入得，
点P的坐标是，

【解析】先求出上横坐标为1的点的坐标，再将此坐标代入，即可得答案；
先求出抛物线的对称轴是直线，再求出点P的坐标是，最后根据勾股定理即可求出OP的长．
本题主要考查了一次函数和二次函数的性质，交点坐标，勾股定理，解题的关键是求一次函数和二次函数的交点坐标．
19.【答案】解：房间定价为x元时，空闲的房间数为个，住客房间个数为
，即；
能；
，
当时，，
解得：，，
，
抛物线的开口向下，
当时，
【解析】根据定价，得到游客居住的房间数为，再利用定价乘以居住的房间数减去每间房的支出乘以居住的房间数，列出函数关系式即可；
求出利润等于18000元时的x的值，根据二次函数的性质，进行求解判断即可．
本题考查二次函数的实际应用．
读懂题意，正确的列出函数关系式，是解题的关键．
20.【答案】证明：连接OA、OB，
，
，
，
，
在和中，
，
≌，
；
解：连接OA，如图，
设，则，
于点M，
，，
，
在中，有，
解得

【解析】连接OA、OB，根据题意可证得≌，根据全等三角形的性质证得结论；
连接OA，设，则，在中，由勾股定理得出方程，解方程即可．
本题考查了圆心角、弧、弦的关系、垂径定理以及勾股定理，解题的关键是熟练掌握相关的定理并灵活运用．
21.【答案】证明：是的直径，
，
，
，
，
，
是C是的中点，
，
，
，
；
解：由知，，
，
，，
，
的半径为，
，

【解析】由圆周角定理得，则，进而证明，再由圆周角定理得，则，然后由等腰三角形的判定即可得出结论；
由知，则，再由勾股定理得，则的半径为，然后由三角形面积求出CE的长即可．
本题考查了圆周角定理，圆心角、弧、弦之间的关系，等腰三角形的判定以及勾股定理等知识，熟练掌握圆周角定理是解题的关键．
22.【答案】解：如图，即为所作：
由图可得，；
点B旋转到点C的位置，
，
点C旋转后，在A的左边2个单位，上边一个单位，
而，
，
设直线的函数解析式为，
把，代入，得：
，
解得，，
所以，的函数解析式为
【解析】利用网格特点和旋转的性质画出A、B、C的对应点、、，然后再顺次连接即可；
根据三个顶点在坐标系中的位置可写出三个顶点的坐标即可；
利用旋转变换的性质分别作出A、B、C的对应点，，，再运用待定系数法求出的函数解析式即可．
本题主要考查了旋转作图，运用待定系数法求一次函数解析式，解题的关键是掌握待定系数求一次函数解析式．
23.【答案】解：的对称轴是直线
将代入得
而时，时
的取值范围是
令，得或，
，
，
或
在中令得，即
，方程无解．
在中，令，得，
，
点P的坐标是或
【解析】首先将抛物线配成顶点式，然后根据x的取值范围，从而得出y的取值范围；
根据题意得出AB的长度，然后根据面积求出点P的纵坐标，根据抛物线的解析式求出点P的坐标．
本题主要考查了二次函数的性质、三角形的面积等知识，解题的关键是学会用分类讨论的思想思考问题．