新高考数学概率统计分章节特训专题13超几何分布专题练习(原卷版+解析)

这是一份新高考数学概率统计分章节特训专题13超几何分布专题练习(原卷版+解析)，共10页。
例2．有6个大小相同的黑球，编号为1，2，3，4，5，6，还有4个同样大小的白球，编号为7，8，9，10，现从中任取4个球，有如下几种变量：①表示取出的最大号码；②表示取出的最小号码；③取出一个黑球记2分，取出一个白球记1分，表示取出的4个球的总得分；④表示取出的黑球个数，这四种变量中服从超几何分布的是
A．①②B．③④C．①②④D．①②③④
例3．在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用表示这10个村庄中交通不方便的村庄数，则 ．（用数字表示）
例4．有一批产品，其中有6件正品和4件次品，从中任取3件，至少有2件次品的概率为 ．
例5．设袋中有8个红球，2个白球，若从袋中任取4个球，则其中恰有3个红球的概率为 ．
例6．在10件产品中有2件次品，任意抽取3件，则抽到次品个数的数学期望的值是 ．
例7．在箱子中有10个小球，其中有3个红球，3个白球，4个黑球．从这10个球中任取3个．求：
（1）取出的3个球中红球的个数的分布列；
（2）取出的3个球中红球个数多于白球个数的概率．
例8．某班组织知识竞赛，已知题目共有10道，随机抽取3道让某人回答，规定至少要答对其中2道才能通过初试，他只能答对其中6道，试求：
（1）抽到他能答对题目数的分布列；
（2）他能通过初试的概率．
例9．某校高二年级某班的数学课外活动小组有6名男生，4名女生，从中选出4人参加数学竞赛考试，用表示其中男生的人数，
（1）请列出的分布列；
（2）根据你所列的分布列求选出的4人中至少有3名男生的概率．
例10．某批产品共10件，已知从该批产品中任取1件，则取到的是次品的概率为．若从该批产品中任意抽取3件，
（1）求取出的3件产品中恰好有一件次品的概率；
（2）求取出的3件产品中次品的件数的概率分布列与期望．
例11．生产方提供50箱的一批产品，其中有2箱不合格产品．采购方接收该批产品的准则是：从该批产品中任取5箱产品进行检测，若至多有1箱不合格产品，便接收该批产品．问：该批产品被接收的概率是多少？
例12．甲与乙两人掷硬币，甲用一枚硬币掷3次，记下国徽面朝上的次数为；乙用一枚硬币掷2次，记下国徽面朝上的次数为．
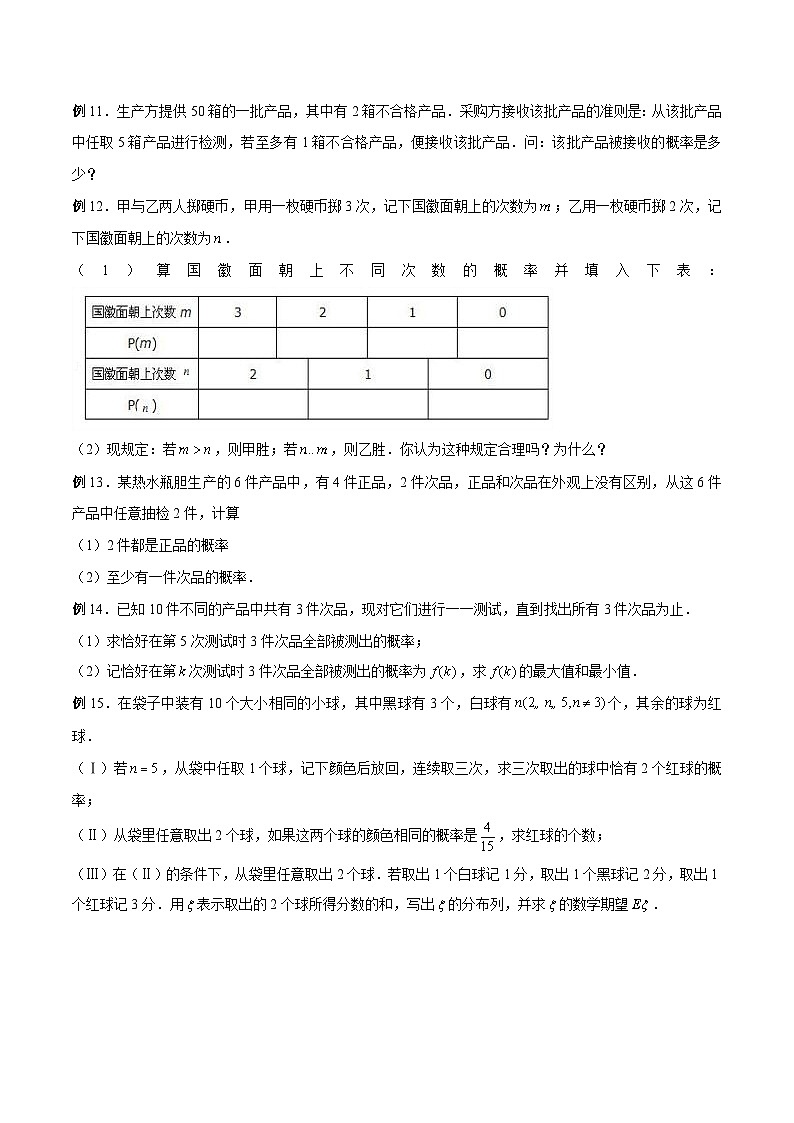
（1）算国徽面朝上不同次数的概率并填入下表：
（2）现规定：若，则甲胜；若，则乙胜．你认为这种规定合理吗？为什么？
例13．某热水瓶胆生产的6件产品中，有4件正品，2件次品，正品和次品在外观上没有区别，从这6件产品中任意抽检2件，计算
（1）2件都是正品的概率
（2）至少有一件次品的概率．
例14．已知10件不同的产品中共有3件次品，现对它们进行一一测试，直到找出所有3件次品为止．
（1）求恰好在第5次测试时3件次品全部被测出的概率；
（2）记恰好在第次测试时3件次品全部被测出的概率为，求的最大值和最小值．
例15．在袋子中装有10个大小相同的小球，其中黑球有3个，白球有个，其余的球为红球．
（Ⅰ）若，从袋中任取1个球，记下颜色后放回，连续取三次，求三次取出的球中恰有2个红球的概率；
（Ⅱ）从袋里任意取出2个球，如果这两个球的颜色相同的概率是，求红球的个数；
（Ⅲ）在（Ⅱ）的条件下，从袋里任意取出2个球．若取出1个白球记1分，取出1个黑球记2分，取出1个红球记3分．用表示取出的2个球所得分数的和，写出的分布列，并求的数学期望．
专题13 超几何分布
例1．有件产品，其中有件次品，从中不放回地抽件产品，抽到的次品数的数学期望值是
A．B．C．D．
【解析】解：设抽到的次品数为，
则有件产品，其中有件次品，从中不放回地抽 件产品，抽到的次品数服从超几何分布即，，，
抽到的次品数的数学期望值
故选：．
例2．有6个大小相同的黑球，编号为1，2，3，4，5，6，还有4个同样大小的白球，编号为7，8，9，10，现从中任取4个球，有如下几种变量：①表示取出的最大号码；②表示取出的最小号码；③取出一个黑球记2分，取出一个白球记1分，表示取出的4个球的总得分；④表示取出的黑球个数，这四种变量中服从超几何分布的是
A．①②B．③④C．①②④D．①②③④
【解析】解：超几何分布取出某个对象的结果数不定，也就是说超几何分布的随机变量为实验次数，即指某事件发生次的试验次数，由此可知③④服从超几何分布．
故选：．
例3．在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用表示这10个村庄中交通不方便的村庄数，则 ．（用数字表示）
【解析】解：由题意
故答案为：
例4．有一批产品，其中有6件正品和4件次品，从中任取3件，至少有2件次品的概率为 ．
【解析】解：从10件产品任取3件的取法共有，其中所取的三件中“至少有2件次品”包括2件次品、3件次品，取法分别为，．
因此所求的概率．
故答案为．
例5．设袋中有8个红球，2个白球，若从袋中任取4个球，则其中恰有3个红球的概率为 ．
【解析】解：从袋中10个球中任取4个球，共有种取法，则其中恰有3个红球的取法为．
从袋中任取4个球，则其中恰有3个红球的概率．
故答案为．
例6．在10件产品中有2件次品，任意抽取3件，则抽到次品个数的数学期望的值是 ．
【解析】解：设抽到次品个数为，则，2，
故答案为：
例7．在箱子中有10个小球，其中有3个红球，3个白球，4个黑球．从这10个球中任取3个．求：
（1）取出的3个球中红球的个数的分布列；
（2）取出的3个球中红球个数多于白球个数的概率．
【解析】解：（1）由题意知，随机变量的所有可能取值为0，1，2，3，
且服从参数为，，的超几何分布，
因此；（1分）
所以，
，
，
；（4分）
所以的分布列为：
（6分）
（2）设“取出的3个球中红球个数多于白球个数”为事件，“恰好取出1个红球和2个黑球”
为事件，“恰好取出2个红球”为事件，“恰好取出3个红球”为事件，（7分）
由于事件，，彼此互斥，且，
而，
，
，（10分）
所以取出的3个球中红球个数多于白球个数的概率为：
．（11分）
答：取出的3个球中红球个数多于白球个数的概率为．（12分）
例8．某班组织知识竞赛，已知题目共有10道，随机抽取3道让某人回答，规定至少要答对其中2道才能通过初试，他只能答对其中6道，试求：
（1）抽到他能答对题目数的分布列；
（2）他能通过初试的概率．
【解析】解：（1）设随机抽出的三道题目某人能答对的道数为，且、1、2、3，服从超几何分布，
分布列如下：
即
（2）要答对其中2道才能通过初试，则可以通过初试包括两种情况，
这两种情况是互斥的，根据上一问的计算可以得到
例9．某校高二年级某班的数学课外活动小组有6名男生，4名女生，从中选出4人参加数学竞赛考试，用表示其中男生的人数，
（1）请列出的分布列；
（2）根据你所列的分布列求选出的4人中至少有3名男生的概率．
【解析】解：（1）依题意得，随机变量服从超几何分布，
随机变量表示其中男生的人数，可能取的值为0，1，2，3，4．
．
所以的分布列为：
（2）由分布列可知至少选3名男生，
即．
例10．某批产品共10件，已知从该批产品中任取1件，则取到的是次品的概率为．若从该批产品中任意抽取3件，
（1）求取出的3件产品中恰好有一件次品的概率；
（2）求取出的3件产品中次品的件数的概率分布列与期望．
【解析】解：设该批产品中次品有件，由已知，
（2分）
（1）设取出的3件产品中次品的件数为，3件产品中恰好有一件次品的概率为（4分）
（2）可能为0，1，2
（10分）
的分布为：
则（13分）
例11．生产方提供50箱的一批产品，其中有2箱不合格产品．采购方接收该批产品的准则是：从该批产品中任取5箱产品进行检测，若至多有1箱不合格产品，便接收该批产品．问：该批产品被接收的概率是多少？
【解析】解：以50箱为一批产品，从中随机抽取5箱，用表示“5箱中不合格产品的箱数”，则服从超几何分布，2，．
这批产品被接收的条件是5箱中没有不合格的箱或只有1箱不合格，
所以被接收的概率为，即．
答：该批产品被接收的概率是．
例12．甲与乙两人掷硬币，甲用一枚硬币掷3次，记下国徽面朝上的次数为；乙用一枚硬币掷2次，记下国徽面朝上的次数为．
（1）算国徽面朝上不同次数的概率并填入下表：
（2）现规定：若，则甲胜；若，则乙胜．你认为这种规定合理吗？为什么？
【解析】解：（1）根据相互独立事件概率乘法公式得：
（2）这种规定是合理的．这是因为甲获胜，则
当时，，1，0，其概率为
当时，，0，其概率为；
当时，，其概率为；
甲获胜的概率为
若乙获胜，则
当时，，1，0，其概率为；
当时，，0，其概率为；
当时，，其概率为；
乙获胜的概率为
甲和乙获胜的概率相等，即获胜机会相等，所以这种规定是合理的．
例13．某热水瓶胆生产的6件产品中，有4件正品，2件次品，正品和次品在外观上没有区别，从这6件产品中任意抽检2件，计算
（1）2件都是正品的概率
（2）至少有一件次品的概率．
【解析】解：从6件产品中，抽取2件的概率有种
（1）其中两件都是正品的基本事件有：种
故2件都是正品的概率
（2）由于“抽检的2件产品中有次品”与“2件都是正品”为对立事件
故抽检的2件产品中至少有一件次品的概率
即至少有一件次品的概率．
例14．已知10件不同的产品中共有3件次品，现对它们进行一一测试，直到找出所有3件次品为止．
（1）求恰好在第5次测试时3件次品全部被测出的概率；
（2）记恰好在第次测试时3件次品全部被测出的概率为，求的最大值和最小值．
【解析】解：（1）若恰好在第5次测试时3件次品全部被测出，则第5次取出第3件次品，前4次中有2次是次品，2次是正品；
则有种情况，从10件产品中顺序取出5件，有种情况，
则第5次测试时3件次品全部被测出的概率，
（2）根据题意，分析可得的范围是，
当时，若恰好在第次测试时3件次品全部被测出，则第次取出第3件次品，前次中有2次是次品，次是正品；而从10件产品中顺序取出件，有种情况，则，
则（3），（4），（5），（6）；
当时，即恰好在第7次测试时3件次品全部被测出，有两种情况，一是第7次取出第3件次品，前6次中有2次是次品，4次是正品；二是前7次没有取出次品，此时也可以测出三件次品，
则；
当时，即恰好在第8次测试时3件次品全部被测出，有两种情况，一是第8次取出第3件次品，前7次中有2次是次品，5次是正品；二是前7次恰有一次次品，第8次取出为合格品，
则；
当时，即恰好在第9次测试时3件次品全部被测出，
此时（9）（3）（4）（5）（6）（7）（8）
故，．
例15．在袋子中装有10个大小相同的小球，其中黑球有3个，白球有个，其余的球为红球．
（Ⅰ）若，从袋中任取1个球，记下颜色后放回，连续取三次，求三次取出的球中恰有2个红球的概率；
（Ⅱ）从袋里任意取出2个球，如果这两个球的颜色相同的概率是，求红球的个数；
（Ⅲ）在（Ⅱ）的条件下，从袋里任意取出2个球．若取出1个白球记1分，取出1个黑球记2分，取出1个红球记3分．用表示取出的2个球所得分数的和，写出的分布列，并求的数学期望．
【解析】解：（Ⅰ）设“从袋中任取1个球是红球”为事件，则．
所以，．
答：三次取球中恰有2个红球的概率为．（4分）
（Ⅱ）设“从袋里任意取出2个球，球的颜色相同”为事件，则，
整理得：，解得（舍或．
所以，红球的个数为3个．（8分）
（Ⅲ）的取值为2，3，4，5，6，且，，，，．
所以的分布列为
所以，．（13分）
0
1
2
3
0
1
2
3
0
1
2
3
0
1
2
3
4
0
1
2
2
3
4
5
6