安徽省宣城市第六中学2024年数学九上开学质量检测模拟试题【含答案】

这是一份安徽省宣城市第六中学2024年数学九上开学质量检测模拟试题【含答案】，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）矩形的面积为,一边长为，则另一边长为（ ）
A．B．C．D．
2、（4分）一元二次方程配方后可化为（ ）
A．B．C．D．
3、（4分）如图，在中，，是的中点，，，若，，
①四边形是平行四边形；
②是等腰三角形；
③四边形的周长是；
④四边形的面积是1．
则以上结论正确的是
A．①②③B．①②④C．①③④D．②④
4、（4分）若一个多边形的内角和小于其外角和,则这个多边形的边数是（ ）
A．3B．4C．5D．6
5、（4分）下列事件中，必然事件是（ ）
A．“奉贤人都爱吃鼎丰腐乳”
B．“2018年上海中考，小明数学考试成绩是满分150分”
C．“10只鸟关在3个笼子里，至少有一只笼子关的鸟超过3只”
D．“在一副扑克牌中任意抽10张牌，其中有5张A”
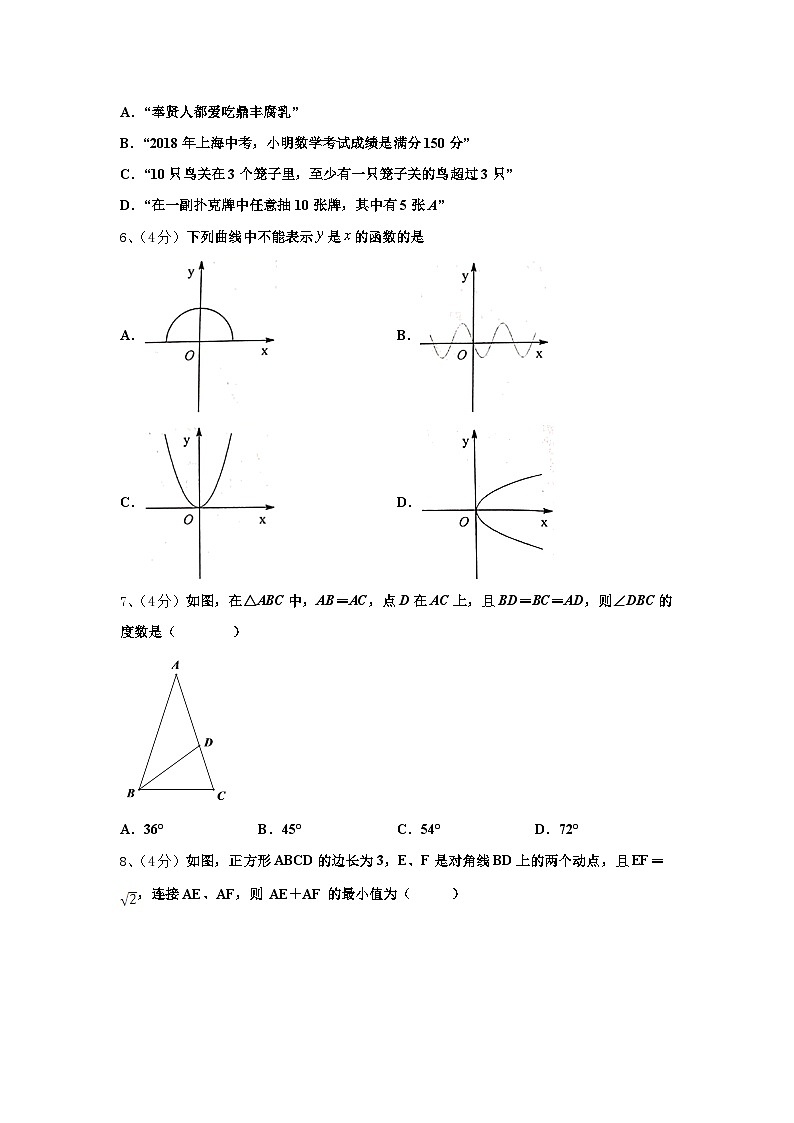
6、（4分）下列曲线中不能表示是的函数的是
A．B．
C．D．
7、（4分）如图，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，则∠DBC的度数是（ ）
A．36°B．45°C．54°D．72°
8、（4分）如图，正方形ABCD的边长为3，E、F是对角线BD上的两个动点，且EF＝，连接AE、AF，则 AE＋AF 的最小值为（ ）
A．B．3C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）某初中校女子排球队队员的年龄分布：
该校女子排球队队员的平均年龄是_____岁．（结果精确到0.1）
10、（4分）把直线y＝﹣x﹣3向上平移m个单位，与直线y＝2x+4的交点在第二象限，则m的取值范围是_____．
11、（4分）如图，的面积为36,边cm，矩形DEFG的顶点D、G分别在AB、AC上，EF在BC上，若，则______cm.
12、（4分）分解因式：______________。
13、（4分）已知，化简二次根式的正确结果是_______________．
三、解答题（本大题共5个小题，共48分）
14、（12分）化简：(.
15、（8分）计算
（1）
（2）．
16、（8分）已知方程组，当m为何值时，x＞y？
17、（10分）为营造书香家庭，周末小亮和姐姐一起从家出发去图书馆借书，走了6min发现忘带借书证，小亮立即骑路边共享单车返回家中取借书证，姐姐以原来的速度继续向前走，小亮取回借书证后骑单车原路原速前往图书馆，小亮追上姐姐后用单车带着姐姐一起前往图书馆。已知骑车的速度是步行速度的2倍，如图是小亮和姐姐距离家的路程y(m)与出发的时间x(min)的函数图象，根据图象解答下列问题：
（1）小亮在家停留了多长时间？
（2）求小亮骑车从家出发去图书馆时距家的路程 y(m)与出发时间 x(min)之间的函数解析式.
18、（10分）如图，已知□ABCD中，AE平分∠BAD，CF平分∠BCD，分别交BC、AD于E、F．求证：AF＝EC．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，在菱形ABCD中，AC、BD交于点O，AC＝6，BD＝8，若DE∥AC，CE∥BD，则OE的长为_____．
20、（4分）如图，在菱形ABCD中，AC=8，BD=6，则△ABC的周长是_____．
21、（4分）比较大小：________.
22、（4分）如图，将沿方向平移得到，如果四边形的周长是，则的周长是____．
23、（4分）已知 ，，则=______。
二、解答题（本大题共3个小题，共30分）
24、（8分）计算：
(1)
(2)
25、（10分）如图所示，平行四边形中，和的平分线交于边上一点 ，
(1)求的度数.
(2)若，则平行四边形的周长是多少?
26、（12分）如图，在中，点，分别在，上，且，连结、．
求证：．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据矩形的面积得出另一边为，再根据二次根式的运算法则进行化简即可．
【详解】
∵矩形的面积为18，一边长为，
∴另一边长为，
故选：C．
本题考查了矩形的面积和二次根式的除法，能根据二次根式的运算法则进行化简是解此题的关键．
2、D
【解析】
配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．
【详解】
解：
故选：D．
本题考查一元二次方程的配方法，解题的关键是熟练运用配方法，本题属于基础题型．
3、A
【解析】
证明AC∥DE，再由条件CE∥AD可证明四边形ACED是平行四边形；根据线段的垂直平分线证明AE=EB可得△BCE是等腰三角形；首先利用三角函数计算出AD=4，CD=2，再算出AB长可得四边形ACEB的周长是10+2，利用△ACB和△CBE的面积和可得四边形ACEB的面积．
【详解】
①，，
，
，
，
四边形是平行四边形，故①正确；
②是的中点，，
，
是等腰三角形，故②正确；
③，，
，，
四边形是平行四边形，
，
，
，，
，
，
四边形的周长是故③正确；
④四边形的面积：，故④错误，
故选．
此题主要考查了平行四边形的判定和性质，以及三角函数的应用，关键是利用三角函数值计算出CB长．
4、A
【解析】
试题分析：∵多边形的外角和是360度，多边形的内角和等于它的外角和，则内角和是360度，
∴这个多边形是四边形．
故选B．
考点：多边形内角与外角．
5、C
【解析】
根据事件发生的可能性大小判断相应事件的类型即可.
【详解】
解：A、“奉贤人都爱吃鼎丰腐乳”是随机事件；
B、“2018年上海中考，小明数学考试成绩是满分150分”是随机事件；
C、“10只鸟关在3个笼子里，至少有一只笼子关的鸟超过3只”是必然事件；
D、“在一副扑克牌中任意抽10张牌，其中有5张A”是不可能事件.
故选C.
本题考查了事件发生的可能性大小的判断.
6、D
【解析】
根据函数的定义即可判断.
【详解】
因为是的函数时，只能一个x对应一个y值，故D错误.
此题主要考查函数的定义，解题的关键是熟知函数图像的性质.
7、A
【解析】
由已知条件开始，通过线段相等，得到角相等，再由三角形内角和求出各个角的大小．
【详解】
解：设∠A＝x°，
∵BD＝AD，
∴∠A＝∠ABD＝x°，∠BDC＝∠A＋∠ABD＝2x°，
∵BD＝BC，
∴∠BDC＝∠BCD＝2x°，
∵AB＝AC，
∴∠ABC＝∠BCD＝2x°，
在△ABC中x＋2x＋2x＝180，
解得：x＝36，
∴∠C＝∠BDC＝72°，
∴∠DBC＝36°，
故选：A．
此题考查了等腰三角形的性质；熟练掌握等腰三角形的性质，以及三角形内角和定理，得到各角之间的关系式解答本题的关键．
8、A
【解析】
如图作AH∥BD，使得AH=EF=，连接CH交BD于F，则AE+AF的值最小．
【详解】
解：如图作AH∥BD，使得AH=EF=，连接CH交BD于F，则AE+AF的值最小．
∵AH=EF，AH∥EF，
∴四边形EFHA是平行四边形，
∴EA=FH，
∵FA=FC，
∴AE+AF=FH+CF=CH，
∵四边形ABCD是正方形，
∴AC⊥BD，∵AH∥DB，
∴AC⊥AH，
∴∠CAH=90°，
在Rt△CAH中，CH= =2 ，
∴AE+AF的最小值2，
故选：A．
本题考查轴对称-最短问题，正方形的性质、勾股定理、平行四边形的判定和性质等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、14.1．
【解析】
根据加权平均数的计算公式把所有人的年龄数加起来，再除以总人数即可．
【详解】
该校女子排球队队员的平均年龄是≈14.1（岁），
故答案为：14.1．
此题考查了加权平均数，掌握加权平均数的计算公式是解题的关键，是一道基础题．
10、1＜m＜1．
【解析】
直线y＝﹣x﹣3向上平移m个单位后可得：y＝﹣x﹣3+m，求出直线y＝﹣x﹣3+m与直线y＝2x+4的交点，再由此点在第二象限可得出m的取值范围．
【详解】
解：直线y＝﹣x﹣3向上平移m个单位后可得：y＝﹣x﹣3+m，
联立两直线解析式得：，
解得：，
即交点坐标为（，），
∵交点在第二象限，
∴，
解得：1＜m＜1．
故答案为1＜m＜1．
本题考查一次函数图象与几何变换、两直线的交点坐标，注意第二象限的点的横坐标小于2、纵坐标大于2．
11、6
【解析】
作AH⊥BC于H点，可得△ADG∽△ABC，△BDE∽△BAH，根据相似三角形对应边比例等于相似比可解题．
【详解】
解：作AH⊥BC于H点，
∵四边形DEFG为矩形，
∴△ADG∽△ABC，△BDE∽△BAH，
∵的面积为36,边cm
∴AH=6
∵EF=2DE，即DG=2DE
解得：DE=3
∴DG=6
故答案为：6
本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质．
12、4x（x+1）（x-1）
【解析】
4x3-4x=4x(x2-1)=4x(x+1)(x-1).
故答案为4x(x+1)(x-1).
13、
【解析】
由题意：-a3b≥0，即ab≤0，
∵a＜b，
∴a≤0＜b；
所以原式=|a|=-a．
三、解答题（本大题共5个小题，共48分）
14、8-4
【解析】
【分析】运用平方差公式和完全平方公式可求出结果.
【详解】解：原式=2﹣1+3﹣4+4
=8﹣4.
【点睛】本题考核知识点：整式运算.解题关键点：熟记平方差公式和完全平方公式.
15、4+；6+
【解析】
（1）先根据二次根式的乘除法则运算，然后合并即可；
（2）先把各二次根式化为最简二次根式，然后合并即可．
【详解】
解：（1）原式=﹣+2=4﹣+2=4+；
（2）原式=5﹣+﹣1=4+．
考点：二次根式的混合运算
16、．
【解析】
解含有参数m的二元一次方程组，得到关于m的x、y的值，再根据x＞y的关系解不等式求出m的取值范围即可.
【详解】
解：，
②×2﹣①得：x=m﹣3③，
将③代入②得：y=﹣m+5，
∴得，
∵x＞y，
∴m﹣3＞﹣m+5，
解得m＞4，
∴当m＞4时，x＞y．
17、（1）小亮在家停留了1min；（2）.
【解析】
【分析】（1）根据路程与速度、时间的关系，首先求出C、B两点的坐标，即可解决问题；
（2）根据C、D两点坐标，利用待定系数法即可解决问题.
【详解】（1）步行速度：300÷6=50m/min，单车速度：2×50=100m/min，
单车时间：3000÷100=30min，40-30=10，
∴C（10，0），
∴A到B是时间==3min，
∴B（9，0），
∴BC=1，
∴小亮在家停留了1分钟；
(2)设解析式为y=kx+b ,将C (10,0) 和D (40,300) 代入得
，解得，
所以 .
【点睛】本题考查一次函数的应用、路程、速度、时间之间的关系等知识，解题的关键是理解题意，读懂图象信息，灵活运用所学知识解决问题．
18、证明见解析.
【解析】
由四边形ABCD是平行四边形，AE平分∠BAD，CF平分∠BCD，易证得△ABE≌△CDF（ASA），即可得BE=DF，又由AD=BC，即可得AF=CE．
【详解】
证明：∵四边形ABCD是平行四边形，
∴∠B=∠D，AD=BC，AB=CD，∠BAD=∠BCD，
∵AE平分∠BAD，CF平分∠BCD，
∴∠EAB=∠BAD，∠FCD=∠BCD，
∴∠EAB=∠FCD，
在△ABE和△CDF中，
，
∴△ABE≌△CDF（ASA），
∴BE=DF．
∵AD=BC，
∴AF=EC．
本题主要考查平行四边形的性质与判定；证明四边形AECF为平行四边形是解决问题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1
【解析】
根据菱形的性质得出AC⊥BD，由勾股定理可求AD＝CD＝1，再根据平行四边形的判定定理得四边形OCED为平行四边形，由矩形的判定定理得出四边形OCED是矩形，则该矩形的对角线相等，即CD＝OE＝1．
【详解】
证明：∵四边形ABCD为菱形，
∴AC⊥BD，OA＝AC＝3，OD＝BD＝4，
∴∠AOD＝90°，
∴AD＝＝1＝CD
∵DE∥AC，CE∥BD
∴四边形OCED为平行四边形，
又∵AC⊥BD
∴四边形OCED为矩形
∴CD＝OE＝1
故答案为：1
本题考查了矩形的判定以及菱形的性质，还考查了平行四边形的判定，掌握平行四边形的判定方法是解题的关键．
20、18
【解析】
分析：利用菱形的性质结合勾股定理得出AB的长，进而得出答案．
详解：∵在菱形ABCD中，AC=8，BD=6，
∴AB=BC,∠AOB=90°，AO=4，BO=3，
∴BC=AB=，
∴△ABC的周长=AB+BC+AC=5+5+8=18.
故答案为18
点睛：本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.
21、＜
【解析】
试题解析：∵
∴
∴
22、
【解析】
根据平移的性质可得，即可求得的周长．
【详解】
平移，
，
，
，
故答案为：1．
本题考查了三角形平移的问题，掌握平移的性质是解题的关键．
23、60
【解析】
=2ab（a+b），将a+b=3，ab=10，整体带入即可.
【详解】
=2ab（a+b）=2×3×10=60.
本题主要考查利用提公因式法分解因式，整体带入是解决本题的关键.
二、解答题（本大题共3个小题，共30分）
24、（1）；（2）－－.
【解析】
【分析】（1）根据同分母分式加减法的法则进行计算即可得；
（2）利用多项式乘多项式的法则进行展开，然后再合并同类二次根式即可得.
【详解】（1）＝ ＝；
（2）原式＝－＋－
＝－－.
【点睛】本题考查了分式的加减法、二次根式的混合运算，熟练掌握同分母分式加减法法则、二次根式混合运算的运算法则是解题的关键.
25、（1）；（2）平行四边形的周长是.
【解析】
（1）根据∠BEC＝180°﹣（∠EBC+∠ECB），把∠EBC+∠ECB用角平分线定义转化为∠ABC与∠DCB和的一半即可；
（2）根据角平分线和平行线得到AE＝AB，DE＝DC，由此可得平行四边形ABCD周长＝6AB．
【详解】
解:(1) ∵四边形是平行四边形

又∵平分和
.
∴∠BEC＝180°﹣（∠EBC+∠ECB）=90°；
(2)在中，.

又
，同理：
∵平行四边形中，，
∴平行四边形的周长是.
本题主要考查了平行四边形的性质、勾股定理，解题的关键是通过角平分线和平行线转化线段．
26、证明见解析
【解析】
根据平行四边形性质得出AD∥BC，AD=BC，求出DE=BF，DE∥BF，得出四边形DEBF是平行四边形，根据平行四边形的性质推出即可．
【详解】
证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵AE=CF，
∴DE=BF，DE∥BF，
∴四边形DEBF是平行四边形，
∴BE=DF．
本题考查了平行四边形的性质和判定；熟练掌握平行四边形的性质，证明四边形DEBF是平行四边形是解决问题的关键．
题号
一
二
三
四
五
总分
得分
年龄/（岁）
13
14
15
16
频数
1
4
5
2