高中数学人教B版 (2019)选择性必修 第一册2.6.2 双曲线的几何性质教学ppt课件

这是一份高中数学人教B版 (2019)选择性必修 第一册2.6.2 双曲线的几何性质教学ppt课件，共27页。PPT课件主要包含了课程标准，学习目标三等内容，欢迎下载使用。

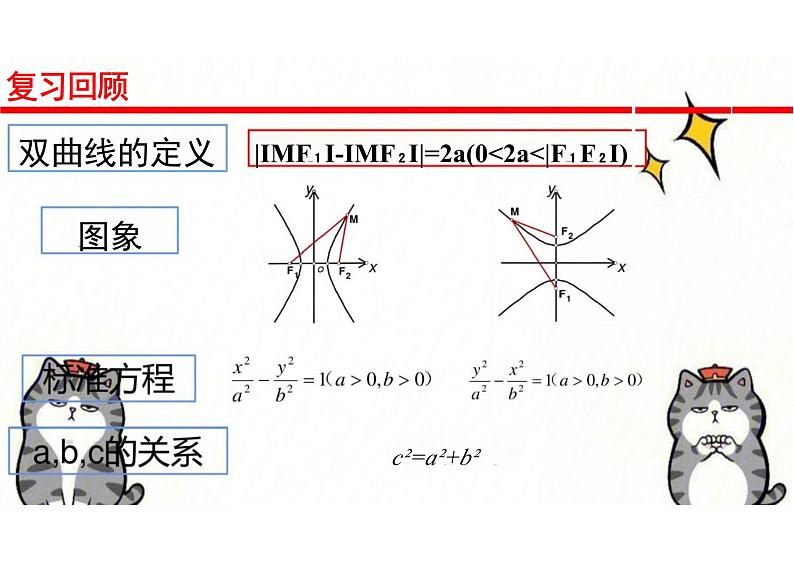
复习回顾双曲线的定义 |IMF₁I-IMF₂I|=2a(0<2a<|F₁F₂I)图象
1.了解双曲线的简单几何性质(范围、对称性、 顶点、实轴长和虚轴长等);2.了解双曲线的渐近线，并能用双曲线的简单几
何性质解决一些简单问题。
理解双曲线离心率的定义、取值范围和渐近线方程. (逻辑推理)通过具体实例初步了解直线与双曲线相交的相 关问题. (数学运算)
重点：双曲线的几何性质，双曲线各元素之间的相互依存 关系，特别是双曲线的渐近线的性质难点：有关双曲线的离心率、渐近线的问题
学习目标掌握双曲线的简单几何性质.(直观想象)
本课导入下面我们由双曲线的方程来研究双曲线具有的几何性质已知双曲线C 的方程为 ,根据这个方程完成下列任务：(1)观察方程中x 与y是否有取值范围，由此指出双曲线C 在平面直角坐标 系中的位置特征；(2)指出双曲线C 是否关于x轴 、y 轴、原点对称；(3)指出双曲线C与坐标轴是否有交点，如果有，求出交点坐标；( 4 ) 如 果(x,y)满足双曲线C 的方程，说出当|x|增大时，|y 将怎样变化，并 指出这反映了双曲线的形状具有什么特点
我们可以根据方程得到双曲线什么样的几何性质呢?
一般地，如果双曲线C 的标准方程是
1 . 范围观察平面直角坐标系中的双曲线，它有怎样的范围?能利用它的方程给出证明吗?
双曲线上点(x,y) 都满所 , 即x²≥a², 所以 |x|≥a(a>0).双曲线在不等式x≥a与x≤-a所表示的区域闲
2 .对称性如果(x,y)是方程①的一组解，则不难看出(-x,y), (x,-y),(-x,-y) 都是方程的解，(x,y)和(x,-y )关于x轴对称，所以双曲线关于x轴对称 (x,y)和(-x,y)关于y轴对称，所以双曲线关于y轴对称(x,y)(y )关于原点对称，所以双曲线关于原点对称 双曲线关干y轴、轴、原点都是对称的.坐标轴是双曲线的对称轴.原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心
在方程①中，令y=0, 得x=±a,双曲线和x轴有两个交点A₁ (-a,0)、A₂ (a,O),叫做双曲线的顶点.令x=0, 得y²=-b²,这个方程没有实数根，则双曲线和y轴无交点.特殊点B₁(0,-b) 、B₂(0,b).
线段A,A₂叫做双曲线的实轴.线段B₁B₂叫做双曲线的虚轴.实轴的长等于2a .虚轴的长等于2b.叫做双曲线的实半轴长.b叫做双曲线的虚半轴长特别的，实轴长与虚轴长相等的双曲线成为等轴双曲线.
由方程可以看出，如果(x,y)是双曲线上一点，则|x|增大时，
ly|也是增大的.这就是说，双曲线向四周无限延展，那么,这种 无限延展还有什么性质呢?考虑到双曲线关于坐标轴和原点对称，因此我们只需了解双 曲线在第一象限内的情况即可。在第一象限内，双曲线的方程可以改写为因为x>a 时， √x2-a²< √x²=x,这说咀在第一象限内，双曲线一定在直线 的下方；又因 为此时如果x越来越大，则√x²-a²≈ √x²=x,双曲线会越来越接近直
第二象限 第三象限
新知讲解从几何直观上来看：双曲线在四个象限，四个方向上无限接近两条直线y=± 但又始终不相交，从代数角度上来看：计算双曲线上的点P(x,y)到渐近线的距离d,对于第一象限：当x→+0,d→0, 但是d≠0无限接近，但又始终不相交，我们把这两条直线叫做双曲线的渐近线双曲线怎样做，才更准确?
5 . 离心率同椭圆的情形一样，双曲线的半焦距与半长轴长之比
(1)根据双曲线离心率的定义，判断双曲线离心率的取值范围；a>0, 所 以e>1.
所以e越趋近于1,b的值越小，双曲线的渐近线所夹的双曲线区域越狭窄.a
(2)猜想双曲线离心率的大小与双曲线的形状有什么联系，并尝
试证明.x²-y²=1
例1.求下列方程表示的双曲线的实轴长、焦点坐标、离解 ：
(2)双曲线的方程可化双曲线的焦点在y轴上，且a²=b²=9,实轴长2a=6.又因为c²=a²+b²=18, 即c=3 √2.因此，双曲线焦点坐标为(0,-3y2,(0,32).渐近线方程为y=±x.
(1)由标准方程知双曲线焦点在x轴上，且a²=9,b²=16,因此实轴长2a=6.因此，双曲线焦点坐标为(-5,0),(5,0).
以及渐近线方程： (2)x²-y²=+.
又因为c²=a²+b²=25, 即c=5.
解 将 9y²—4x²=—36变形 所以a=3,b=2,c=√ 13,因此顶点坐标为(一3,0),(3,0),
延伸探究：求双曲线9y²-4x²=-36 的顶点坐标、焦点长、虚轴长、离心率和渐近线方程.
实轴长是2a=6, 虚轴长是2b=4,渐近线方程
焦标为(- √ 13,0),(N13,0),
反思感悟由双曲线的标准方程求几何性质的一般步骤化标准- 对于非标准形式的双曲线方程要先化成标准形式定位置 根据方程确定焦点在x 轴上还是在y 轴上求参数- 写出a²,b² 的值，由a²+b²=c² 得出c² 的值根据上面所求a,b,c, 由焦点所在的坐标轴得出所写性质- 求的几何性质
解 依题意可知，双曲线的焦点在y轴上，且c=13, 9∴a=5,b²=c²—a²=144,
一个焦点为(0,13),且离心率为
例2 求适合下列条件的双曲线的标准方程：
确时，应注意分类讨论，也可以不分类讨论直接把双曲线方程设成mx²+ny²=1(mn< 0),从而直接求出来.
由双曲线的几何性质求双曲线的标准方程常用待定系数法，当焦点位置明确时直接设出双曲线的标准方程即可；当焦点位置不明
数学思想方法：“类比学习法”和“数形结合法”核心素养：直观想象，逻辑推理，数学运算
1.等轴双曲线的离心率是\2.( √)2.椭圆的离心率与双曲线的离心率取值范围相同. (×)3.双曲 ,b>0) 的渐近线方程为 (×)4.中心在原点，实轴长为10,虚轴长为6的双曲线的标准方程是(B )
课堂作业必 做：P155练习A 第1、3题；练习B第1,2题
选 做 ：P155练习A组2题，练习B组第5题
天才在于积累，聪明在于勤奋 ---华罗庚
(2)渐近线方程为 ,且经过点A(2,-3); 解 ∵ 双曲线的渐近线方程为(1)若焦点在x 轴上，设所求双曲线的标准方程 ∵A(2,—3) 在双曲线上，由①②联立，无解.(2)若焦点在y 轴上，设所求双曲线标准方程市 @, —3)在双曲线上，一由3④联立，解得a²=8,b²=32.∴所求双曲线的标准方程
b>0), 则b>0), 则