陕西省宝鸡市第一中学（高新校区）2024-2025学年九年级上学期第一次月考数学试题

这是一份陕西省宝鸡市第一中学（高新校区）2024-2025学年九年级上学期第一次月考数学试题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
九年级数学
BYZ
（时间120分钟 分值120分）
一、选择题（每题3分，共30分）
1.下列方程中：①；②；③；④.一元二次方程有（ ）
A.1个B.2个C.3个D.4个
2.根据表格对应值：
判断关于x的方程的一个解x的范围是（ ）
A.B.C.D.无法判定
3.顺次连接四边形四边的中点所得的四边形为矩形，则四边形一定满足（ ）
A.B.
C.，D.
4.一元二次方程配方后可化为（ ）
A.B.C.D.
5.关于x的一元二次方程有实数根，则a的取值范围是（ ）
A.且B.C.且D.
6.参加足球联赛的每两队之间都进行两场比赛，共要比赛90场，设共有x个队参加比赛，则下列方程符合题意的是（ ）
A.B.C.D.
7.电影《长津湖》上映以来，全国票房连创佳绩.据不完全统计，某市第一天票房约2亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达18亿元，将增长率记作x，则方程可以列为（ ）
A.B.C.D.
8.如图，一根长5米的梯子斜靠在与地面垂直的墙上，点P为的中点，当梯子的一端A沿墙面向下移动，另一端B沿向右移动时，的长（ ）
A.逐渐增大B.逐渐减小C.不变D.先增大，后减小
9.如图，将矩形对折，使与边重合，得到折痕，再将点A沿过点D的直线折叠到上，对应点为，折痕为，，，则的长度为（ ）
A.B.4C.D.3
10.如图，矩形中，，，点P为对角线上一动点，于点E，于点F，则线段长的最小值为（ ）
A.5B.B.C.D.
二、填空题（每题3分，共15分）
11.方程的一次项系数是__________.
12.如图，某单位准备将院内一块长30m，宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道，剩余的地方种植花草，要使种植花草的面积为532，设小道进出口的宽度为m，根据条件，可列出方程：__________.
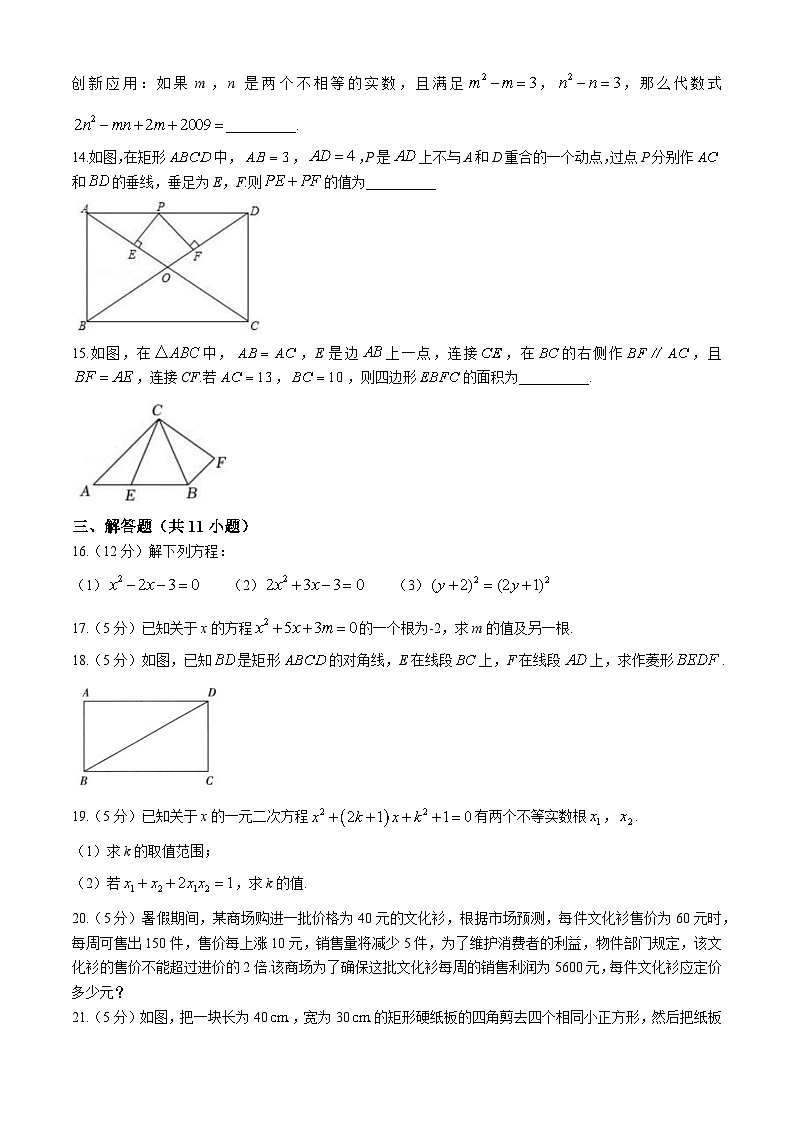
13.阅读材料：如果a，b是一元二次方程的两个实数根，则有，，创新应用：如果m，n是两个不相等的实数，且满足，，那么代数式__________.
14.如图，在矩形中，，，P是上不与A和D重合的一个动点，过点P分别作和的垂线，垂足为E，F.则的值为__________
15.如图，在中，，E是边上一点，连接，在的右侧作，且，连接CF.若，，则四边形的面积为__________.
三、解答题（共11小题）
16.（12分）解下列方程：
（1） （2） （3）
17.（5分）已知关于x的方程的一个根为-2，求m的值及另一根.
18.（5分）如图，已知是矩形的对角线，E在线段上，F在线段上，求作菱形.
19.（5分）已知关于x的一元二次方程有两个不等实数根，.
（1）求k的取值范围；
（2）若，求k的值.
20.（5分）暑假期间，某商场购进一批价格为40元的文化衫，根据市场预测，每件文化衫售价为60元时，每周可售出150件，售价每上涨10元，销售量将减少5件，为了维护消费者的利益，物件部门规定，该文化衫的售价不能超过进价的2倍.该商场为了确保这批文化衫每周的销售利润为5600元，每件文化衫应定价多少元？
21.（5分）如图，把一块长为40，宽为30的矩形硬纸板的四角剪去四个相同小正方形，然后把纸板的四边沿虚线折起，并用胶带粘好，即可做成一个无盖纸盒.若该无盖纸盒的底面积为600，求剪去小正方形的边长.
22.（6分）在矩形中，，对角线与相交于点O，，垂足为E，.求的长.
23.（6分）如图，利用一面墙（墙长25米），用总长度52米的栅栏（图中实线部分）围成一个矩形围栏，且中间共留两个1米的小门，设栅栏长为x米.
（1）_________米（用含x的代数式表示）；
（2）若矩形围栏面积为240平方米，求栅栏的长.
24.（8分）如图所示，在中，，D为的中点，四边形为平行四边形，，相交于F，连接，.
（1）试确定四边形的形状，并说明理由.
（2）当满足什么条件时，四边形为正方形？请给予证明.
25.（8分）如图，已知菱形的边长为2，，点M、N分别是边、上的两个动点，，连接.
（1）是等边三角形吗？如是，请证明；如不是，请说明理由.
（2）在M、N运动的过程中，四边形的面积是否发生变化？若不变化，求出面积的值；若变化，说明理由.
26.（10分）［问题再现］如图（1），正方形的对角线相交于点O，正方形与正方形的边长相等.在正方形绕点O旋转的过程中，两个正方形重叠部分的面积（即四边形的面积）始终等于正方形面积的.

图（1） 图（2） 图（3）
【初步探究】小明在证明上述问题时，发现题目中正方形，这一条件主要用到的信息是，图中一些线段之间也有特殊的关系.深入思考后他为大家编了如下题目：如图（2），中，，，O是边的中点.以O为顶点作，交线段于点E，交线段于点F.请完成以下问题：问题（1）：四边形的面积是面积的__________.
问题（2）：猜想线段、、之间的等量关系，并说明理由.
【延伸探究】爱动脑的小军在小明问题的基础上进行了延伸，让绕点O旋转，交直线于点E，交直线于点F，连接.若，，求的面积.
试卷类型：A
2024—2025学年度第一学期第二次学情调研（卷）
九年级数学
BYZ
一、选择题
BCBCA DDCAB
二、填空题（每题3分，共15分）
11.-3 12. 13.2020 14. 15.60
三、解答题（共11小题）
16.（12分）解下列方程：
（1）
（2），.
（3），.
17.解：设另一根为t，
由根与系数的关系可得，，
解得.
故方程的另一根为–3，m的值为2.
18.
19.∵关于x的一元二次方程有两个不等实数根，，
∴，
∴
（2）根据根与系数的关系，可得，，
又∵，
∴，
解得或，
由（1）得，
∴.
20.解：设每件文化衫的定价为x元，则每周的销售量为件，
依题意，得：，
解得：，.
因为售价不能超过进价的2倍，
所以，
所以不合题意，舍去，
所以.
答：每件文化衫应定价为80元.
21.解：设剪去小正方形的边长是x，则纸盒底面的长为，宽为，
根据题意得：.
整理得：.
解得：（舍去），，
答：剪去小正方形的边长是5.
22.解：∵四边形是矩形，
∴，，，
∴，
∵，
∴，
∵，
∴，
∴，
即是等边三角形，
∴，
∴，
∵，，
∴，
23.解：（1）；
（2）依题意得：，
整理得：，
解得：，.
当时，，不合题意，舍去；
当时，，符合题意.
答：栅栏的长为10米.
的小门，设栅栏长为x米.
24.解：（1）四边形是矩形理由如下，
∵，D为的中点，
∴，，
∴，
∵四边形为平行四边形，
∴，，
，，
∴四边形是平行四边形，
又∵，
∴是矩形；
（2）当时，四边形为正方形，
证明：∵四边形为平行四边形，
∴，
∴，
∵，
∴，
，
∴矩形为正方形.
25.解：（1）是等边三角形，
证明：如图，连接，
∵四边形是菱形，
∴，，
∴，都是等边三角形，
∴，，
∴，
在和中，
∴，
∴，
∴，
∴是等边三角形；
（2）四边形的面积不发生变化，理由如下：
∵，
∴，
∴四边形的面积
∴四边形的面积不发生变化.
26.解：【初步探究】（1）如图，连接，
∵，，O是边的中点，
∴，，，
∴，
∵，
∴，
∴，
在和中，
∴，
∴，
∴.
故答案为：；
（2），
理由如下：连接，
∵，，O是边的中点，
∴，，，
∴，
∵，
∴，
∴，
在和中，
，
∴，
∴，
∴.
【延伸探究】①如图，连接，过O作于点H，
∴，
由（1）知在等腰直角中，，
∵，O是边的中点，
∴，
∴，
∴，，
∴，
∴，
∴，
∴是等腰直角三角形，
∵，
∴，
由勾股定理得：，
∴的面积为；
②如图，作于点P，
同理，
∴，
∴是等腰直角三角形，
∵，
∴，
由勾股定理得：，
∴的面积为：，
综上可知：的面积为或.
x
1.1
1.2
1.3
1.4
–0.59
0.84
2.29
3.76