河北省邯郸市人和中学2024~2025学年八年级上学期第一次月考数学试题

这是一份河北省邯郸市人和中学2024~2025学年八年级上学期第一次月考数学试题，共9页。试卷主要包含了下列图形中，是正八边形的是，下列图形中，与如图全等的是等内容，欢迎下载使用。

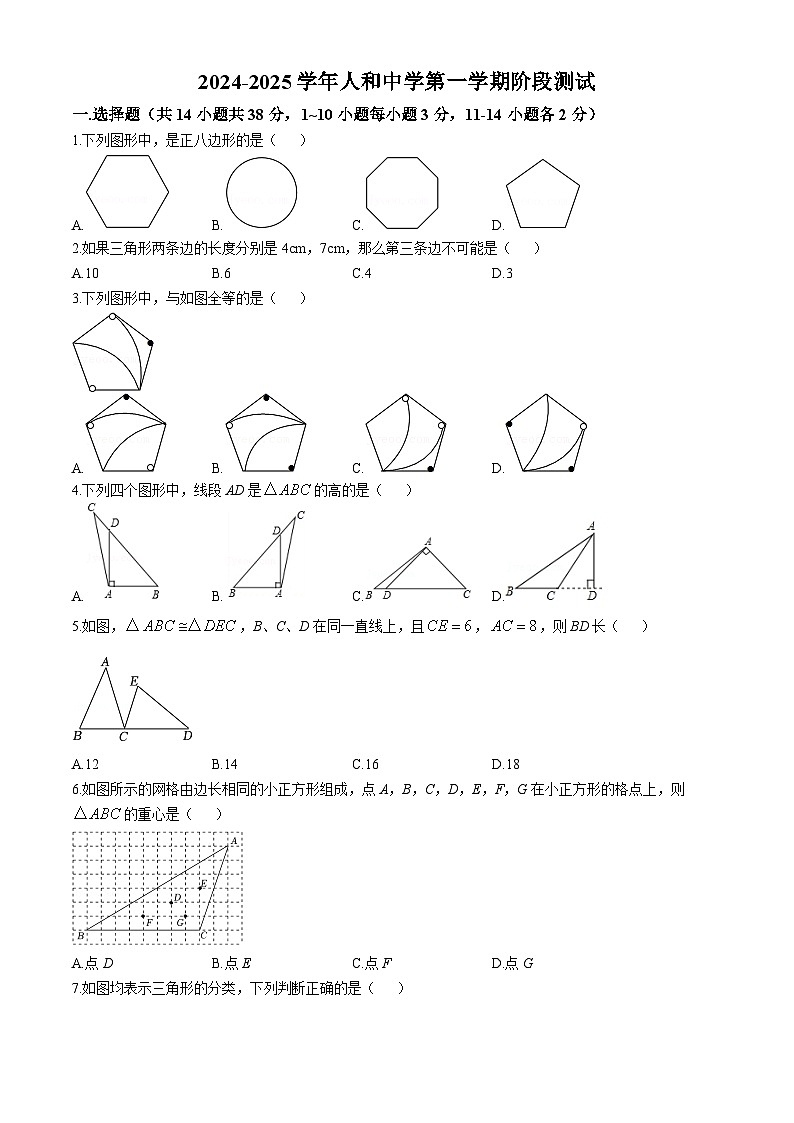
1.下列图形中，是正八边形的是（ ）
A.B.C.D.
2.如果三角形两条边的长度分别是4cm，7cm，那么第三条边不可能是（ ）
A.10B.6C.4D.3
3.下列图形中，与如图全等的是（ ）
A.B.C.D.
4.下列四个图形中，线段AD是的高的是（ ）
A.B.C.D.
5.如图，，B、C、D在同一直线上，且，，则BD长（ ）
A.12B.14C.16D.18
6.如图所示的网格由边长相同的小正方形组成，点A，B，C，D，E，F，G在小正方形的格点上，则的重心是（ ）
A.点DB.点EC.点FD.点G
7.如图均表示三角形的分类，下列判断正确的是（ ）
A.①对，②不对B.①不对，②对
C.①、②都不对D.①、②都对
8.如图，直角三角形被挡住了一部分，小明根据所学知识很快就另外画出了一个与原来完全一样的三角形，这两个三角形全等的依据是（ ）
A.SASB.ASAC.AASD.HL
9.如图，要想知道黑板上两直线a，b所夹锐角的大小，但因交点不在黑板内，无法直接测量，小慧设计了间接测量方案（相关标记和数据如图所示），则直线a，b所夹锐角的度数为（ ）
A.30°B.40°C.50°D.60°
10.如图，用四颗螺丝将不能弯曲的木条围成一个木框，不计螺丝大小，其中相邻两颗螺丝的距离依次为3、4、6、8，且相邻两根木条的夹角均可以调整，若调整木条的夹角时不破坏此木框，则任意两颗螺丝的距离的最大值是（ ）
A.7B.10C.11D.14
11.如图，已知∠AOB，以点O为圆心，以任意长为半径画弧①，分别交OA，OB于点E，F，再以点E为圆心，以EF长为半径画弧，交弧①于点D，画射线OD.若，则的度数为（ ）
A.32°B.54°C.64°D.68°
12.如图，小明从A地出发，沿直线前进15米后向左转18°，再沿直线前进15米，又向左转18°……，照这样走下去，他第一次回到出发地A地时，一共走的路程是（ ）
A.200米B.250米C.300米D.350米
13.已知，求作射线OC，使OC平分，那么作法的合理顺序是（ ）
①作射线OC；
②在射线OA和OB上分别截取OD、OE，使；
③分别以D、E为圆心，大于的长为半径在内作弧，两弧交于点C.
A.①②③B.②①③C.②③①D.③①②
14.为了解学生对所学知识的应用能力，某校老师在七年级数学兴趣小组活动中，设置了这样的问题：因为池塘两端A，B的距离无法直接测量，请同学们设计方案测量A，B的距离，甲、乙两位同学分别设计了如下两种方案：
甲：如图1，在平地上取一个可以直接到达点A，B的点O，连接AO并延长到点C，连接BO并延长到点D，使，，连接DC，测出DC的长即可.
乙：如图2，先确定直线AB，过点B作直线BE，在直线BE上找可以直接到达点A的一点D，连接DA，作，交直线AB于点C，最后测量BC的长即可.
其中可行的测量方案是（ ）
图1 图2
A.只有方案甲可行B.只有方案乙可行
C.方案甲和乙都可行D.方案甲和乙都不可行
二、填空题（共3小题，共10分，15小题2分，16~17小题各4分，每空2分）
15.如图，当自行车停车时，两个轮子和一个支撑脚着地，自行车就不会倒，其中蕴含的数学原理是______.
16.按照图中所示的方法将多边形分割成三角形，图（1）中三角形可分割出2个三角形；图（2）中四边形可分割出3个三角形；图（3）中五边形可分割出 ______个三角形；由此你能猜测出，n边形可以分害出______个三角形.
17.如图，BD平分的外角，，于点E，于点F.
（1）求证：______.
（2）若，，______.
三.解答题（共7小题，满分72分）
18.（9分）已知在中，，，且AC为奇数.
（1）求的周长；
（2）判断的形状.
19.（9分）在五边形中，五个角的度数表示如图，求x的值.
20.（9分）如图所示，为了固定电线杆AD，将两根长分别为10m的电线一端同系在电线杆A点上，另一端固定在地面上的两个锚上，那么两个锚离电线杆底部（D）的距离相等吗？为什么？
21.（10分）如图，中，于点D，BE平分，若，.
（1）求的度数；
（2）若点F为线段BC上的任意一点，当为直角三角形时，求的度数.
22.（10分）如图，课本上利用实验剪拼的方法，把和移动到的右侧，且使这三个角的顶点重合，再利用平行线的性质可以说明三角形内角和定理.
具体说理过程如下：
延长BC，过点C作.
∴______（两直线平行，内错角相等），
（______），
∵（平角定义），
∴（______）.
（1）请你补充完善上述说理过程；
（2）请你参考实验1的解题思路，自行画图标注好顶点字母，写出实验2说明三角形内角和定理的过程.
23.（12分）如图，在中，点D在BC边上，，的平分线交AC于点E，过点E作，垂足为F，且，连接DE.
（1）求的度数；
（2）求证：DE平分；
24.（13分）新定义：如果两个三角形不全等但面积相等，那么这两个三角形叫做积等三角形.
【初步尝试】
（1）如图1，在中，，，P为边BC上一点，若与是积等三角形，求BP的长；
【理解运用】
（2）如图2，与为积等三角形，若，，且线段AD的长度为正整数，求AD的长.
【综合应用】
（3）如图3，在中，，过点C作，点D是射线CM上一点，以AD为边作，，，连接BE.请判断与是否为积等三角形，并说明理由.
2024-2025学年人和中学第一学期阶段测试
参考答案
一.选择题（共14小题共38分，1~10小题每小题3分，11-14小题各2分）
1.C 2.D 3.A 4.D 5.B 6.A 7.B 8.B
9.B 10.B 11.C 12.C 13.C 14.A
二.填空题（共3小题，共10分，15小题2分，16~17小题各4分，每空2分）
15.三角形具有稳定性 16.4
17.（1） （2）1
三.解答题（共7小题，满分72分）
18.【解答】解：（1）由题意得：，
即：，
∵AC为奇数，
∴，
∴的周长为；
（2）∵，
∴是等腰三角形.
19.根据题意列方程得：，
解得.
20.【解答】解：两个锚离电线杆底部（D）的距离相等.理由如下：
依题意知，，则.
在与中，，
∴，
∴.
即两个锚离电线杆底部（D）的距离相等.
21.【解答】解：（1）∵BE平分，若，
∴，
∵，
∴，
∵于点D，
∴；
（2）∵，
∴当为直角三角形时，有以下两种情况：
①当时，如图1所示：
∵，，
∴，
∴；
图1
②当时，如图2所示：
∴，
∵，
∴.
综上所述：当为直角三角形时，的度数是20°或60°.
图2
22.（1） 两直线平行，同位角相等 等量代换
（2）证明：如图2所示，过点A作直线，∴，，
∵（平角定义），
∴.
23.【解答】（1）解：∵，，
∴，
∵，
∴；
（2）证明：过点E作于G，于H，
∵，，，
∴，
∵BE平分，，，
∴，
∴，
∵，，
∴DE平分；
24.【解答】解：（1）过点A作于H，如图1，
∵与是积等三角形，
∴，
∴，
∴，
∵，
∴；
图1
（2）如图2，延长AD至N，使，连接CN，
∵与为积等三角形，
∴，
在和中，，
∴，∴，
在中，，
∵，
∴，
∴，
∴，
∴，
∵AD为正整数，
∴；
图2
（3）积等三角形；
证明：如图3，过点E作于点H，
∵，
∴，
∵，
∴，
∴，
∴，
在和中，
，
∴，
∴，，
∵，，
∵AB=AC，
∴，∴，
∴与为积等三角形.
图3