浙江省台州市中考数学试卷（含解析版）

这是一份浙江省台州市中考数学试卷（含解析版），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

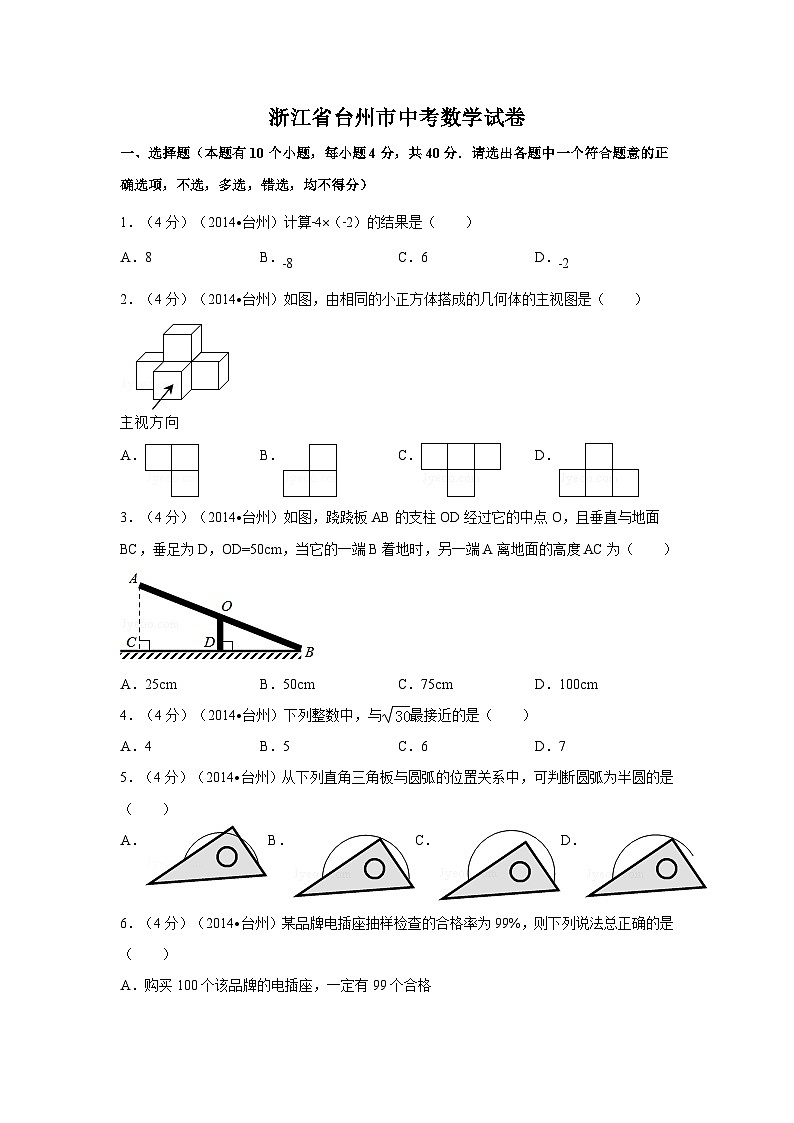
1．（4分）（2014•台州）计算﹣4×（﹣2）的结果是（ ）
2．（4分）（2014•台州）如图，由相同的小正方体搭成的几何体的主视图是（ ）
3．（4分）（2014•台州）如图，跷跷板AB的支柱OD经过它的中点O，且垂直与地面BC，垂足为D，OD=50cm，当它的一端B着地时，另一端A离地面的高度AC为（ ）
4．（4分）（2014•台州）下列整数中，与最接近的是（ ）
5．（4分）（2014•台州）从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是（ ）
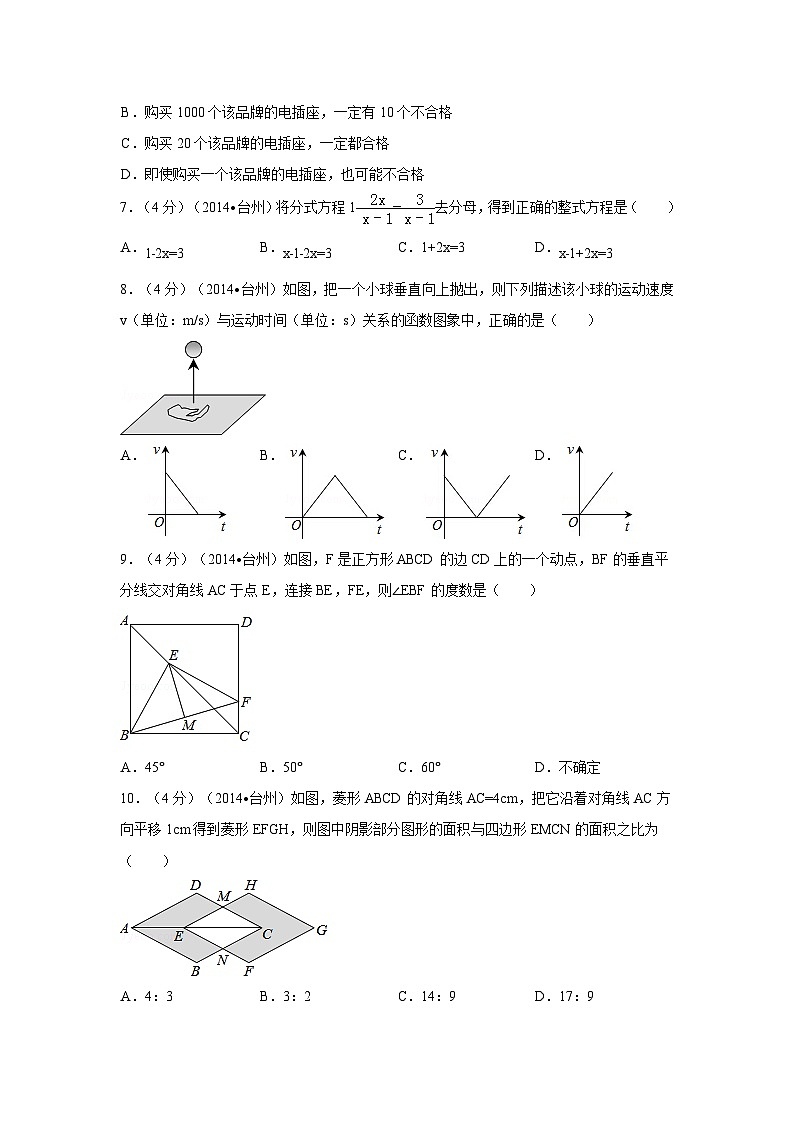
6．（4分）（2014•台州）某品牌电插座抽样检查的合格率为99%，则下列说法总正确的是（ ）
7．（4分）（2014•台州）将分式方程1﹣=去分母，得到正确的整式方程是（ ）
8．（4分）（2014•台州）如图，把一个小球垂直向上抛出，则下列描述该小球的运动速度v（单位：m/s）与运动时间（单位：s）关系的函数图象中，正确的是（ ）
9．（4分）（2014•台州）如图，F是正方形ABCD的边CD上的一个动点，BF的垂直平分线交对角线AC于点E，连接BE，FE，则∠EBF的度数是（ ）
10．（4分）（2014•台州）如图，菱形ABCD的对角线AC=4cm，把它沿着对角线AC方向平移1cm得到菱形EFGH，则图中阴影部分图形的面积与四边形EMCN的面积之比为（ ）

二、填空题（本题有6小题，每小题5分，共30分）
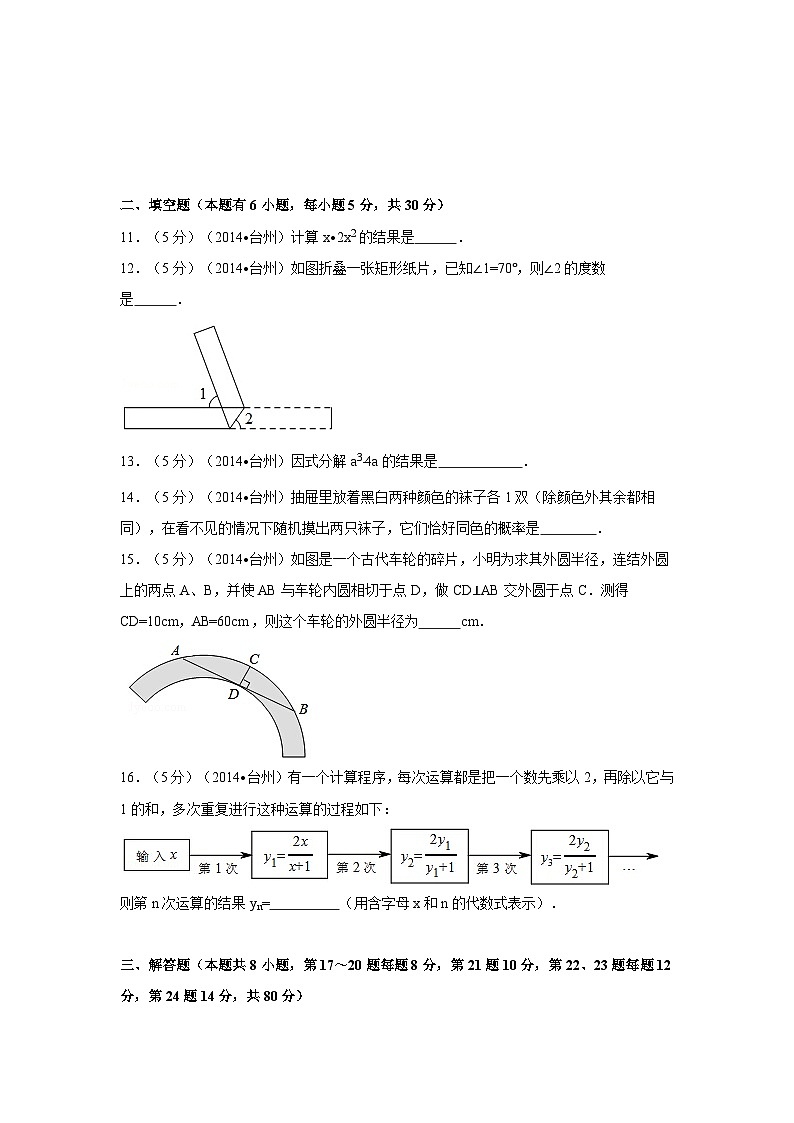
11．（5分）（2014•台州）计算x•2x2的结果是 ．
12．（5分）（2014•台州）如图折叠一张矩形纸片，已知∠1=70°，则∠2的度数是 ．
13．（5分）（2014•台州）因式分解a3﹣4a的结果是 ．
14．（5分）（2014•台州）抽屉里放着黑白两种颜色的袜子各1双（除颜色外其余都相同），在看不见的情况下随机摸出两只袜子，它们恰好同色的概率是 ．
15．（5分）（2014•台州）如图是一个古代车轮的碎片，小明为求其外圆半径，连结外圆上的两点A、B，并使AB与车轮内圆相切于点D，做CD⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径为 cm．

16．（5分）（2014•台州）有一个计算程序，每次运算都是把一个数先乘以2，再除以它与1的和，多次重复进行这种运算的过程如下：
则第n次运算的结果yn= （用含字母x和n的代数式表示）．

三、解答题（本题共8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17．（8分）（2014•台州）计算：|2﹣1|+（﹣1）0﹣（）﹣1．
18．（8分）（2014•台州）解不等式组：，并把解集在如图数轴上表示出来．
19．（8分）（2014•台州）已知反比函数y=，当x=2时，y=3．
（1）求m的值；
（2）当3≤x≤6时，求函数值y的取值范围．
20．（8分）（2014•台州）如图1是某公交汽车挡风玻璃的雨刮器，其工作原理如图2．雨刷EF⊥AD，垂足为A，AB=CD且AD=BC，这样能使雨刷EF在运动时，始终垂直于玻璃窗下沿BC，请证明这一结论．

21．（10分）（2014•台州）如图，某翼装飞行员从离水平地面高AC=500m的A处出发，沿这俯角为15°的方向，直线滑行1600米到达D点，然后打开降落伞以75°的俯角降落到地面上的B点．求他飞行的水平距离BC（结果精确到1m）．

22．（12分）（2014•台州）为了估计鱼塘中成品鱼（个体质量在0.5kg及以上，下同）的总质量，先从鱼塘中捕捞50条成品鱼，称得它们的质量如表：
然后做上记号再放回水库中，过几天又捕捞了100条成品鱼，发现其中2条带有记号．
（1）请根据表中数据补全如图的直方图（各组中数据包括左端点不包括右端点）．
（2）根据图中数据分组，估计从鱼塘中随机捕一条成品鱼，其质量落在哪一组的可能性最大？
（3）根据图中数据分组，估计鱼塘里质量中等的成品鱼，其质量落在哪一组内？
（4）请你用适当的方法估计鱼塘中成品鱼的总质量（精确到1kg）．

23．（12分）（2014•台州）某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类，A类杨梅包装后直接销售；B类杨梅深加工后再销售．A类杨梅的包装成本为1万元/吨，根据市场调查，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2）之间的函数关系如图；B类杨梅深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s=12+3t，平均销售价格为9万元/吨．
（1）直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式；
（2）第一次，该公司收购了20吨杨梅，其中A类杨梅有x吨，经营这批杨梅所获得的毛利润为w万元（毛利润=销售总收入﹣经营总成本）．
①求w关于x的函数关系式；
②若该公司获得了30万元毛利润，问：用于直销的A类杨梅有多少吨？
（3）第二次，该公司准备投入132万元，请设计一种经营方案，使公司获得最大毛利润，并求出最大毛利润．

24．（14分）（2014•台州）研究几何图形，我们往往先给出这类图形的定义，再研究它的性质和判定．
定义：六个内角相等的六边形叫等角六边形．
（1）研究性质
①如图1，等角六边形ABCDEF中，三组正对边AB与DE，BC与EF，CD与AF分别有什么位置关系？证明你的结论
②如图2，等角六边形ABCDEF中，如果有AB=DE，则其余两组正对边BC与EF，CD与AF相等吗？证明你的结论
③如图3，等角六边形ABCDEF中，如果三条正对角线AD，BE，CF相交于一点O，那么三组正对边AB与DE，BC与EF，CD与AF分别有什么数量关系？证明你的结论．
（2）探索判定
三组正对边分别平行的六边形，至少需要几个内角为120°，才能保证六边形一定是等角六边形？

A．
8
B．
﹣8
C．
6
D．
﹣2

A．
B．
C．
D．

A．
25cm
B．
50cm
C．
75cm
D．
100cm

A．
4
B．
5
C．
6
D．
7

A．
B．
C．
D．

A．
购买100个该品牌的电插座，一定有99个合格

B．
购买1000个该品牌的电插座，一定有10个不合格

C．
购买20个该品牌的电插座，一定都合格

D．
即使购买一个该品牌的电插座，也可能不合格

A．
1﹣2x=3
B．
x﹣1﹣2x=3
C．
1+2x=3
D．
x﹣1+2x=3

A．
B．
C．
D．

A．
45°
B．
50°
C．
60°
D．
不确定

A．
4：3
B．
3：2
C．
14：9
D．
17：9
质量/kg
0.5
0.6
0.7
1.0
1.2
1.6
1.9
数量/条
1
8
15
18
5
1
2
浙江省台州市中考数学试卷
参考答案与试题解析
一、选择题（本题有10个小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选，多选，错选，均不得分）
1．（4分）（2014•台州）计算﹣4×（﹣2）的结果是（ ）

2．（4分）（2014•台州）如图，由相同的小正方体搭成的几何体的主视图是（ ）

3．（4分）（2014•台州）如图，跷跷板AB的支柱OD经过它的中点O，且垂直与地面BC，垂足为D，OD=50cm，当它的一端B着地时，另一端A离地面的高度AC为（ ）

4．（4分）（2014•台州）下列整数中，与最接近的是（ ）

5．（4分）（2014•台州）从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是（ ）

6．（4分）（2014•台州）某品牌电插座抽样检查的合格率为99%，则下列说法总正确的是（ ）

7．（4分）（2014•台州）将分式方程1﹣=去分母，得到正确的整式方程是（ ）

8．（4分）（2014•台州）如图，把一个小球垂直向上抛出，则下列描述该小球的运动速度v（单位：m/s）与运动时间（单位：s）关系的函数图象中，正确的是（ ）

9．（4分）（2014•台州）如图，F是正方形ABCD的边CD上的一个动点，BF的垂直平分线交对角线AC于点E，连接BE，FE，则∠EBF的度数是（ ）

10．（4分）（2014•台州）如图，菱形ABCD的对角线AC=4cm，把它沿着对角线AC方向平移1cm得到菱形EFGH，则图中阴影部分图形的面积与四边形EMCN的面积之比为（ ）

二、填空题（本题有6小题，每小题5分，共30分）
11．（5分）（2014•台州）计算x•2x2的结果是 2x3 ．

12．（5分）（2014•台州）如图折叠一张矩形纸片，已知∠1=70°，则∠2的度数是 55° ．

13．（5分）（2014•台州）因式分解a3﹣4a的结果是 a（a+2）（a﹣2） ．

14．（5分）（2014•台州）抽屉里放着黑白两种颜色的袜子各1双（除颜色外其余都相同），在看不见的情况下随机摸出两只袜子，它们恰好同色的概率是 ．

15．（5分）（2014•台州）如图是一个古代车轮的碎片，小明为求其外圆半径，连结外圆上的两点A、B，并使AB与车轮内圆相切于点D，做CD⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径为 50 cm．


16．（5分）（2014•台州）有一个计算程序，每次运算都是把一个数先乘以2，再除以它与1的和，多次重复进行这种运算的过程如下：
则第n次运算的结果yn= （用含字母x和n的代数式表示）．

三、解答题（本题共8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17．（8分）（2014•台州）计算：|2﹣1|+（﹣1）0﹣（）﹣1．

18．（8分）（2014•台州）解不等式组：，并把解集在如图数轴上表示出来．

19．（8分）（2014•台州）已知反比函数y=，当x=2时，y=3．
（1）求m的值；
（2）当3≤x≤6时，求函数值y的取值范围．

20．（8分）（2014•台州）如图1是某公交汽车挡风玻璃的雨刮器，其工作原理如图2．雨刷EF⊥AD，垂足为A，AB=CD且AD=BC，这样能使雨刷EF在运动时，始终垂直于玻璃窗下沿BC，请证明这一结论．

21．（10分）（2014•台州）如图，某翼装飞行员从离水平地面高AC=500m的A处出发，沿这俯角为15°的方向，直线滑行1600米到达D点，然后打开降落伞以75°的俯角降落到地面上的B点．求他飞行的水平距离BC（结果精确到1m）．

22．（12分）（2014•台州）为了估计鱼塘中成品鱼（个体质量在0.5kg及以上，下同）的总质量，先从鱼塘中捕捞50条成品鱼，称得它们的质量如表：
然后做上记号再放回水库中，过几天又捕捞了100条成品鱼，发现其中2条带有记号．
（1）请根据表中数据补全如图的直方图（各组中数据包括左端点不包括右端点）．
（2）根据图中数据分组，估计从鱼塘中随机捕一条成品鱼，其质量落在哪一组的可能性最大？
（3）根据图中数据分组，估计鱼塘里质量中等的成品鱼，其质量落在哪一组内？
（4）请你用适当的方法估计鱼塘中成品鱼的总质量（精确到1kg）．

23．（12分）（2014•台州）某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类，A类杨梅包装后直接销售；B类杨梅深加工后再销售．A类杨梅的包装成本为1万元/吨，根据市场调查，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2）之间的函数关系如图；B类杨梅深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s=12+3t，平均销售价格为9万元/吨．
（1）直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式；
（2）第一次，该公司收购了20吨杨梅，其中A类杨梅有x吨，经营这批杨梅所获得的毛利润为w万元（毛利润=销售总收入﹣经营总成本）．
①求w关于x的函数关系式；
②若该公司获得了30万元毛利润，问：用于直销的A类杨梅有多少吨？
（3）第二次，该公司准备投入132万元，请设计一种经营方案，使公司获得最大毛利润，并求出最大毛利润．

24．（14分）（2014•台州）研究几何图形，我们往往先给出这类图形的定义，再研究它的性质和判定．
定义：六个内角相等的六边形叫等角六边形．
（1）研究性质
①如图1，等角六边形ABCDEF中，三组正对边AB与DE，BC与EF，CD与AF分别有什么位置关系？证明你的结论
②如图2，等角六边形ABCDEF中，如果有AB=DE，则其余两组正对边BC与EF，CD与AF相等吗？证明你的结论
③如图3，等角六边形ABCDEF中，如果三条正对角线AD，BE，CF相交于一点O，那么三组正对边AB与DE，BC与EF，CD与AF分别有什么数量关系？证明你的结论．
（2）探索判定
三组正对边分别平行的六边形，至少需要几个内角为120°，才能保证六边形一定是等角六边形？

A．
8
B．
﹣8
C．
6
D．
﹣2
考点：
有理数的乘法．
分析：
根据有理数的乘法运算法则进行计算即可得解．
解答：
解：﹣4×（﹣2），
=4×2，
=8．
故选A．
点评：
本题考查了有理数的乘法，是基础题，熟记运算法则是解题的关键．

A．
B．
C．
D．
考点：
简单组合体的三视图．
分析：
根据从正面看得到的图形是主视图，可得答案．
解答：
解；从正面看第一层是三个正方形，第二层是中间一个正方形，
故选：D．
点评：
本题考查了简单组合体的三视图，从正面看得到的图形是主视图．

A．
25cm
B．
50cm
C．
75cm
D．
100cm
考点：
三角形中位线定理
专题：
应用题．
分析：
判断出OD是△ABC的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半可得AC=2OD．
解答：
解：∵O是AB的中点，OD垂直于地面，AC垂直于地面，
∴OD是△ABC的中位线，
∴AC=2OD=2×50=100cm．
故选D．
点评：
本题考查了三角形的中位线平行于第三边并且等于第三边的一半，熟记定理是解题的关键．

A．
4
B．
5
C．
6
D．
7
考点：
估算无理数的大小
分析：
根据5，25 与30的距离小于36与30的距离，可得答案．
解答：
解：与最接近的是5，
故选：B．
点评：
本题考查了估算无理数的大小，两个被开方数的差小，算术平方根的差也小是解题关键．

A．
B．
C．
D．
考点：
圆周角定理．
分析：
根据圆周角定理（直径所对的圆周角是直角）求解，即可求得答案．
解答：
解：∵直径所对的圆周角等于直角，
∴从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是B．
故选B．
点评：
此题考查了圆周角定理．此题比较简单，注意掌握数形结合思想的应用．

A．
购买100个该品牌的电插座，一定有99个合格

B．
购买1000个该品牌的电插座，一定有10个不合格

C．
购买20个该品牌的电插座，一定都合格

D．
即使购买一个该品牌的电插座，也可能不合格
考点：
概率的意义．
分析：
根据概率的意义，可得答案．
解答：
解；A、B、C、说法都非常绝对，故A、B、C错误；
D、即使购买一个该品牌的电插座，也可能不合格，说法合理，故D正确；
故选：D．
点评：
本题考查了概率的意义，本题解决的关键是理解概率的意义以及必然事件的概念．

A．
1﹣2x=3
B．
x﹣1﹣2x=3
C．
1+2x=3
D．
x﹣1+2x=3
考点：
解分式方程．
专题：
计算题．
分析：
分式方程两边乘以最简公分母x﹣1，即可得到结果．
解答：
解：分式方程去分母得：x﹣1﹣2x=3，
故选B
点评：
此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．

A．
B．
C．
D．
考点：
动点问题的函数图象
分析：
一个小球垂直向上抛出，小球的运动速度v越来越小，到达最高点是为0，小球下落时速度逐渐增加，据此选择即可．
解答：
解：根据分析知，运动速度v先减小后增大，
故选：C．
点评：
本题主要考查了动点问题的函数图象．分析小球的运动过程是解题的关键．

A．
45°
B．
50°
C．
60°
D．
不确定
考点：
全等三角形的判定与性质；正方形的性质．
分析：
证明Rt△BHE≌Rt△EIF，可得∠IEF+∠HEB=90°，再根据BE=EF即可解题．
解答：
解：如图所示，过E作HI∥BC，分别交AB、CD于点H、I，则∠BHE=∠EIF=90°，
∵E是BF的垂直平分线EM上的点，
∴EF=EB，
∵E是∠BCD角平分线上一点，
∴E到BC和CD的距离相等，即BH=EI，
Rt△BHE和Rt△EIF中，
，
∴Rt△BHE≌Rt△EIF（HL），
∴∠HBE=∠IEF，
∵∠HBE+∠HEB=90°，
∴∠IEF+∠HEB=90°，
∴∠BEF=90°，
∵BE=EF，
∴∠EBF=∠EFB=45°，
故选A．
点评：
本题考查了正方形角平分线和对角线重合的性质，考查了直角三角形全等的判定，考查了全等三角形对应角相等的性质．

A．
4：3
B．
3：2
C．
14：9
D．
17：9
考点：
菱形的性质；平移的性质
分析：
首先得出△MEC∽△DAC，则=，进而得出=，即可得出答案．
解答：
解：∵ME∥AD，
∴△MEC∽△DAC，
∴=，
∵菱形ABCD的对角线AC=4cm，把它沿着对角线AC方向平移1cm得到菱形EFGH，
∴AE=1cm，EC=3cm，
∴=，
∴=，
∴图中阴影部分图形的面积与四边形EMCN的面积之比为：=．
故选：C．
点评：
此题主要考查了菱形的性质以及相似三角形的判定与性质，得出=是解题关键．
考点：
单项式乘单项式．
分析：
根据单项式与单项式相乘，把他们的系数分别相乘，相同字母的幂分别相加，其余字母连同他的指数不变，作为积的因式，计算即可．
解答：
解：x•2x2=2x3．
故答案是：2x3．
点评：
本题考查了单项式与单项式相乘，熟练掌握运算法则是解题的关键．
考点：
平行线的性质；翻折变换（折叠问题）．
分析：
根据折叠性质得出∠2=∠EFG，求出∠BEF，根据平行线性质求出∠CFE，即可求出答案．
解答：
解：
根据折叠得出∠EFG=∠2，
∵∠1=70°，
∴∠BEF=∠1=70°，
∵AB∥DC，
∴∠EFC=180°﹣∠BEF=110°，
∴∠2=∠EFG=∠EFC=55°，
故答案为：55°．
点评：
本题考查了平行线的性质，折叠的性质，对顶角相等的应用，解此题的关键是能根据平行线性质求出∠CFE的度数．!
考点：
提公因式法与公式法的综合运用
专题：
计算题．
分析：
原式提取a后，利用平方差公式分解即可．
解答：
解：原式=a（a2﹣4）
=a（a+2）（a﹣2）．
故答案为：a（a+2）（a﹣2）．
点评：
此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
考点：
列表法与树状图法
分析：
首先根据题意画出树状图，然后由树状图求得所有等可能的结果与它们恰好同色的情况，再利用概率公式即可求得答案．
解答：
解：画树状图得：
∵共有12种等可能的结果，它们恰好同色的有4种情况，
∴它们恰好同色的概率是：=．
故答案为：．
点评：
本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，用到的知识点为：概率=所求情况数与总情况数之比．
考点：
垂径定理的应用；勾股定理
分析：
设点O为外圆的圆心，连接OA和OC，根据CD=10cm，AB=60cm，设设半径为r，则OD=r﹣10，根据垂径定理得：r2=（r﹣10）2+302，求得r的值即可．
解答：
解：如图，设点O为外圆的圆心，连接OA和OC，
∵CD=10cm，AB=60cm，
∴设半径为r，则OD=r﹣10，
根据题意得：r2=（r﹣10）2+302，
解得：r=50，
故答案为50．
点评：
本题考查了垂径定理的应用，解题的关键是正确构造直角三角形．
考点：
分式的混合运算．
专题：
图表型；规律型．
分析：
将y1代入y2计算表示出y2，将y2代入y3计算表示出y3，归纳总结得到一般性规律即可得到结果．
解答：
解：将y1=代入得：y2==；
将y2=代入得：y3==，
依此类推，第n次运算的结果yn=．
故答案为：
点评：
此题考查了分式的混合运算，找出题中的规律是解本题的关键．
考点：
实数的运算；零指数幂；负整数指数幂．
分析：
分别根据0指数幂及负整数指数幂的运算法则、绝对值的性质计算出各数，再根据实数混合运算的法则进行计算即可；
解答：
解：原式=2﹣1+1﹣
=．
点评：
本题考查的是实数的运算，熟知0指数幂及负整数指数幂的运算法则、绝对值的性质是解答此题的关键．
考点：
解一元一次不等式组；在数轴上表示不等式的解集．
分析：
先求出每个不等式的解集，再求出不等式组的解集，最后在数轴上表示出来即可．
解答：
解：
∵解不等式①得：x＞2，
解不等式②得：x＜3，
∴不等式组的解集为2＜x＜3，
在数轴上表示为：
．
点评：
本题考查了解一元一次不等式和解一元一次不等式组，在数轴上表示不等式组的解集的应用，解此题的关键是求出不等式组的解集．
考点：
待定系数法求反比例函数解析式；反比例函数的性质
分析：
（1）把x、y的值代入反比例函数解析式，通过方程来求m的值；
（2）根据反比例函数图象的性质进行解答．
解答：
解：（1）把x=2时，y=3代入y=，得
3=，
解得：m=﹣1；
（2）由m=﹣1知，该反比例函数的解析式为：y=．
当x=3时，y=2；
当x=6时，y=1．
∴当3≤x≤6时，函数值y的取值范围是：1≤y≤2．
点评：
本题考查了反比例函数的性质，待定系数法求反比例函数解析式．（1）题，实际上是把已知条件（自变量与函数的对应值）代入解析式，得到待定系数的方程
考点：
平行四边形的判定与性质．
专题：
应用题．
分析：
首先证明四边形ABCD是平行四边形，然后根据平行四边形的性质即可判断．
解答：
证明：∵AB=CD、AD=BC，
∴四边形ABCD是平行四边形，
∴AD∥BC，
又∵EF⊥AD，
∴EF⊥BC．
点评：
本题考查了平行四边形的判定与性质，正确理解平行四边形的判定方法是关键．
考点：
解直角三角形的应用-仰角俯角问题．
分析：
首先过点D作DE⊥AC于点E，过点D作DF⊥BC于点F，进而里锐角三角函数关系得出DE、AE的长，即可得出DF的长，求出BC即可．
解答：
解：过点D作DE⊥AC于点E，过点D作DF⊥BC于点F，
由题意可得：∠ADE=15°，∠BDF=15°，AD=1600m，AC=500m，
∴cs∠ADE=cs15°=≈0.97，
∴≈0.97，
解得：DE=1552（m），
sin15°=≈0.26，
∴≈0.26，
解得；AE=416（m），
∴DF=500﹣416=84（m），
∴tan∠BDF=tan15°=≈0.27，
∴≈0.27，
解得：BF=22.68（m），
∴BC=CF+BF=1552+22.68=1574.68≈1575（m），
答：他飞行的水平距离为1575m．
点评：
此题主要考查了解直角三角形的应用，正确构造直角三角形得出CF，BF的长是解题关键．
质量/kg
0.5
0.6
0.7
1.0
1.2
1.6
1.9
数量/条
1
8
15
18
5
1
2
考点：
频数（率）分布直方图；用样本估计总体．
分析：
（1）由函数图象可以得出1.1﹣1.4的有5条，就可以补全直方图；
（2）分别求出各组的频率，就可以得出结论；
（3）由这组数据的个数为50，就可以得出第25个和第26个数的平均数就可以得出结论；
（4）设鱼塘中成品鱼的总质量为x，根据作记号的鱼50：x=2：100建立方程求出其解即可．
解答：
解：（1）由函数图象可以得出1.1﹣1.4的有5条，补全图形，得：
（2）由题意，得
0.5﹣0.8的频率为：24÷50=0.48，
0.8﹣1.1的频率为：18÷50=0.36，
1.1﹣1.4的频率为：5÷50=0.1，
1.4﹣1.7的频率为：1÷50=0.02，
1.7﹣2.0的频率为：2÷50=0.04．
∵0.48＞0.36＞0.1＞0.04＞0.02．
∴估计从鱼塘中随机捕一条成品鱼，其质量落在0.5﹣0.8的可能性最大；
（3）这组数据的个数为50，就可以得出第25个和第26个数分别是1.0，1.0，
∴（1.0+1.0）÷2=1.0
鱼塘里质量中等的成品鱼，其质量落在0.8﹣1.1内；
（4）设鱼塘中成品鱼的总质量为x，由题意，得
50：x=2：100，
解得：x=2500．
2500×=2260kg．
点评：
本题考查了频数分布直方图的运用，比较频率大小的运用，中位数的运用，平均数的运用，由样本数据估计总体数据的运用，解答时认真分析统计表和统计图的数据是关键．
考点：
二次函数的应用
分析：
（1）这是一个分段函数，分别求出其函数关系式；
（2）①当2≤x＜8时及当x≥8时，分别求出w关于x的表达式．注意w=销售总收入﹣经营总成本=wA+wB﹣3×20；
②若该公司获得了30万元毛利润，将30万元代入①中求得的表达式，求出A类杨梅的数量；
（3）本问是方案设计问题，总投入为132万元，这笔132万元包括购买杨梅的费用+A类杨梅加工成本+B类杨梅加工成本．共购买了m吨杨梅，其中A类杨梅为x吨，B类杨梅为（m﹣x）吨，分别求出当2≤x＜8时及当x≥8时w关于x的表达式，并分别求出其最大值．
解答：
解：（1）①当2≤x＜8时，如图，
设直线AB解析式为：y=kx+b，将A（2，12）、B（8，6）代入得：
，解得，
∴y=﹣x+14；
②当x≥8时，y=6．
∴A类杨梅平均销售价格y与销售量x之间的函数关系式为：
y=．
（2）设销售A类杨梅x吨，则销售B类杨梅（20﹣x）吨．
①当2≤x＜8时，
wA=x（﹣x+14）﹣x=﹣x2+13x；
wB=9（20﹣x）﹣[12+3（20﹣x）]=108﹣6x
∴w=wA+wB﹣3×20
=（﹣x2+13x）+（108﹣6x）﹣60
=﹣x2+7x+48；
当x≥8时，
wA=6x﹣x=5x；
wB=9（20﹣x）﹣[12+3（20﹣x）]=108﹣6x
∴w=wA+wB﹣3×20
=（5x）+（108﹣6x）﹣60
=﹣x+48．
∴w关于x的函数关系式为：
w=．
②当2≤x＜8时，﹣x2+7x+48=30，解得x1=9，x2=﹣2，均不合题意；
当x≥8时，﹣x+48=30，解得x=18．
∴当毛利润达到30万元时，直接销售的A类杨梅有18吨．
（3）设该公司用132万元共购买了m吨杨梅，其中A类杨梅为x吨，B类杨梅为（m﹣x）吨，
则购买费用为3m万元，A类杨梅加工成本为x万元，B类杨梅加工成本为[12+3（m﹣x）]万元，
∴3m+x+[12+3（m﹣x）]=132，化简得：x=3m﹣60．
①当2≤x＜8时，
wA=x（﹣x+14）﹣x=﹣x2+13x；
wB=9（m﹣x）﹣[12+3（m﹣x）]=6m﹣6x﹣12
∴w=wA+wB﹣3×m
=（﹣x2+13x）+（6m﹣6x﹣12）﹣3m
=﹣x2+7x+3m﹣12．
将3m=x+60代入得：w=﹣x2+8x+48=﹣（x﹣4）2+64
∴当x=4时，有最大毛利润64万元，
此时m=，m﹣x=；
②当x＞8时，
wA=6x﹣x=5x；
wB=9（m﹣x）﹣[12+3（m﹣x）]=6m﹣6x﹣12
∴w=wA+wB﹣3×m
=（5x）+（6m﹣6x﹣12）﹣3m
=﹣x+3m﹣12．
将3m=x+60代入得：w=48
∴当x＞8时，有最大毛利润48万元．
综上所述，购买杨梅共吨，其中A类杨梅4吨，B类吨，公司能够获得最大毛利润，最大毛利润为64万元．
点评：
本问是二次函数、一次函数的综合应用题，难度较大．解题关键是理清售价、成本、利润三者之间的关系．涉及到分段函数时，注意要分类讨论．
考点：
四边形综合题；全等三角形的判定与性质；多边形内角与外角；平行四边形的判定与性质；相似三角形的判定与性质
专题：
证明题；新定义；探究型．
分析：
（1）通过验证容易得到猜想：三组正对边分别平行．要证明两条线段平行，只需证明同位角相等或内错角相等或同旁内角互补，要证AB∥DE，只需连接AD，证明∠ADE=∠DAB即可，其它两组同理可得．
（2）要证BC=EF，CD=AF，只需连接AE、BD，证明△AFE≌△DCB即可．
（3）由条件“三条正对角线AD，BE，CF相交于一点O“及（1）中的结论可证到=，将等角六边形ABCDEF补成等边三角形后，可以证到AB+AF=DE+DC，从而得到三组正对边分别相等．
（4）若只有1个内角为120°或有2个内角为120°，可以通过举反例说明该六边形不一定是等角六边形；若有3个内角为120°，可以通过分类讨论证明该六边形一定是等角六边形．
解答：
解：（1）①结论：AB∥DE，BC∥EF，CD∥AF．
证明：连接AD，如图1，
∵六边形ABCDEF是等角六边形，∴∠BAF=∠F=∠E=∠EDC=∠C=∠B==120°．
∵∠DAF+∠F+∠E+∠EDA=360°，∴∠DAF+∠EDA=360°﹣120°﹣120°=120°．
∵∠DAF+∠DAB=120°，∴∠DAB=∠EDA．∴AB∥DE．
同理BC∥EF，CD∥AF．
②结论：EF=BC，AF=DC．
证明：连接AE、DB，如图2，
∵AB∥DE，AB=DE，∴四边形ABDE是平行四边形．
∴AE=DB，∠EAB=∠BDE．
∵∠BAF=∠EDC．∴∠FAE=∠CDB．
在△AFE和△DCB中，
．
∴△AFE≌△DCB．
∴EF=BC，AF=DC．
③结论：AB=DE，AF=DC，EF=BC．
延长FE、CD相交于点P，延长EF、BA相交于点Q，延长DC、AB相交于点S，如图3．
∵六边形ABCDEF是等角六边形，∴∠BAF=∠AFE=120°．∴∠QAF=∠QFA=60°．
∴△QAF是等边三角形．∴∠Q=60°，QA=QF=AF．
同理：∠S=60°，SB=SC=BC；∠P=60°，PE=PD=ED．
∵∠S=∠P=60°，∴△PSQ是等边三角形．∴PQ=QS=SP．
∴QB=QS﹣BS=PS﹣CS=PC．∴AB+AF=AB+QA=QB=PC=PD+DC=ED+DC．
∵AB∥ED，∴△AOB～△DOE．∴．
同理：，．
∴．
∴==1．
∴AB=ED，AF=DC，EF=BC．
（2）连接BF，如图4，
∵BC∥EF，∴∠CBF+∠EFB=180°．
∵∠A+∠ABF+∠AFB=180°，∴∠ABC+∠A+∠AFE=360°．
同理：∠A+∠ABC+∠C=360°．
∴∠AFE=∠C．
同理：∠A=∠D，∠ABC=∠E．
Ⅰ．若只有1个内角等于120°，不能保证该六边形一定是等角六边形．
反例：当∠A=120°，∠ABC=150°时，∠D=∠A∠=120°，∠E=∠ABC=150°．
∵六边形的内角和为720°，∴∠AFE=∠C=（720°﹣120°﹣120°﹣150°﹣150°）=90°．
此时该六边形不是等角六边形．
Ⅱ．若有2个内角等于120°，也不能保证该六边形一定是等角六边形．
反例：当∠A=∠D=120°，∠ABC=150°时，∠E=∠ABC=150°．
∵六边形的内角和为720°，∴∠AFE=∠C=（720°﹣120°﹣120°﹣150°﹣150°）=90°．
此时该六边形不是等角六边形．
Ⅲ．若有3个内角等于120°，能保证该六边形一定是等角六边形．
设∠A=∠D=α，∠ABC=∠E=β，∠AFE=∠C=γ．则2α+2β+2γ=720°．∴α+β+γ=360°．
∵有3个内角等于120°，∴α、β、γ中至少有两个为120°．
若α、β、γ都等于120°，则六个内角都等于120°；
若α、β、γ中有两个为120°，根据α+β+γ=360°可得第三个也等于120°，则六个内角都等于120°．
综上所述：至少有3个内角等于120°，能保证该六边形一定是等角六边形．
点评：
本题引导学生对几何图形进行科学探究（从定义到性质到判定），考查了相似三角形、全等三角形以及平行四边形的性质与判定、多边形的内角和定理等知识，考查了分类讨论的思想，培养了学生的批判意识（举反例说明一个命题是假命题），是一道非常难得的好题．