2024年贵州铜仁伟才学校九年级数学第一学期开学监测模拟试题【含答案】

这是一份2024年贵州铜仁伟才学校九年级数学第一学期开学监测模拟试题【含答案】，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）从下面四个条件中任意选两个，能使四边形ABCD是平行四边形选法有（ ）
①；②；③；④
A．2种B．3种C．4种D．5种
2、（4分）因式分解的正确结果是（ ）
A．B．C．D．
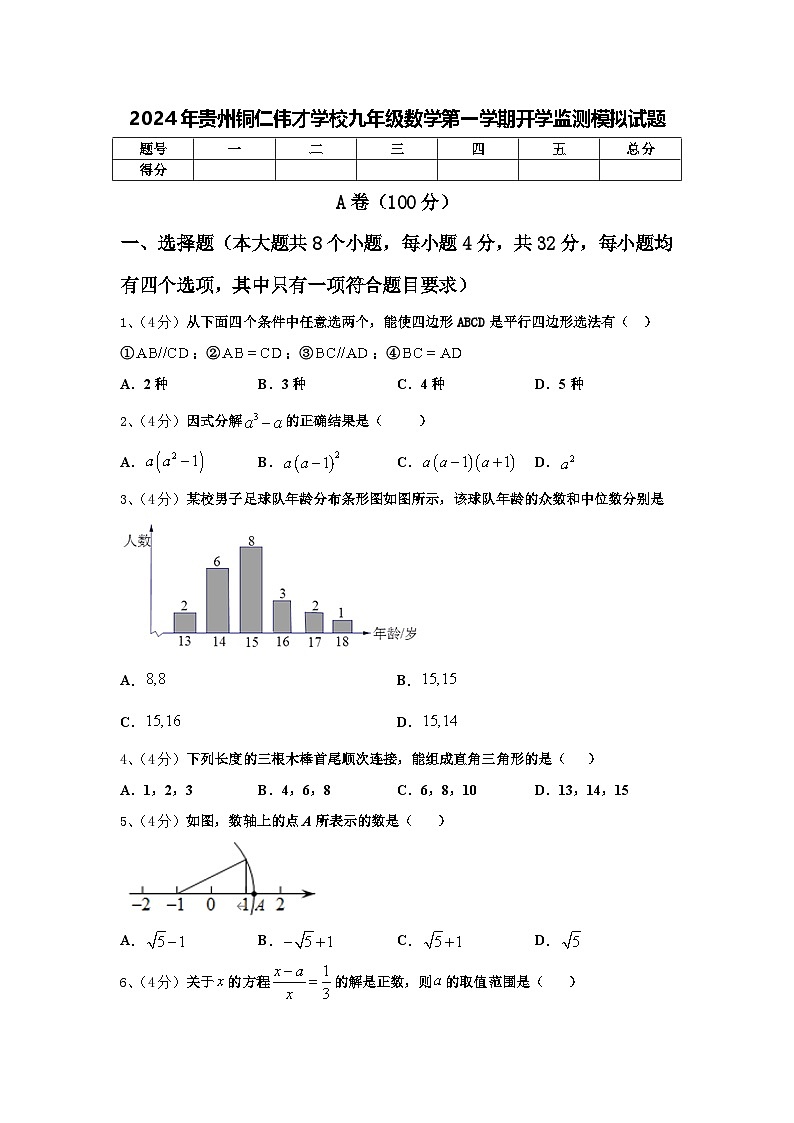
3、（4分）某校男子足球队年龄分布条形图如图所示，该球队年龄的众数和中位数分别是
A．B．
C．D．
4、（4分）下列长度的三根木棒首尾顺次连接，能组成直角三角形的是（ ）
A．1，2，3B．4，6，8C．6，8，10D．13，14，15
5、（4分）如图，数轴上的点A所表示的数是（ ）
A．B．C．D．
6、（4分）关于的方程的解是正数，则的取值范围是（ ）
A．B．C．D．
7、（4分）如图，在▱ABCD中，AB=3，BC=5，AC的垂直平分线交AD于E，则△CDE的周长是（ ）
A．8B．6C．9D．10
8、（4分）某个函数自变量的取值范围是x≥-1，则这个函数的表达式为（ ）
A．y=x+1B．y=x2+1C．y=D．y=
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在矩形中，对角线，交于点，要使矩形成为正方形，应添加的一个条件是______.
10、（4分）某单位向一所希望小学赠送1080件文具，现用A、B两种不同的包装箱进行包装，已知每个B型包装箱比A型包装箱多装15件文具，单独使用B型包装箱比单独使用A型包装箱可少用12个.设A型包装箱每个可以装件文具，根据题意列方程为 .
11、（4分）化简的结果是______．
12、（4分）若一个正多边形的每一个外角都是30°，则这个正多边形的内角和等于__________度．
13、（4分）在平面直角坐标系中，正比例函数与反比例函数的图象交于点，则_________.
三、解答题（本大题共5个小题，共48分）
14、（12分）今年，我区某中学响应“足球进校园”的号召，开设了“足球大课间”活动．现需要购进100个某品牌的足球供学生使用．经调查，该品牌足球2017年单价为200元，2019年单价为162元．
（1）求2017年到2019年该品牌足球单价平均每年降低的百分率；
（2）选购期间发现该品牌足球在标价162元的基础上，两个文体用品商店有下列不同的促销方案，试问去哪个商店买足球更优惠？
15、（8分）如图，在正方形ABCD中，P是CD边上一点，DF⊥AP，BE⊥AP．
求证：AE=DF．
16、（8分）如图，在矩形ABCD中，AB=4，AD=10，点E在AD边上，已知B、E两点关于直线l对称，直线l分别交AD、BC边于点M、N，连接BM、NE．
（1）求证：四边形BMEN是菱形；
（2）若DE=2，求NC的长．
17、（10分）我县“果菜大王”王大炮收货番茄20吨，青椒12吨．现计划租用甲、乙两种货车共8辆将这批果菜全部运往外地销售，已知一辆甲种货车可装番茄4吨和青椒1吨，一辆乙种货车可装番茄和青椒各2吨．
（1）王灿有几种方案安排甲、乙两种货车可一次性地将果菜运到销售地？
（2）若甲种货车每辆要付运输费300元，乙种货车每辆要付运输费240元，则果农王大炮应选择哪种方案，使运输费最少？最少运费是多少？
18、（10分）如图，正方形ABCD的边长为，点P为对角线BD上一动点，点E在射线BC上，
(1)填空：BD=______；
(2)若BE=t，连结PE、PC，求PE+PC的最小值(用含t的代数式表示);
(3)若点E是直线AP与射线BC的交点，当△PCE为等腰三角形时，求∠PEC的度数．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去.则第2016个正方形的边长为_____
20、（4分）如图，在平面直角坐标系中，点A（0，4），B（3，0），连接AB，将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为 ．
21、（4分）已知中，，角平分线BE、CF交于点O，则 ______ ．
22、（4分）已知正方形的边长为1，如果将向量的运算结果记为向量，那么向量的长度为______
23、（4分）命题“对角线相等的四边形是矩形”的逆命题是_____________．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图①，已知正方形ABCD的边长为1，点P是AD边上的一个动点，点A关于直线BP的对称点是点Q，连接PQ、DQ、CQ、BQ，设AP＝x．
（1）BQ＋DQ的最小值是_______，此时x的值是_______；
（2）如图②，若PQ的延长线交CD边于点E，并且∠CQD＝90°．
①求证：点E是CD的中点； ②求x的值．
（3）若点P是射线AD上的一个动点，请直接写出当△CDQ为等腰三角形时x的值．
25、（10分）如图，直线与直线相交于点．
（1）求，的值；
（2）根据图像直接写出时的取值范围；
（3）垂直于轴的直线与直线，分别交于点，，若线段长为2，求的值．
26、（12分）如图，在四边形ABCD中，BD为一条对角线，且，，E为AD的中点，连接BE．
（1）求证：四边形BCDE为菱形；
（2）连接AC，若AC平分，，求AC的长．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据平行四边形的五种判定方法，灵活运用平行四边形的判定定理，可作出判断．
【详解】
解：①和③根据两组对边分别平行的四边形是平行四边形，能推出四边形ABCD为平行四边形；
①和②，③和④根据一组对边平行且相等的四边形是平行四边形，能推出四边形ABCD为平行四边形；
②和④根据两组对边分别相等的四边形是平行四边形，能推出四边形ABCD为平行四边形；
所以能推出四边形ABCD为平行四边形的有四组
故选C．
本题考查了平行四边形的判定，熟练掌握判定定理是解题的关键．平行四边形共有五种判定方法，记忆时要注意技巧；这五种方法中，一种与对角线有关，一种与对角有关，其他三种与边有关．
2、C
【解析】
首先提取公因式a，再利用平方差公式进行二次分解即可．
【详解】
=a（a-1）=，
故选：C．
此题考查提公因式法与公式法的综合运用，解题关键在于掌握运算法则.
3、B
【解析】
根据条形图，观察可得15岁的人数最多，因此可得众数是15，将岁数从大到小排列，根据最中间的那个数就是中位数.
【详解】
首先根据条形图可得15岁的人数最多，
因此可得众数是15;
将岁数从大到小排列，根据条形图可知有人数：，
因此可得最中间的11和12个的平均值是中位数，11和12个人都是15岁，
故可得中位数是15.
本题主要考查众数和中位数的计算，是数据统计的基本知识，应当熟练掌握.
4、C
【解析】
判断是否为直角三角形，只要验证两小边的平方和等于最长边的平方即可．
【详解】
A、12+22=5≠32，故不能组成直角三角形，错误；
B、42+62≠82，故不能组成直角三角形，错误；
C、62+82=102，故能组成直角三角形，正确；
D、132+142≠152，故不能组成直角三角形，错误．
故选：C．
考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
5、A
【解析】
由题意，利用勾股定理求出点A到−1的距离，即可确定出点A表示的数．
【详解】
根据题意得：数轴上的点A所表示的数为−1＝，
故选：A．
此题考查了实数与数轴，弄清点A表示的数的意义是解本题的关键．
6、D
【解析】
先求得分式方程的解，再由题意可得关于x的不等式，解不等式即得答案.
【详解】
解：解方程，得，
因为方程的解是正数，所以，
所以，解得.
故选D.
本题考查了分式方程的解法和不等式的解法，熟练掌握分式方程和不等式的解法是解题的关键.
7、A
【解析】
由AC的垂直平分线交AD于E，易证得AE=CE，又由四边形ABCD是平行四边形，即可求得AD与DC的长，继而求得答案
【详解】
∵AC的垂直平分线交AD于E，
∴AE=CE，
∵四边形ABCD是平行四边形，
∴CD=AB=3，AD=BC=5，
∴△CDE的周长是：DC+DE+CE=DC+DE+AE=DC+AD=3+5=8，
故选A.
此题考查线段垂直平分线的性质，平行四边形的性质，解题关键在于得到AE=CE
8、C
【解析】
根据被开方数大于等于0，分母不等于0分别求出各选项的函数的取值范围，从而得解．
【详解】
解：A、自变量的取值范围是全体实数，故本选项错误；
B、自变量的取值范围是全体实数，故本选项错误；
C、由x+1≥0得，x≥-1，故本选项正确；
D、由x+10得，x-1，故本选项错误．
故选：C．
本题考查了函数自变量的范围，一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（答案不唯一）
【解析】
根据正方形的判定添加条件即可．
【详解】
解：添加的条件可以是AB＝BC．
理由如下：
∵四边形ABCD是矩形，AB＝BC，
∴四边形ABCD是正方形．
故答案为：AB＝BC（答案不唯一）．
本题考查了矩形的性质，正方形的判定的应用，能熟记正方形的判定定理是解此题的关键，注意：有一组邻边相等的矩形是正方形，对角线互相垂直的矩形是正方形．此题是一道开放型的题目，答案不唯一，也可以添加AC⊥BD．
10、
【解析】
单独使用B型包装箱比单独使用A型包装箱可少用12个；可列等量关系为：所用B型包装箱的数量+12=所用A型包装箱的数量，由此可得到所求的方程
【详解】
解：根据题意，得：
11、
【解析】
根据分式的减法和乘法可以解答本题．
【详解】
解:
,
故答案为:
本题考查分式的混合运算，解答本题的关键是明确分式混合运算的计算方法．
12、1800
【解析】
多边形的外角和等于360°，则正多边形的边数是360°÷30°=12，所以正多边形的内角和为.
13、
【解析】
把代入可得：解得得，再把代入，即，解得.
【详解】
解：把代入可得：
解得，
∴
∵点也在图象上，
把代入，
即，
解得.
故答案为：8
本题考查了一次函数和反比例函数，掌握待定系数法求解析式是关键.
三、解答题（本大题共5个小题，共48分）
14、（1）2017 年到 2019 年该品牌足球单价平均每年降低10%；（2）去B商店买足球更优惠，见解析
【解析】
（1）设平均每年降低的百分率为x，根据2017年及2019年该品牌足球的单价，即可得出关于x的一元二次方程，解之取其小于1的值即可得出结论；
（2）根据两商城的促销方案，分别求出在两商城购买100个该品牌足球的总费用，比较后即可得出结论．
【详解】
（1）设平均每年降低的百分率为，根据题意列方程，得．
解得：，（不合题意，舍去）．
答：2017 年到 2019 年该品牌足球单价平均每年降低10%；
（2）A商店：162×91=14742（元）；
B商店：162×0.9×100=1（元）．
因为14742＞1．
所以，去B商店买足球更优惠．
本题考查了一元二次方程的应用，解题的关键是：（1）根据2017年及2019年该品牌足球的单价，列出关于x的一元二次方程；（2）根据两商城的促销方案，分别求出在两商城购买100个该品牌足球的总费用．
15、详见解析
【解析】
根据正方形的性质可得AB=AD，∠BAD=90°，再根据∠AEB=∠AFD=90°，∠ABE+∠BAE=90°，得到∠ABE=∠DAF，然后通过“角角边”证得△ABE ≌△ADF，则可得AE=DF．
【详解】
证明∵四边形ABCD为正方形，
∴AB=AD，∠BAD=90°，
∴∠DAF+∠BAE=90°，
又∵DF⊥AP，BE⊥AP，
∴∠AEB=∠AFD=90°，
∴∠ABE+∠BAE=90°，
∴∠ABE=∠DAF，
在△ABE 与△ADF中，
，
∴△ABE ≌△ADF（AAS），
∴AE=DF（全等三角形对应边相等）.
16、（1）证明见解析； (2)NC=1.
【解析】
（1）根据B、E两点关于直线l对称，可得BM=ME，BN=NE，再根据矩形的性质可得BM=BN，从而得出BM=ME=BN=NE，通过四边相等的四边形是菱形即可得出结论;(2) 菱形边长为x，利用勾股定理计算即可.
【详解】
（1）∵ B、E两点关于直线l对称
∴ BM=ME，BN=NE，∠BMN=∠EMN在矩形ABCD中，AD∥BC
∴ ∠EMN=∠MNB
∴ ∠BMN=∠MNB
∴ BM=BN
∴ BM=ME=BN=NE
∴ 四边形ECBF是菱形．
(2)设菱形边长为x
则 AM=8-x
在Rt△ABM中，
∴ x=1．
∴NC=1.
本题考查了轴对称的性质及勾股定理的应用，解题的关键是熟记轴对称的性质.
17、（1）三种方案；（2）最少运费是2010元．
【解析】
试题分析：（1）设安排甲种货车x辆，则安排乙种货车（8-x）辆，根据车辆运送的番茄要求大于或等于20吨，青椒大于或等于12吨，可得出不等式组，解出即可．
（2）分别计算每种方案的运费，然后比较即可得出答案．
试题解析：（1）设安排甲种货车x辆，则安排乙种货车（8-x）辆，
依题意得：，
解得：2≤x≤1，
∵x是正整数，
∴x可取的值为2，3，1．
因此安排甲、乙两种货车有如下三种方案：
（2）方案一所需运费为300×2+210×6=2 010元；
方案二所需运费为300×3+210×5=2 100元；
方案三所需运费为300×1+210×1=2 160元．
答：王大炮应选择方案一运费最少，最少运费是2010元．
18、（1）BD=2 （2） （3）120° 30°
【解析】
.
分析：（1）根据勾股定理计算即可；
（2）连接AP，当AP与PE在一条线上时，PE+PC最小，利用勾股定理求出最小值；
（3）分两种情况考虑：①当E在BC延长线上时，如图2所示，△PCE为等腰三角形，则CP=CE；②当E在BC上，如图3所示，△PCE是等腰三角形，则PE=CE，分别求出∠PEC的度数即可．
详解：（1）BD==2 ；
（2）如图1所示：当AP与PE在一条线上时，PE+PC最小，

∵AB=，BE=t，
∴PE+PC的最小值为，
（3）分两种情况考虑：
①当点E在BC的延长线上时，

如图2所示，△PCE是等腰三角形，则CP=CE，
∴∠CPE=∠CEP，
∴∠BCP=∠CPE+∠CEP=2∠CEP，
∵在正方形ABCD中，∠ABC=90°，
∴∠PBA=∠PBC=45°，
在△ABP和△CBP中，
，
∴△ABP≌△CBP（SAS），
∴∠BAP=∠BCP=2∠CEP，
∵∠BAP+∠PEC=90°，
∴2∠PEC+∠PEC=90°，
∴∠PEC=30°；
②当点E在BC上时，

如图3所示，△PCE是等腰三角形，则PE=CE，
∴∠CPE=∠PCE，
∴∠BEP=∠CPE+∠PCE=2∠ECP，
∵四边形ABCD是正方形，
∴∠PBA=∠PBC=45°，
又AB=BC，BP=BP，
∴△ABP≌△CBP，
∴∠BAP=∠BCP，
∵∠BAP+∠AEB=90°，
∴2∠BCP+∠BCP=90°，
∴∠BCP=30°，
∴∠AEB=60°，
∴∠PEC=180°-∠AEB=120° .
点睛：本题考查了正方形的性质，勾股定理，全等三角形的判定与性质，两点之间线段最短及分类讨论的数学思想，运用勾股定理是解（1）的关键，确定点P的位置是解（2）的关键，分两种情况讨论是解（3）的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（）1．
【解析】
首先求出AC、AE、HE的长度，然后猜测命题中隐含的数学规律，即可解决问题．
【详解】
∵四边形ABCD为正方形，
∴AB=BC=1，∠B=90°，
∴AC2=12+12，AC=；
同理可求：AE=（）2，HE=（）3…，
∴第n个正方形的边长an=（）n-1，
∴第2016个正方形的边长为（）1，
故答案为（）1．
本题考查了勾股定理在直角三角形中的运用，考查了学生找规律的能力，本题中找到an的规律是解题的关键．
20、y=﹣x+
【解析】
在Rt△OAB中，OA=4，OB=3，用勾股定理计算出AB=5，再根据折叠的性质得BA′=BA=5，CA′=CA，则OA′=BA′﹣OB=2，设OC=t，则CA=CA′=4﹣t，在Rt△OA′C中，根据勾股定理得到t2+22=（4﹣t）2，解得t=，则C点坐标为（0，），然后利用待定系数法确定直线BC的解析式
【详解】
解：∵A（0，4），B（3，0），
∴OA=4，OB=3，
在Rt△OAB中，AB==5，
∵△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，
∴BA′=BA=5，CA′=CA，
∴OA′=BA′﹣OB=5﹣3=2，
设OC=t，则CA=CA′=4﹣t，
在Rt△OA′C中，
∵OC2+OA′2=CA′2，
∴t2+22=（4﹣t）2，解得t=，
∴C点坐标为（0，），
设直线BC的解析式为y=kx+b，
把B（3，0）、C（0，）代入得，解得
∴直线BC的解析式为y=﹣x+
故答案为y=﹣x+．
【考点】
翻折变换（折叠问题）；待定系数法求一次函数解析式．
21、
【解析】
解：∵∠A=90°，∴∠ABC+∠ACB=90°，∵角平分线BE、CF交于点O，∴∠OBC+∠OCB=45°，∴∠BOC=180°﹣45°=135°．故答案为：135°．
点睛：本题考查了角平分线的定义、三角形的内角和定理：三角形的内角和等于180°．
22、1
【解析】
利用向量的三角形法则直接求得答案．
【详解】
如图：
∵-==且||=1，
∴||=1．
故答案为：1．
此题考查了平面向量，属于基础题，熟记三角形法则即可解答．
23、矩形的对角线相等
【解析】
根据逆命题的定义：对于两个命题，如果一个命题的条件和结论分别是另外一个命题的结论和条件，那么这两个命题叫做互逆命题，其中一个命题叫做原命题，另外一个命题叫做原命题的逆命题，原命题的条件是对角线相等，结论是矩形，互换即可得解.
【详解】
原命题的条件是：对角线相等的四边形，结论是：矩形；
则逆命题为矩形的对角线相等.
此题主要考查对逆命题的理解，熟练掌握，即可解题.
二、解答题（本大题共3个小题，共30分）
24、（1），;(3) ①理由详见解析；②;(3) 3﹣或或3+．
【解析】
试题分析：(1)根据两点之间,线段最短可知,点Q在线段BD上时BQ＋DQ的值最小,是BD的长度,利用勾股定理即可求出;再根据△PDQ是等腰直角三角形求出x的值;
(3) ①由对称可知AB=BQ=BC,因此∠BCQ=∠BQC.根据∠BQE=∠BCE=90°,可知∠EQC=∠ECQ,从而EQ=EC.再根据∠CQD=90°可得∠DQE+∠CQE=90°, ∠QCE+∠QDE=90°,而∠EQC=∠ECQ, 所以∠QDE=∠DQE，从而EQ=ED.易得点E是CD的中点；②在Rt△PDE中，PE= PQ+QE=x+，PD=1﹣x，PQ=x，根据勾股定理即可求出x的值.
(3) △CDQ为等腰三角形分两种情况:①CD为腰,以点C 为圆心,以CD的长为半径画弧,两弧交点即为使得△CDQ为等腰三角形的Q点; ②CD为底边时,作CD的垂直平分线,与的交点即为△CDQ为等腰三角形的Q点,则共有 3个Q点,那么也共有3个P点,作辅助线,利用直角三角形的性质求之即得.
试题解析：（1），．
（3）①证明：在正方形ABCD中，
AB=BC，∠A=∠BCD=90°．
∵Q点为A点关于BP的对称点，
∴AB=QB，∠A=∠PQB=90°，
∴QB=BC，∠BQE=∠BCE，
∴∠BQC=∠BCQ，
∴∠EQC=∠EQB﹣∠CQB=∠ECB﹣∠QCB=∠ECQ，
∴EQ=EC．
在Rt△QDC中，
∵∠QDE=90°﹣∠QCE，
∠DQE=90°﹣∠EQC，
∴∠QDE=∠DQE，
∴EQ=ED，
∴CE=EQ=ED，即E为CD的中点．
②∵AP=x，AD=1，
∴PD=1﹣x，PQ=x，CD=1．
在Rt△DQC中，
∵E为CD的中点，
∴DE=QE=CE=，
∴PE=PQ+QE=x+，
∴，
解得 x=．
（3）△CDQ为等腰三角形时x的值为3-，，3+．
如图，以点B为圆心，以AB的长为半径画弧，以点C为圆心，以CD的长为半径画弧，两弧分别交于Q1，Q3．此时△CDQ1，△CDQ3都为以CD为腰的等腰三角形．作CD的垂直平分线交弧AC于点Q3，此时
△CDQ3以CD为底的等腰三形．
以下对此Q1，Q3，Q3．分别讨论各自的P点，并求AP的值．
讨论Q₁:如图作辅助线，连接BQ1、CQ1，作PQ1⊥BQ1交AD于P，过点Q1，作EF⊥AD于E，交BC于F．
∵△BCQ1为等边三角形，正方形ABCD边长为1，
∴，．
在四边形ABPQ1中，
∵∠ABQ1=30°，
∴∠APQ1=150°，
∴△PEQ1为含30°的直角三角形，
∴PE=．
∵AE=，
∴x=AP=AE-PE=3-．
②讨论Q3，如图作辅助线，连接BQ3，AQ3，过点Q3作PG⊥BQ3，交AD于P，连接BP，过点Q3作EF⊥CD于E，交AB于F．

∵EF垂直平分CD，
∴EF垂直平分AB，
∴AQ3=BQ3．
∵AB=BQ3，
∴△ABQ3为等边三角形．
在四边形ABQP中，
∵∠BAD=∠BQP=90°, ∠ABQ₂=60°,
∴∠APE=130°
∴∠EQ3G=∠DPG=180°-130°=60°，
∴，
∴EG=，
∴DG=DE+GE=-1，
∴PD=1-，
∴x=AP=1-PD=．
③对Q3，如图作辅助线，连接BQ1，CQ1，BQ3，CQ3，过点Q3作BQ3⊥PQ3，交AD的延长线于P，连接BP，过点Q1，作EF⊥AD于E，此时Q3在EF上，不妨记Q3与F重合．

∵△BCQ1为等边三角形，△BCQ3为等边三角形，BC=1，
∴，，
∴．
在四边形ABQ3P中
∵∠ABF=∠ABC+∠CBQ3=150°，
∴∠EPF=30°，
∴EP=,EF=．
∵AE=，
∴x=AP=AE+PE=+3．
综上所述，△CDQ为等腰三角形时x的值为3﹣，，3+．
考点：⒈四边形综合题; ⒉正方形的性质; ⒊等腰三角形的性质.
25、（1），；（2）；（3）或
【解析】
（1）将点代入到直线中，即可求出b的值，然后将点P的坐标代入直线中即可求出m的值；
（2）根据图象即可得出结论；
（3）分别用含a的式子表示出点C和点D的纵坐标，再根据CD的长和两点之间的距离公式列出方程即可求出a．
【详解】
解：（1）∵点在直线上
∴
∵点在直线上，
∴
∴
（2）由图象可知：当时，；
（3）当时，，当时，
∵
∴
解得或
此题考查的是一次函数的图象及性质，掌握根据直线上的点求直线的解析式、一次函数与一元一次不等式的关系和直角坐标系中两点之间的距离公式是解决此题的关键．
26、 (1)详见解析(2)
【解析】
(1) 题干中由且可知，一组对边平行且相等的四边形是平行四边形，则四边形BCDE是平行四边形，又知BE是直角三角形斜边的中线，直角三角形斜边的中线等于斜边的一半，则得到BE=ED，从而再用一组邻边相等的平行四边形是菱形证明即可.
(2)通过 DE∥BC和 AC平分，可得到∠BAC=∠ACB，从而由等角对等边得到AB=BC=1，则此时直角三角形ABD，有一个执教不是斜边的一半，则可知这个直角边对应的角是30°，找到30°才是题目的突破口，然后依次得到角度的关系，证明得到三角形ACD是直角三角形，再用勾股定理解得AC的长.
【详解】
(1)证明：∵DE∥BC且DE=BC（已知）
∴四边形BCDE是平行四边形（一组对边平行且相等的四边形是平行四边形）
又∵E为直角三角形斜边AD边的中点（已知）
∴BE=AD，即BE=DE（直角三角形斜边的中线等于斜边的一半）
∴平行四边形四边形BCDE是菱形（一组邻边相等的平行四边形是菱形）
(2)
连接AC，如图可知：
∵DE∥BC（已知）
∴∠DAC=∠ACB（两直线平行内错角相等）
又∵AC平分（已知）
∴∠BAC=∠DAC（角平分线的定义）
即∠BAC=∠ACB（等量代换）
∴AB=BC=1（等角对等边）
由(1)可知：AD=2ED=2BC=2
在直角三角形中AB=1，AD=2
∴∠ADB=30°（直角三角形中，若一个直角边是斜边 一半，则这个直角边所对的角是30°）
∴∠BAD=60°（直角三角形两锐角互余）
即∠CAD=∠BAD=30°（角平分线的定义），∠ADC=2∠ADB=60°（菱形的性质）
所以三角形ADC是直角三角形.
则由可知：
本题为综合性的几何证明试题，运用到的重点知识点有，菱形的判定定理，菱形的性质，直角三角形斜边中线定理，30°角定理，勾股定理，注意证明过程中，条理清楚，因果对应，灵活运用才是解题关键.
题号
一
二
三
四
五
总分
得分
甲种货车
乙种货车
方案一
2辆
6辆
方案二
3辆
5辆
方案三
1辆
1辆