初中人教版（2024）第十三章 轴对称13.3 等腰三角形13.3.1 等腰三角形优秀一课一练

这是一份初中人教版（2024）第十三章 轴对称13.3 等腰三角形13.3.1 等腰三角形优秀一课一练，文件包含专题1314等腰三角形七种常见辅助线作法方法梳理与题型分类讲解人教版原卷版docx、专题1314等腰三角形七种常见辅助线作法方法梳理与题型分类讲解人教版解析版docx等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。

题型目录
【题型1】作等腰三角形底边上高线求值或证明
【题型2】遇到中点作中线求值或证明
【题型3】过一腰上的某一已知点作另一腰的平行线
【题型4】过一腰上的某一已知点作底边的平行线
【题型5】倍长中线构造等腰三角形
【题型6】截长补短构造等腰三角形
【题型7】延长相交构造或证明等腰三角形
第二部分【题型展示与方法点拨】
【题型1】作等腰三角形底边上高线求值或证明
【例1】（2024·浙江·模拟预测）如图，是等腰三角形，．设．
(1)如图1，点D在线段上，若，求的度数（用含的代数式表示）．
(2)如图2，已知．若，过点B作于点H，求证：．
【答案】(1) (2)见解析
【分析】本题主要考查了等腰三角形的判定和性质，角平分线的性质定理，
（1）根据等腰三角形的性质可得，设，，解出方程组，即可求解；
（2）延长，交于点F，过点A作于点E．根据，可得 ．再由等腰三角形的性质可得 ，从而得到，，进而得到，然后根据角平分线的性质定理，可得，即可求证．
解：（1）∵，
∴．
设，，则
解得：，
即；
（2）如图，延长，交于点F，过点A作于点E．
∵，．
∴．
又∵，
∴
∵，
∴，
∴．
又∵，，
∴，
∴．
【变式1】（24-25八年级上·全国·课后作业）如图，在中，，平分交于点，是上一点，且．求证：．

【分析】本题主要考查了等腰三角形的性质，角平分线的定义，全等三角形的判定和性质，正确作出辅助线，构建全等三角形是解题的关键．
作于点，根据等腰三角形的性质得出，再证明即可得出结论．
证明：如图，作于点．

，
．
，
．
平分，
．
在和中，
，
，
，
．
【变式2】（22-23八年级上·江苏泰州·阶段练习）在中，，过点C作射线，使（点与点B在直线的异侧）点D是射线上一动点（不与点C重合），点E在线段上，且．
(1)如图1，当点E与点C重合时，与的位置关系是 ，若，则的长为 ；（用含a的式子表示）
(2)如图 2，当点 E 与点 C 不重合时，连接 ，
①若，求 的度数；
②用等式表示与直间的数量关系，并证明．
【答案】(1)互相垂直； (2)①；②
【分析】（1）根据三角形内角和定理可得与的位置关系是互相垂直，过点A作于点M，根据等腰三角形性质得到，利用证明，根据全等三角形性质即可得出；
（2）当点E与点C不重合时，①求解，可得，由，可得，可得；②过点A作于点M、于点N，利用证明，根据全等三角形性质即可得到；
解：（1）当点E与点C重合时，，
∵，
∴，
∴，
∴，
即与的位置关系是互相垂直，
若，过点A作于点M，如图：

则，
∵，
∴，
在与中，
∴，
∴，
即的长为，
（2）解：①∵，，
∴，
∴，
∵，
∴，
∴；
②当点E与点C不重合时，用等式表示与之间的数量关系是：，证明如下：
过点A作于点M、于点N，如图：

则，
∴，
∵，
即，
∴，
∵，，
∴，
在与中，
，
∴，
∴，
∴；
【点拨】本题是三角形综合题，考查了等腰三角形的性质、全等三角形的判定与性质、三角形内角和定理、垂直定义等知识，熟练掌握等腰三角形的性质、全等三角形的判定与性质并作出合理的辅助线是解题的关键．
【题型2】遇到中点作中线求值或证明
【例3】（23-24七年级下·四川成都·阶段练习）在中，，且的顶点E在边上移动，在移动过程中，边，分别与，交于点M，N，
(1)当且M与A重合时，求证：
(2)当E为中点时，连接，求证：
【分析】本题考查等腰三角形的性质、全等三角形的判定与性质、三角形外角的性质，
（1）根据等腰直角三角形的性质可得，利用三角形外角的性质与等量代换可得，在根据全等三角形的判定即可证明；
（2）连接，在上截取，根据等腰直角三角形的性质可得，，证得，可得，，利用等量代换可得，证得，可得，即可得证．
解：（1）证明：∵，，
∴，
∵，
又∵，
∴，
又∵，
∴；
（2）证明：连接，在上截取，
∵，，E为中点，
∴，，
∴，
在和中，
，
∴，
∴，，
∵，
∴，即，
∵，
∴，
又∵，，
∴，
∴，
∵，
∴．
【变式1】（23-24八年级上·广东汕头·期中）如图，中，，是的中点，、分别是、上的点，且，求证：．

【分析】本题考查了等腰三角形的性质和全等三角形的判定和性质，属于基础题目，熟练掌握上述知识是解题的关键．
连接，根据等腰三角形的性质可得，然后即可证明，进而可得结论．
证明：连接，
，是的中点，
∴，
在和中，
，
，
．

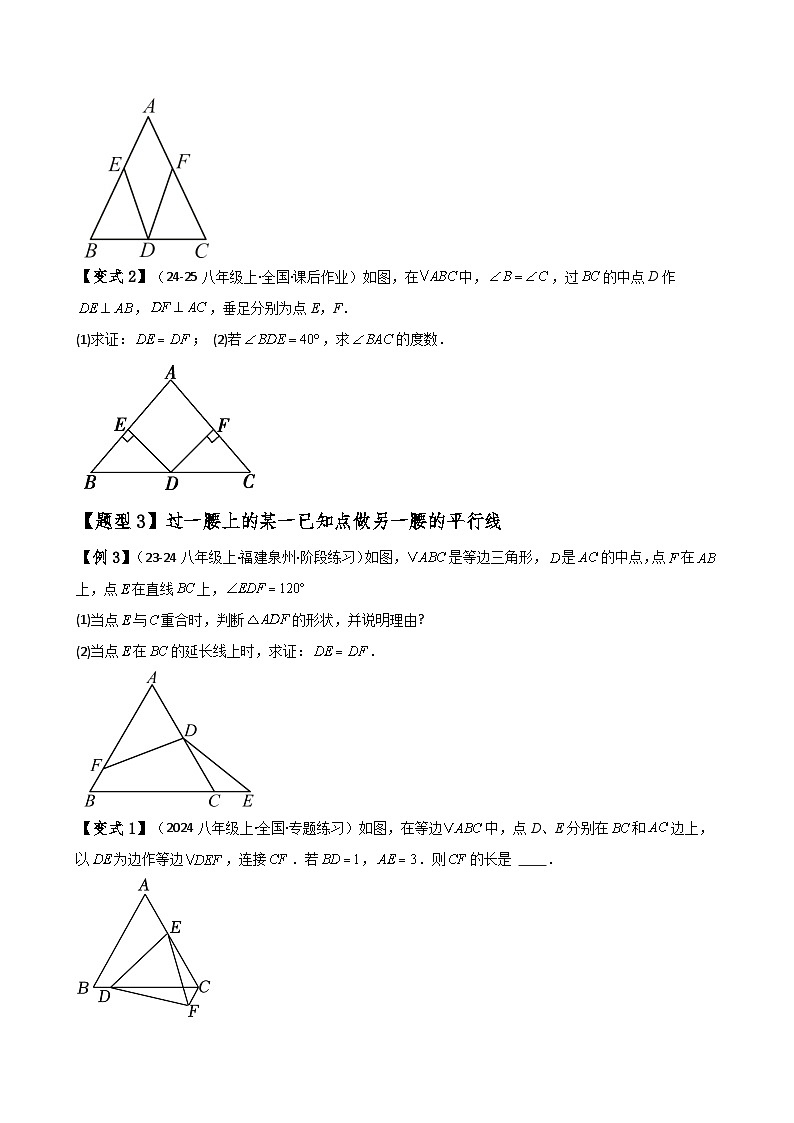
【变式2】（24-25八年级上·全国·课后作业）如图，在中，，过的中点D作，，垂足分别为点E，F．
(1)求证：； (2)若，求的度数．
【答案】(1)见解析；(2)。
【分析】本题考查了全等三角形的判定和性质，等腰三角形的判定和性质．
（1）通过证明，即可求证；
（2）连接，易得，则AD平分，，根据．推出，即可解答．
（1）证明：∵，，
∴．
∵D是的中点，
∴．
在和中，
∴．
∴．
（2）解：连接．
∵，
∴，
∵D是的中点，
∴AD平分，，
∴．
∴．
∴．
【题型3】过一腰上的某一已知点作另一腰的平行线
【例3】（23-24八年级上·福建泉州·阶段练习）如图，是等边三角形，是的中点，点在上，点在直线上，
(1)当点与重合时，判断的形状，并说明理由?
(2)当点在的延长线上时，求证：．
【答案】(1)等边三角形，证明见详解 (2)证明过程见详解
【分析】本题考查等边三角形的性质，全等三角形的判定，熟练掌握全等三角形的判定方法是解题的关键．
（1）根据，得，从而证明，即可证明是等边三角形；
（2）过点作交于点，证明，即可求解；
解：（1）根据题意作图如下：
，
为等边三角形
，
，
为等边三角形．
（2）证明：过点作交于点，
是等边三角形，
，，
，
，
，，
又，
为等边三角形
，，
，
，
即，
点是的中点，
，
，
在和中，
，
．
【变式1】（2024八年级上·全国·专题练习）如图，在等边中，点D、E分别在和边上，以为边作等边，连接．若，．则的长是 ．
【答案】2
【分析】本题考查的是的是等边三角形的判定与性质，全等三角形的判定与性质，作出合适的辅助线是解本题的关键．
过D点作于M，证明为等边三角形，再证明，结合全等三角形的性质可得答案．
解：∵等边，
∴，，
过D点作于M，
∴，，
∴为等边三角形，
∴， ，
∴，

∵为等边三角形，
∴，，
∴，
∴，
∴，
∵，．
∴．
∴．
故答案为：2．
【变式2】（22-23八年级下·广西南宁·开学考试）如图，等边三角形中，D为上一点，E为延长线上一点，交于点F，且．若，则的长为 ．
【答案】4
【分析】本题主要考查了等边三角形的性质与判定，全等三角形的性质与判定，三角形内角和定理，三角形外角的性质，作，交于M，得为等边三角形，再证得到；根据，，可得，由此得出，最后根据即可求得的长．
解：如图，作，交于M，
∴，，，
∵是等边三角形，
∴，
∴，
∴是等边三角形，
∴，
在和中，
，
∴.
∴，，
∵，，
∴，
∴
∴，
∴，
又∵，
∴，
故答案为：4．
【题型4】过一腰上的某一已知点作底边的平行线
【例4】（23-24八年级上·湖南怀化·期末）如图，在等边中，点M为上任意一点，延长至点N，使，连接交于点P．
(1)求证：；
(2)作于点H，设，请用含的式子表示的长度．
【答案】(1)证明见解析 (2)
【分析】本题考查了等边三角形的性质、平行线的性质、全等三角形的判定及性质，
（1）在等边中过点作与交于，先根据平行线的性质得出，，再根据等边三角形的性质得出，然后利用证明，最后根据全等三角形的性质即可得证；
（2）根据等腰三角形的三线合一得出是的中点，再利用全等三角形的性质得出，然后利用线段的和与差即可得出答案．
解：（1）证明：如图，在等边中过点作与交于，

∴，，
∵是等边三角形，
∴，
∴是等边三角形，
∴，
又∵，
∴，
在与中，
，
，
；
（2）∵于点，且是等边三角形，
∴是的中点，
又∵由（1）知，
∴ ，
∴，
∵，
∴．
【变式1】（23-24七年级下·陕西榆林·阶段练习）阅读下面的题目及分析过程，并按要求进行证明．如图，已知E是的中点，点A在上，且．求证：．
(1)现给出如下两种添加辅助线的方法，请任意选出其中一种，对原题进行证明．
①如图1，延长到点F，使，连接；
②如图2，过点B作，交的延长线于点F，过点C作，垂足为G．
请你在图3中添加不同于（1）中的辅助线，并对原题进行证明．

【答案】(1)①见解析；②见解析；(2)见解析
【分析】此题考查了全等三角形的判定和性质，添加辅助线构造全等三角形是解题的关键．
（1）①证明，则，由得到，则，即可证明结论；②证明，则，再证明，即可得到结论；
（2）过点C作，交的延长线于点M，则，证明，则，由，得到，则，即可证明结论．
解：（1）证明：①如图1，延长到点F，使，连接
∵E是的中点，
∴
在和中，
，
∴，
∴，
∵,
∴，
∴，
∴；
②如图2，过点B作，交的延长线于点F，过点C作，垂足为G．
∵E是的中点，
∴
∵，，
∴，
在和中，
，
∴，
∴，
在和中，
，
∴，
∴，
（2）如图，过点C作，交的延长线于点M，则，
∵E是的中点，
∴
在和中，
，
∴，
∴，
∵，，
∴，
∴，
∴
【变式2】（21-22八年级上·湖北武汉·期中）如图，在等边三角形中，点D在上，延长至点E，使于点F．
(1)如图①，若点D是的中点，求证：；
(2)如图②，若点D是上任意一点，是否仍然成立？请证明你的结论；
(3)如图③，若点D是延长线上的任意一点，其他条件不变，（2）中的结论是否仍然成立？画图并写出你的结论，不必证明．
【答案】(1)见解析 (2)仍然成立，证明见解析 (3)（2）中的结论仍然成立，图见解析
【分析】此题考查了等边三角形的性质，三线合一，全等三角形的判定和性质，
（1）根据等边三角形得到，，三线合一推出，证得，，而证得，利用三线合一证得；
（2）过点D作，交于点M，得到是等边三角形，由此证明，得到，根据三线合一证得；
（3）过点E作，交的延长线于点N，得到等边三角形，证明，得到，根据三线合一证得．
解：（1）证明：∵是等边三角形，
∴，
∵点D是的中点，
∴，，
∵，
∴，
∴，
∴，
∴
∵，
∴；
（2）仍然成立，
证明：过点D作，交于点M，
∴，，
∴是等边三角形，
∴，
∴，即，
∵，，
∴，
∴，
∴，
∵，
∴；
（3）（2）中的结论仍然成立，
证明：如图，过点E作，交的延长线于点N，
∴，，
又∵，
∴是等边三角形，
∴，
∵，
∴，，
∴，
∴，
∴，
∴，
∵，
∴．
【题型5】倍长中线构造等腰三角形
【例5】（22-23八年级上·湖北武汉·期中）如图，在中，D是的中点，E是上一点，，的延长线交于点F，若，，则求的度数为 ．

【答案】/32度
【分析】本题考查了全等三角形的判定和性质，等腰三角形的性质，正确的作出辅助线构造全等三角形是解题的关键．延长到G使，连接，通过，根据全等三角形的性质得到，，等量代换得到，由等腰三角形的性质得到，即可得到，进而利用三角形内角和解答即可．
解：如图，延长到G使，连接，

在与中，
∴，
∴，，
∵，
∴，
∴，
∵，
∴，
∵，，
∴，，
∴，
故答案为：
【变式1】（23-24七年级下·黑龙江哈尔滨·阶段练习）如图在四边形中，是的中点，连接，平分，，，则线段的长为 ．
【答案】/
【分析】本题考查了全等三角形的判定和性质，等腰三角形的判定和性质，作辅助线构造全等三角形是解题关键．延长、交于点，证明，得到，，结合角平分线的定义，得到，进而得到，求出的长即可求解．
解：如图，延长、交于点，
是的中点，
，
在和中，
，
，
，，
平分，
，
，
，
，
，
，
，
故答案为：
【变式2】（24-25八年级上·陕西西安·开学考试）小明同学在学习完全等三角形后，发现可以通过添加辅助线构造全等三角形来解决问题．
(1)如图（1），是的中线，且，延长至点，使，连接，可证得，其中判定两个三角形全等的依据为________．
(2)如图（2），在中，点在上，且，过作，且．求证：平分．
【答案】(1)；(2)见解析.
【分析】本题考查全等三角形的判定和性质，等腰三角形的判定和性质，掌握倍长中线法构造全等三角形，是解题的关键．
（1）根据全等三角形的判定方法，进行作答即可；
（2）延长至，使得，连接，先证明，得到，，平行线的性质，得到，等量代换结合等边对等角，得到，再利用等量代换，得到，即可．
解：（1）∵是的中线，
∴，
∴，，
∴，
故答案为：；
（2）证明：如图，延长至，使得，连接，
在和中，
，
∴，
∴，，
∵，
∴，
又∵．
∴，
∴，
∴，
∴平分
【题型6】截长补短构造等腰三角形
【例6】（23-24八年级上·广东深圳·期末）如图，在中，，，三角形内有一点，连接，，，若平分，，则 ．

【答案】/度
【分析】如图所示，延长到H使得，连接，先求出，再由等边对等角和三角形内角和定理得到，则，可推出，证明，得到，再求出，，进而证明是等边三角形，推出，则．
解：如图所示，延长到H使得，连接，
∵，，
∴，
∵，
∴，
∴，
∴，
∵平分，
∴，
又∵，
∴ ，
∴，
∵，
∴，，
∴是等边三角形，
∴，
∴，
∴，
故答案为：．
【点拨】本题主要考查了等边三角形的性质与判定，全等三角形的性质与判定，等边对等角，三角形内角和定理，三角形外角的性质等等，通过作出辅助线证明是解题的关键．
【变式1】（23-24八年级上·江苏南京·期末）如图，在中，，平分交于点D，点E在的延长线上，，若，则线段的长为 ．
【答案】4
【分析】如图，在上截取，使，连接，证明，则，，，由，可得，则，计算求解即可．
解：如图，在上截取，使，连接，
∵，
∴，
∵平分，
∴，
∵，
∴，
∴，
∵，
∴，
∴，，
∴，
∵，
∴，
∴，
故答案为：4．
【点拨】本题考查了等腰三角形的判定与性质，角平分线，全等三角形的判定与性质，三角形内角和定理等知识．熟练掌握等腰三角形的判定与性质，角平分线，全等三角形的判定与性质，三角形内角和定理是解题的关键．
【变式2】（2024·陕西西安·三模）如图，是等边三角形，D为外一点，且，连接，若，则的长为 ．
【答案】
【分析】本题考查了全等三角形的的判定与性质、等边三角形的判定与性质，掌握其性质定理是解决此题的关键．在上截取，连接，根据等边三角形的判定与性质可得，再利用全等三角形的判定与性质可得结论．
解：证明：在上截取，连接，如图所示，
，
为等边三角形，
，，
为等边三角形，
，，
，
，
，
，
．
故答案为：．
【题型7】延长相交构造或证明等腰三角形
【例7】（23-24八年级上·福建泉州·阶段练习）如图，在中，，，动点在射线上，交于，的平分线交于．则当时， ．
【答案】
【分析】本题考查了平行线的性质，角平分线的定义，等角对等边，全等三角形的判定和性质，延长交于点，由平行线的性质可得，由角平分线的定义可得，得到，即得，进而得到，再证明，得到，据此即可求解，正确作出辅助线是解题的关键．
解：延长交于点，
∵，
∴，
∴，
∵平分，
∴，
∴，
∴，
∴，
∵，
∴，
在和中，
，
∴，
∴，
∴，
故答案为：．
【变式1】（23-24八年级下·黑龙江哈尔滨·开学考试）如图，为外一点，，BD平分的一个外角，若，，，则AD的长为 ．
【答案】4
【分析】本题主要考查等腰三角形的判定和性质，全等三角形的判定和性质，角平分线的性质，掌握等角对等边是解题的关键．
延长交于点，根据角平分线的性质，垂直的性质可证，可得，根据三角形内角和定理可得，，由此即可求解．
解：如图所示，延长交于点，
∵BD平分，，
∴，，BD是公共边，
∴，
∴，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
故答案为：4．
【变式2】（23-24九年级下·山东临沂·期中）如图，，，点E为的中点，若，，，则的长为 ．
【答案】3
【分析】本题主要考查了全等三角形的性质与判定，等边三角形的性质与判定，如图所示，延长交于F，证明，得到，，再证明是等边三角形，得到，则．
解：如图所示，延长交于F，
∵，
∴，
∵点E为的中点，
∴，
∴，
∴，，
∴，
∴，
又∵，
∴是等边三角形，
∴，
∴，
故答案为：3．