初中数学13.3.2 等边三角形优秀课时练习

这是一份初中数学13.3.2 等边三角形优秀课时练习，共30页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．（24-25八年级上·全国·假期作业）如图，是等边三角形，为中线，为上一点，且，则等于（ ）
A．B．C．D．
2．（23-24八年级下·辽宁朝阳·期末）如图，是等边三角形的边的中点，是边延长线上一点，，则的度数是（ ）
A．B．C．D．
3．（22-23八年级上·江西上饶·阶段练习）下列对的判断，错误的是（ ）
A．若，，则是等边三角形
B．若，则是直角三角形
C．若，，则是等腰三角形
D．若，，则
4．（23-24七年级下·山东淄博·期末）如图，，以点O为圆心，任意长为半径画弧，分别交，于点A，D，再以点A为圆心，长为半径画弧，与弧交于点B，连接、，的延长线交于点C，若，则的长为（ ）
A．3B．4C．5D．6
5．（2024·山东·模拟预测）如图，两块三角板、按如图所示方式摆放，且，连接，若，，则四边形的面积为（ ）
A．9B．11C．D．
6．（23-24八年级下·广东深圳·阶段练习）如图，已知，点，…在射线上，点，…在射线上，，，，…均为等边三角形，若，则的边长是（ ）
A．4046B．4048C．D．
7．（2024·山东聊城·模拟预测）如图，在中，，，以点为圆心，以的长为半径画弧交于点，连接，再分别以点，为圆心，大于的长为半径画弧，两弧交于点，作射线交于点，交于点，连接，则的值是（ ）
A．B．C．D．
8．（23-24八年级下·江西九江·期末）如图，在等腰中，顶角，点D为边上的一点，，点E为上一点，，则的度数为（ ）

A．B．C．D．
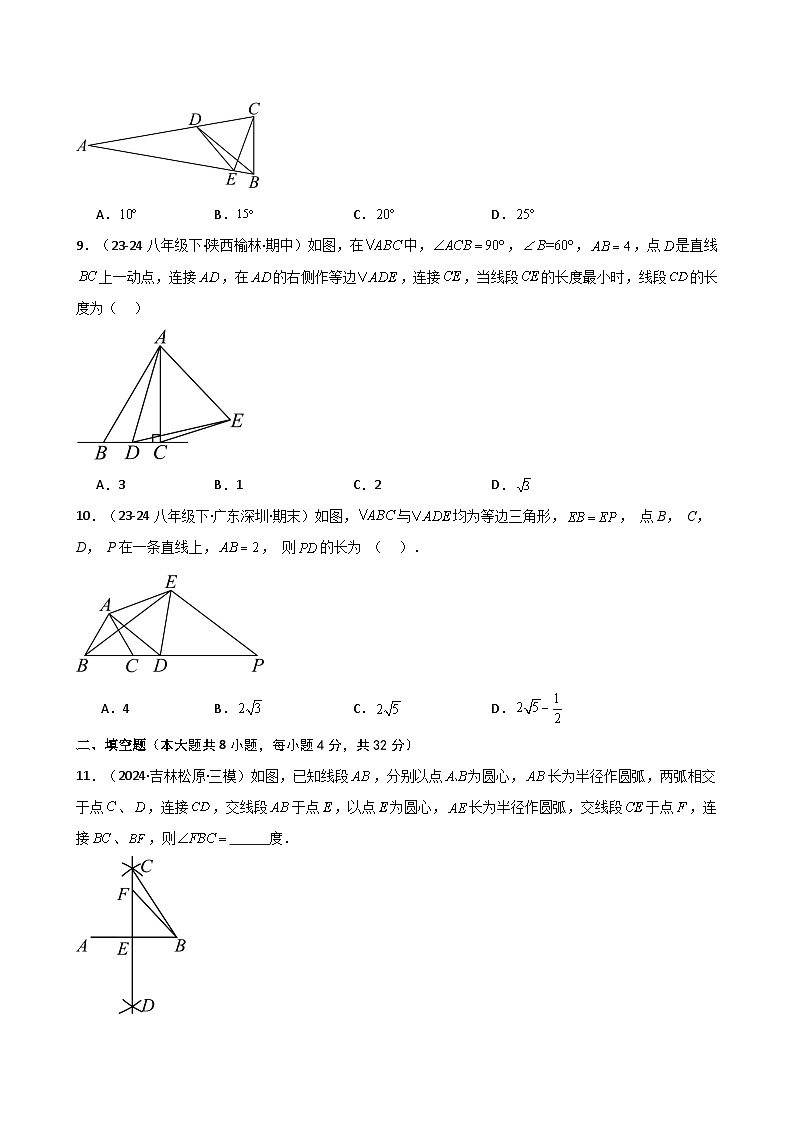
9．（23-24八年级下·陕西榆林·期中）如图，在中，，，，点是直线上一动点，连接，在的右侧作等边，连接，当线段的长度最小时，线段的长度为（ ）
A．3B．1C．2D．
10．（23-24八年级下·广东深圳·期末）如图，与均为等边三角形，， 点B， C， D， P在一条直线上，， 则的长为 （ ）．

A．4B．C．D．
二、填空题（本大题共8小题，每小题4分，共32分）
11．（2024·吉林松原·三模）如图，已知线段，分别以点为圆心，长为半径作圆弧，两弧相交于点、，连接，交线段于点，以点为圆心，长为半径作圆弧，交线段于点，连接、，则 度．
12．（23-24七年级下·四川成都·期末）如图，在等边中，平分，点E是延长线上一点，且，连接，则 ．
13．（23-24八年级上·江苏连云港·期末）已知：如图，在中，，，于点，且，则是 三角形．

14．（23-24八年级下·辽宁沈阳·期末）将含角的直角三角板和直尺按如图所示的方式放置，已知，点B，点C表示的刻度分别为，则的周长为 ．
15．（23-24八年级上·浙江杭州·开学考试）如图，等边三角形中，D、E分别为边上的两动点，与交于点F，于点G，若，则 ．
16．（23-24七年级下·河南洛阳·期末）如图，将长方形纸片对折，使与重合，展平纸片，得到折痕；折叠纸片，使点B落在上，并使折痕经过点A，得到折痕，点B，E的对应点分别为G，H，展平纸片，连结，，则与的关系是 ．
17．（23-24八年级上·浙江台州·期末）一副三角板如图叠放，，，互相平分于点O，点F在边上，边交于点H，边交于点G．
（1） ；
（2）若，则 （用含a的代数式表示）．

18．（23-24八年级上·河北保定·期末）（1）如图1，，都是等边三角形，线段和之间的数量关系为 ．
（2）如图2，，垂足为O，，B为直线上一动点，以为边向右作等边，则线段的最小值为 ．
三、解答题（本大题共6小题，共58分）
19．（8分）（23-24七年级下·辽宁朝阳·期末）已知，均为等边三角形，点是内的任意一点，
(1)如图，试说明
(2)当为等腰直角三角形时，________（直接写答案）
20．（8分）（22-23八年级上·重庆丰都·期末）如图，点E在的外部，点D在上，交于点F，，，．
(1)求证：．
(2)若，猜想的形状并证明．
21．（10分）（23-24七年级下·山东威海·期末）如图，在中，，，，点D从点A以的速度向点C运动，同时点E从点C以的速度向点B运动，运动时间为．
(1)当t= 时，为等边三角形；（直接写结果）
(2)当t为何值时，为直角三角形？
22．（10分）（23-24八年级下·四川成都·阶段练习）是等边三角形，点是边上动点，，把沿对折，得到．
(1)如图1，若，则____．
(2)如图2，点在延长线上，且，连接，若，，三点共线．
①求证：平分；
②若，，求的长．
23．（10分）（23-24八年级下·陕西咸阳·阶段练习）如图，，与相交于点E，．

(1)求证：AC垂直平分BD；
(2)如图2，过点B作交的延长线于点F，若；
①求证：是等边三角形；
②如果G、H分别是线段、线段上的动点，当的值最小时，写出此时与的数量关系，并说明理由．
24．（12分）（23-24八年级上·安徽阜阳·期末）在等腰中，，点是上一动点，点在的延长线上，且，平分交于点，连接．
(1)如图1，求证：；
(2)如图2，当时，在上取点，使，连接．求证：是等边三角形；
(3)如图3，当，且时，求证：．
参考答案：
1．A
【分析】本题主要考查等边三角形的性质，三角形的内角和定理，等腰三角形的性质，由等边三角形的性质可求解，，利用等腰三角形的性质及三角形的内角和定理可得的度数，进而可求解．
【详解】解：为等边三角形，
，
是等边三角形的中线，
，，
，
，
，
，
，
故选：．
2．B
【分析】本题主要考查了等边三角形的性质，“三线合一”以及三角形外角的定义和性质等知识，掌握“三线合一”是解答本题的关键．根据“三线合一”可得平分，可得，根据即可作答．
【详解】∵是等边三角形的边的中点，
∴平分，，
∴，
∵，
∴，
∴，
故选：B．
3．D
【详解】解：A.，，
是等边三角形，故该选项正确；
B.，
最大角为：，
是直角三角形，故该选项正确；
C.，，
，
是等腰三角形，故该选项正确；
D.，，
，故该选项错误；
故选：D
【点拨】本题考查了等腰三角形、等边三角形、直角三角形的判定及性质，熟练掌握和运用各图形的判定与性质是解决本题的关键
4．B
【分析】由题意得，则可得是等边三角形，则，进而可得，则可得．
本题主要考查这了等边三角形的判定和性质、等腰三角形的判定和性质．熟练掌握以上知识是解题的关键．
【详解】解：由题意得，
是等边三角形，
，
，
，
，
．
故选：B
5．D
【分析】本题考查直角三角形性质，等腰直角三角形性质，平行线的判定，以及梯形面积公式，利用直角三角形性质得到，利用等腰三角形性质得到，证明，进而得到四边形是直角梯形，再利用梯形的面积公式求解，即可解题．
【详解】解：由题知，，，
，
由题知，，，，
，
，
，
四边形是直角梯形，
则四边形的面积为．
故选：D．
6．C
【分析】本题考查的是等边三角形的性质、三角形的外角性质，等腰三角形的判定及其性质，总结出规律是解题的关键．根据等边三角形的性质得到，根据三角形的外角性质求出，得到，根据等腰三角形的判定定理得到，然后找到规律即可得解．
【详解】∵为等边三角形，
∴，
∴，
∴，
∴，
同理可得，，
……，
∴的边长为．
故选：C．
7．D
【分析】先根据角的直角三角形的性质得到，证明，再根据全等三角形的判定和性质定理即可得到结论．
【详解】解：∵，，
∴，
∴，
由题意得：，平分，
∴，
在与中，
，
∴，
∴，
∵，
∴，
∴，
∴，
∴．
故选：D．
【点拨】本题考查作图—基本作图，直角三角形两锐角互余，角的直角三角形，全等三角形的判定和性质，角平分线的定义，等底同高的三角形面积相等．掌握基本作图及全等三角形的判定和性质是解题的关键．
8．A
【分析】本题主要考查了等腰三角形的判定与性质，三角形内角和定理，等边三角形的判定与性质等知识，先根据等腰三角形的性质求出，再由三角形内角和定理得，可得，再由三角形内角和定理求出 ，，得，即可得是等边三角形，可求出，从而可得结论．
【详解】解：∵在等腰中，顶角，
∴，
∴，
∵，
∴，
∵ ，
∴，
∴，
∴，
∵ ，，
∴ ，，
∴，
∴，
∴，
∵，
∴是等边三角形，
∴，
∴，
故选：A
9．A
【分析】本题考查的是等边三角形的性质，全等三角形的判定与性质，垂线段最短，含30度的直角三角形的性质，灵活运用以上知识解题是解题的关键．在的左侧作等边三角形，连接、、、，再证明 可得 再利用时，最短，从而可得答案．
【详解】解： 在的左侧作等边三角形，连接、、、，
则
∴，
∴点、关于对称，
∴，，
均为等边三角形，
，，
，
，
，
∴当时，最小，即此时最小，
∵

∴，
∴的长度为，
故选：A．
10．A
【分析】本题主要考查了等边三角形的性质、全等三角形的判定与性质、等腰三角形的性质等知识点，灵活运用相关判定、性质定理成为解题的关键．
连接，过E作与F，根据等腰三角形的性质可得，再根据等边三角形的性质可得、，进而得到，再证可得；然后说明可得；设，则，然后用x表示出、，然后根据线段的和差即可解答．
【详解】解：如图：连接，过E作与F，
∵，
∴，
∵为等边三角形，
∴，
∵为等边三角形，
∴，
∴，
∴，即，
在和中，，
∴，
∴，
∵，
∴，
∵，
∴，
∴
设，则
∴，
∵，
∴，即，
∴，
∴．
故选A．

11．15
【分析】本题考查了作图—基本作图、等边三角形的性质、等腰直角三角形的性质，由题意得出是等边三角形，为等腰直角三角形，从而得出，，最后再由计算即可得出答案，熟练掌握以上知识点并灵活运用是解此题的关键．
【详解】解：如图，连接．
由作图可知，垂直平分线段，，
∴是等边三角形，为等腰直角三角形，
∴，，
∴．
故答案为：15．
12．/120度
【分析】本题主要考查了等边三角形的性质，等腰三角形的性质，三角形外角的性质．根据等边三角形的性质可得，，再由，可得，然后根据三角形外角的性质可得，即可求解．
【详解】解：∵是等边三角形，
∴，
∵平分，
∴，即，
∵，
∴，
∵，
∴，
∴．
故答案为：．
13．等边
【分析】本题考查等腰三角形的性质和等边三角形的判定，解答时先由三线合一得到，再证明可得到，进而证明为等边三角形．
【详解】解：∵中，，，于点，
∴，，
∵，，
∴
∴，
∵
∴
∵，
∴为等边三角形．
故答案为：等边
14．
【分析】本题考查了平行线的性质，等边三角形的性质与判定，得出是解题的关键．根据平行线的性质得出，进而可得是等边三角形，根据等边三角形的性质即可求解．
【详解】解：∵直尺的两边平行，
∴，
又，
∴是等边三角形，
∵点，表示的刻度分别为，
∴，
∴，
∴的周长为，
故答案为：．
15．/0.5
【分析】本题考查等边三角形的性质、全等三角形的判定与性质、三角形的外角性质、含30度角的直角三角形的性质，熟练掌握等边三角形的性质，证得是解答的关键．先根据题意推出，可知，因此，所以，即可推出结论．
【详解】解：∵等边三角形，
∴，，
∵，
∴，
∴，
∴，
∴，
∴，
∵，
∴，
∴．
故答案为：．
16．相等
【分析】本题考查了翻折变换，等边三角形的判定与性质，全等三角形的判定与性质，掌握翻折变换的性质、证明三角形全等是解题的关键．由翻折知，垂直平分，则；又由翻折知，，；从而得是等边三角形，则得；再证明得，即可得两角的关系．
【详解】解：由第一次翻折知，垂直平分，
；
又由第二次翻折知，，；
，
是等边三角形，
，
，；
点的对应点为点H，
；
，
，
，
．
故答案为：相等．
17．
【分析】本题考查了等腰三角形的判定和性质，含30度角的直角三角形，掌握30度角所对应的直角边是斜边的一半，是解题的关键．
（1）连接，推出，，进而得到，得到，利用互余关系，求出即可；
（2）利用含30度的直角三角形的性质得到，证明为等腰三角形，进而得到，求出的长，证明为等腰三角形，得到即可．
【详解】解：（1）连接，

∵，
∴，
∴，
∵互相平分于点O，，
∴，
∴，
∴，
∵，
∴，
∴，
∴，
∴，
故答案为：；
（2）∵，，
∴，
∴，
∴，
∵，，
∴，，
∵，
∴，
∴，
∴；
故答案为：．
18． 3
【分析】（1）根据证明即可得出线段和之间的数量关系；
（2）以为一边在的左边作等边，作于点D，连接，根据证明即可得出，求出的最小值即可．
【详解】解：（1）∵，都是等边三角形，
∴，
∴，
∴，
∴．
故答案为：；
（2）以为一边在的左边作等边，作于点D，连接，
∵，都是等边三角形，
∴，
∴，
∴，
∴，
∴点B与点D重合时，线段取得最小值．
∵，
∴，
∴，
∴线段的最小值为3．
故答案为：3．
【点拨】此题考查了全等三角形的判定与性质，等边三角形的性质，垂线段最短，直角三角形的性质，熟练掌握全等三角形的判定与性质是解本题的关键．
19．(1)见解析
(2)或或
【分析】本题考查了等边三角形性质，等腰直角三角形的性质，全等三角形的判定，解题的关键是熟练掌握相关知识．
（1）先根据等边三角形的性质得出，，，从而得到，证得，即可得出结论；
（2）当为等腰直角三角形时，有三种情况，，，，分别讨论三种情况下的度数即可．
【详解】（1）证明：，均为等边三角形，
，，，
又，
，
，
；
（2）解：当为等腰直角三角形时，
若，则，，
；
若，则，，
，，
；
若，则，
点在线段的垂直平分线上，
，
点在线段的垂直平分线上，
垂直平分线段，
，
即或或，
故答案为：或或．
20．(1)见解析
(2)等边三角形，见解析
【分析】本题主要考查了三角形全等的判定和性质，等边三角形的判定，解题的关键是熟练掌握三角形全等的判定和性质．
（1）根据证明三角形全等即可；
（2）根据，得出，，求出，即可证明结论．
【详解】（1）证明：∵，
∴，
∵，
∴，
∵，，
∴，
在和中，
，
∴；
（2）解：是等边三角形，理由如下：
∵，
∴，
∵，
∴，，
∴，
∴，
∴，
∴是等边三角形．
21．(1)1
(2)或
【分析】本题考查了含度角的直角三角形的性质，熟练掌握度角的直角三角形的边角关系是解题的关键.
（1）根据等边三角形的性质列出方程求出t的值；
（2）分两种情况讨论: ①当为直角时, ②当为直角时，分别利用度角所对的直角边等于斜边的一半列方程求出的值.
【详解】（1）解：根据题意可得,，
∵，
∴,
∵, 为等边三角形,
∴,即,
解得：,
∴当为时, 为等边三角形；
（2）①当为直角时, ,
，即
解得；
②当为直角时, ,
∴即
解得.
∴当为 或时,为直角三角形.
22．(1)30
(2)①见解析；②
【分析】本题主要考查全等三角形的判定和性质，等边三角形的性质，折叠的性质，熟练掌握全等三角形的判定和性质及等边三角形的性质是解题的关键．
（1）由是等边三角形知，，由，知，，代入值即可；
（2）①通过折叠性质证明即可得到结论；
②在上取一点，使，连接，根据证，得，再证是等边三角形，即可得出，由，得出，即可求出的值．
【详解】（1）解：是等边三角形，
，
，
，
，
，
，
故答案为：30；
（2）①证明：把沿对折，得到，
，
，
，
又，
，
，
点在延长线上，
平分；
②如图，在上取一点，使，连接，，
是等边三角形，
，
，
，
，
，
，
是等边三角形，
，
，即，
点在同一直线上，即，
由①知，，
，，
，
，
．
23．(1)见解析
(2)①见解析；②，见解析
【分析】（1）根据，可得，再由证明，则，利用中垂线的判定定理即可证明；
（2）①设，根据可得，由于，可得，根据是的外角，则，由于，所以，从而，进而，结论得证；
②延长至，使，可得与关于成轴对称，过作于交于，即可，再利用直角三角形中30度角的性质即可得数量关系．
【详解】（1）证明：，，
，，
在的垂直平分上，，
，
在的垂直平分上，
垂直平分；
（2）①证明：设，
，
，
是的外角，
，
由（1），，
，
，
，
，
，
，即，
则，
，
，
是等边三角形；
②为最小值时，与的数量关系是，
理由：
延长至，使，
，
与关于成轴对称，过作于交于，连接，
，
，此时为最小，
由①知：，即，
即，
在中，，
，
为最小值时，与的数量关系是．
【点拨】本题考查中垂线的判定定理、等腰三角形的判定和性质、含角得的直角三角形的性质、轴对称的性质，综合题，理解题意是解决问题的关键．
24．(1)见详解
(2)见详解
(3)见详解
【分析】（1）利用定理证明，根据全等三角形的性质得到，根据等腰三角形的性质得到，等量代换证明结论；
（2）在上截取，连接，证明，根据全等三角形的性质得到，进而证明为等边三角形；
（3）延长交于，证明，得到，再证明，得到，等量代换得到答案．
【详解】（1）证明：∵平分，
，
，
，
在和中，
，
，
，
，
，
；
（2）证明：如图，在上截取，连接，
∵，
∴，
在和中，
，
∴，
∴，
∵，
∴是等边三角形，
∴，
∴，
∵，
∴为等边三角形；
（3）证明：如图3，延长、交于，
，
，
，
，
，
，
，
，
，
，
在和中，
，
，
，
即，
，
，
在和中，
，
，
，
．
【点拨】本题主要考查了全等三角形的判定和性质，等边三角形的判定和性质，平行线的性质，等腰三角形的性质，三角形内角和定理等知识点，熟练掌握全等三角形的判定和性质，等边三角形的判定和性质是解题的关键．