2024-2025学年山东省济南实验中学九上数学开学综合测试试题【含答案】

这是一份2024-2025学年山东省济南实验中学九上数学开学综合测试试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，在△ABC中，∠ACB=90°，AC=8，AB=10，DE垂直平分AC交AB于点E，则DE的长为（ ）
A．6B．5C．4D．3
2、（4分）若点A(3，y1)，B(﹣2，y2)都在直线y＝﹣x+n上，则y1与y2的大小关系是( )
A．y1＜y2B．y1＞y2
C．y1＝y2D．以上都有可能
3、（4分）把一些笔记本分给几个学生，如果每人分3本，那么余8本，如果每人分5本，则最后一个人分到的本数不足3本，则共有学生( )人．
A．4 B．5 C．6 D．5或6
4、（4分）如图，在▱ABCD中，对角线AC、BD相交于点O，下列哪个条件不能判定▱ABCD是矩形的是( )
A．AC=BDB．OA=OBC．∠ABC=90°D．AB=AD
5、（4分）如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是
A．S1＞S2B．S1=S2C．S1＜S2D．3S1=2S2
6、（4分）一元二次方程的根是（ ）
A．x  0B．x  1C．x  0, x  1D．无实根
7、（4分）如图所示，四边形OABC是矩形，△ADE是等腰直角三角形，∠ADE＝90°，点A，D在x轴的正半轴上，点C在y轴的正半轴上，点B、E在反比例函数y＝（x＞0）的图象上．△ADE的面积为，且AB＝DE，则k值为（ ）
A．18B．C．D．16
8、（4分）若点P在一次函数的图像上，则点P一定不在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，过点N（0，-1）的直线y=kx+b与图中的四边形ABCD有不少于两个交点，其中A（2，3）、B（1，1）、C（4，1）、D（4，3），则k的取值范围____________
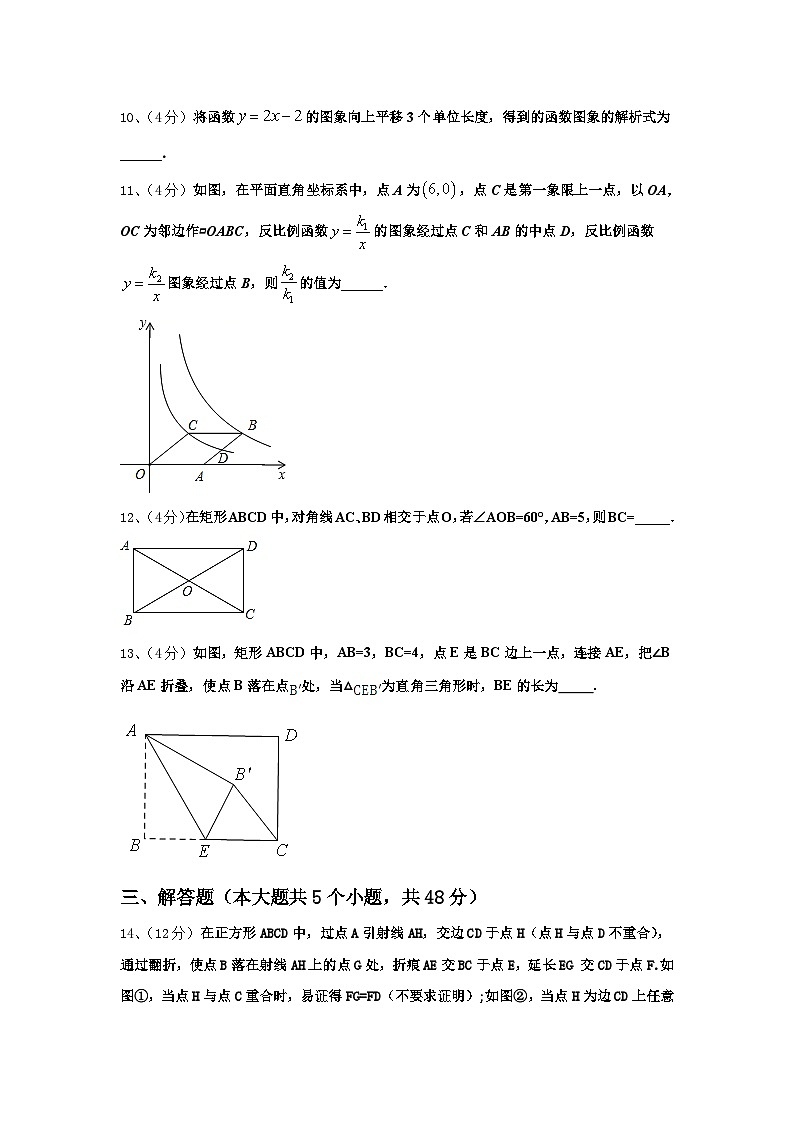
10、（4分）将函数的图象向上平移3个单位长度，得到的函数图象的解析式为______.
11、（4分）如图，在平面直角坐标系中，点A为，点C是第一象限上一点，以OA，OC为邻边作▱OABC，反比例函数的图象经过点C和AB的中点D，反比例函数图象经过点B，则的值为______．
12、（4分）在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=60°，AB=5，则BC=_____．
13、（4分）如图，矩形ABCD中，AB=3，BC=4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点处，当△为直角三角形时，BE的长为 .
三、解答题（本大题共5个小题，共48分）
14、（12分）在正方形ABCD中，过点A引射线AH，交边CD于点H（点H与点D不重合），通过翻折，使点B落在射线AH上的点G处，折痕AE交BC于点E，延长EG 交CD于点F.如图①，当点H与点C重合时，易证得FG=FD（不要求证明）;如图②，当点H为边CD上任意一点时，求证：FG=FD．
（应用）在图②中，已知AB=5，BE=3，则FD= ，△EFC的面积为 .(直接写结果)
15、（8分）骑自行车旅行越来越受到人们的喜爱，顺风车行经营的型车2017年7月份销售额为万元，今年经过改造升级后，型车每辆的销售价比去年增加元，若今年7月份与去年7月份卖出的型车数量相同，则今年7月份型车销售总额将比去年7月份销售总额增加.求今年7月份顺风车行型车每辆的销售价格．
16、（8分）先化简再求值：，其中a=-2。
17、（10分）甲、乙两人相约登山，甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示，根据图象所提供的信息解答下列问题：
(1)图中的t1= 分；
(2)若乙提速后，乙登山的速度是甲登山的速度的3倍，
①则甲登山的速度是 米/分，图中的t2= 分；
②请求出乙登山过程中，距地面的高度y(米)与登山时间x(分)之间的函数关系式．
18、（10分）当为何值时，分式的值比分式的值大2？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若关于x的不等式组的解集为﹣＜x＜﹣6，则m的值是_____．
20、（4分）如图，在△ABC中，BC的垂直平分线MN交AB于点D，CD平分∠ACB．若AD＝2，BD＝3，则AC的长为_____．
21、（4分）如图，点D是直线外一点，在上取两点A，B，连接AD，分别以点B，D为圆心，AD，AB的长为半径画弧，两弧交于点C，连接CD，BC，则四边形ABCD是平行四边形，理由是：_________________________
.
22、（4分）甲、乙两名同学的5次数学成绩情况统计结果如下表：
根据上表，甲、乙两人成绩发挥较为稳定的是______填：甲或乙
23、（4分）若关于x的一元二次方程有两个不相等的实数根，则非正整数k的值是______．
二、解答题（本大题共3个小题，共30分）
24、（8分）已知两地相距，甲、乙两人沿同一公路从 地出发到地，甲骑摩托车，乙骑自行车，如图中分别表示甲、乙离开地的距离 与时间 的函数关系的图象，结合图象解答下列问题.
（1）甲比乙晚出发___小时，乙的速度是___ ；甲的速度是___.
（2）若甲到达地后，原地休息0.5小时，从地以原来的速度和路线返回地，求甲、乙两人第二次相遇时距离地多少千米？并画出函数关系的图象.
25、（10分）如图，四边形ABCD中， BA=BC， DA=DC，我们把这种两组邻边分别相等的四边形叫做“筝形”， 其对角线AC、BD交于点M，请你猜想关于筝形的对角线的一条性质，并加以证明.
猜想：
证明：
26、（12分）化简：；
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
试题分析：已知，在△ABC中，∠ACB=90°，AC=8，AB=10，根据勾股定理可得BC=6，又因DE垂直平分AC，∠ACB=90°，可得DE为△ABC的中位线，根据三角形的中位线定理可得DE=BC=3，故答案选D.
考点：勾股定理；三角形的中位线定理.
2、A
【解析】
结合题意点A(3，y1)，B(﹣1，y1)都在直线y＝﹣x+n上，利用一次函数的增减性即可解决问题.
【详解】
∵直线y＝﹣x+n，
﹣＜0，
∴y随x的增大而减小，
∵3＞﹣1，
∴y1＜y1．
故选：A．
本题考查一次函数图象上的点的特征，解题的关键是学会利用一次函数的增减性解决问题，属于中考常考题型．
3、C
【解析】
根据每人分3本，那么余8本，如果前面的每个学生分1本，那么最后一人就分不到3本，得出3x+8≥1（x-1），且1（x-1）+3＞3x+8，分别求出即可．
【详解】
假设共有学生x人，根据题意得出：
1（x-1）+3＞3x+8≥1（x-1），
解得：1＜x≤6.1．
故选：C．
本题考查了不等式组的应用，解题关键是根据题意找出不等关系得出不等式组．
4、D
【解析】
根据平行四边形的性质，矩形的判定方法即可一一判断即可．
【详解】
解：∵四边形ABCD是平行四边形，
∵AC=BD，
∴ABCD是矩形，故A正确；
∵四边形ABCD是平行四边形，
∴AO=OC，BO=OD，
∵OA=OB，
∴AC=BD，
∴ABCD是矩形，故B正确；
∵四边形ABCD是平行四边形，
∵∠ABC=90°，
∴ABCD是矩形，故C正确；
∵四边形ABCD 是平行四边形，
∵AB=AD，
∴ABCD是菱形，故D错误．
故选：D．
本题考查了矩形的判定，平行四边形的性质，熟练掌握矩形的判定定理是解题的关键．
5、B
【解析】
由于矩形ABCD的面积等于2个△ABC的面积，而△ABC的面积又等于矩形AEFC的一半，所以可得两个矩形的面积关系．
【详解】
∵矩形ABCD的面积S=2S△ABC， S△ABC=S矩形AEFC，
∴S1=S2
故选B
6、C
【解析】
先移项得到，再把方程左边分解因式得到，原方程转化为或，然后解两个一元一次方程即可.
【详解】
，
，
或，
，.
故选：.
本题考查了解一元二次方程-因式分解法：先把方程右边变形为0，再把方程左边分解为两个一次式的乘积，这样原方程转化为两个一元一次方程，然后解一次方程即可得到一元二次方程的解.
7、B
【解析】
设B（m，5），则E（m+3，3），因为B、E在y＝上，则有5m＝3m+9＝k，由此即可解决问题；
【详解】
解：∵△ADE是等腰直角三角形，面积为，
∴AD＝DE＝3，
∵AB＝DE，
∴AB＝5，设B（m，5），则E（m+3，3），
∵B、E在y＝上，
则有5m＝3m+9＝k
∴m＝，
∴k＝5m＝.
故选B．
本题考查反比例函数系数k的几何意义，等腰直角三角形的性质等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．
8、C
【解析】
根据一次函数的性质进行判定即可.
【详解】
一次函数y=-x+4中k=-1<0，b>0，
所以一次函数y=-x+4的图象经过二、一、四象限，
又点P在一次函数y=-x+4的图象上，
所以点P一定不在第三象限，
故选C.
本题考查了一次函数的图象和性质，熟练掌握是解题的关键.
y=kx+b：当 k>0，b>0时，函数的图象经过一，二，三象限；当 k>0，b<0时，函数的图象经过一，三，四象限；当 k<0，b>0时，函数的图象经过一，二，四象限；当 k<0，b<0时，函数的图象经过二，三，四象限.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、＜k≤2．
【解析】
直线y=kx+b过点N（0，-2），则b=-2，y=kx-2．当直线y=kx-2的图象过A点时，求得k的值；当直线y=kx-2的图象过B点时，求得k的值；当直线y=kx-2的图象过C点时，求得k的值，最后判断k的取值范围．
【详解】
∵直线y=kx+b过点N（0，-2），
∴b=-2，
∴y=kx-2．
当直线y=kx-2的图象过A点（2，3）时，
2k-2=3，k=2；
当直线y=kx-2的图象过B点（2，2）时，
k-2=2，k=2；
当直线y=kx-2的图象过C点（4，2）时，
4k-2=2，k=，
∴k的取值范围是＜k≤2．
故答案为＜k≤2．
本题主要考查了运用待定系数法求一次函数解析式，解题时注意：求正比例函数y=kx，只要一对x，y的值；而求一次函数y=kx+b，则需要两组x，y的值．
10、
【解析】
根据一次函数的图像平移的特点即可求解.
【详解】
函数的图象向上平移3个单位长度，得到的函数图象的解析式为+3，
∴函数为
此题主要考查一次函数的性质，解题的关键是熟知一次函数平移的特点.
11、
【解析】
过C作CE⊥x轴于E，过D作DF⊥x轴于F，易得△COE∽△DAF，设C（a，b），则利用相似三角形的性质可得C（4，b），B（10，b），进而得到.
【详解】
如图，过C作CE⊥x轴于E，过D作DF⊥x轴于F，则∠OEC=∠AFD=90°，
又，
，
∽，
又是AB的中点，，
，
设，则，，
，，
，
反比例函数的图象经过点C和AB的中点D，
，
解得，
，
又，
，
，
故答案为．
本题考查了反比例函数图象上点的坐标特征以及平行四边形的性质，解题的关键是掌握：反比例函数图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．
12、5；
【解析】
根据矩形性质得出AC=2AO，BD=2BO，AC=BD，推出AO=OB，得出等边三角形AOB，利用勾股定理即可得出答案．
【详解】
∵四边形ABCD是矩形，
∴AC=BD，AC=2AO，BD=2BO，∠ABC=90°，
∴AO=OB，
∵∠AOB=60°，
∴△AOB是等边三角形，
∴AO=AB=5，
∴AC=2 AO=10，
在Rt△ABC中，由勾股定理得，
BC=.
故答案为：5.
本题考查了矩形的性质及勾股定理.根据矩形的性质及∠AOB=60°得出△AOB是等边三角形是解题的关键.
13、1或．
【解析】
当△CEB′为直角三角形时，有两种情况：
①当点B′落在矩形内部时，如答图1所示．
连结AC，先利用勾股定理计算出AC=5，根据折叠的性质得∠AB′E=∠B=90°，而当△CEB′为直角三角形时，只能得到∠EB′C=90°，所以点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，则EB=EB′，AB=AB′=1，可计算出CB′=2，设BE=x，则EB′=x，CE=4-x，然后在Rt△CEB′中运用勾股定理可计算出x．
②当点B′落在AD边上时，如答图2所示．此时ABEB′为正方形．
【详解】
当△CEB′为直角三角形时，有两种情况：
①当点B′落在矩形内部时，如答图1所示．
连结AC，
在Rt△ABC中，AB=1，BC=4，
∴AC==5，
∵∠B沿AE折叠，使点B落在点B′处，
∴∠AB′E=∠B=90°，
当△CEB′为直角三角形时，只能得到∠EB′C=90°，
∴点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，
∴EB=EB′，AB=AB′=1，
∴CB′=5-1=2，
设BE=x，则EB′=x，CE=4-x，
在Rt△CEB′中，
∵EB′2+CB′2=CE2，
∴x2+22=（4-x）2，解得，
∴BE=；
②当点B′落在AD边上时，如答图2所示．
此时ABEB′为正方形，∴BE=AB=1．
综上所述，BE的长为或1．
故答案为：或1．
三、解答题（本大题共5个小题，共48分）
14、（1）证明见解析；（2）应用：；
【解析】
试题分析：由折叠的性质可得AB=AG=AD，∠AGF=∠AGE=∠B=∠D=90°,再结合AF为△AGF和△ADF的公共边，从而证明△AGF≌△ADF，从而得出结论．
[应用]设FG=x，则FC=5-x，FE=3+x，在Rt△ECF中利用勾股定理可求出x的值，进而可得出答案．
试题解析：（1）由翻折得AB=AG,∠AGE=∠ABE=90°
∴∠AGF=90°
由正方形ABCD得 AB=AD
∴AG=AD
在Rt△AGF和Rt△ADF中，

∴Rt△AGF ≌ Rt△ADF
∴FG=FD
（2）[应用]设FG=x，则FC=5-x，FE=3+x，
在Rt△ECF中，EF2=FC2+EC2，即（3+x）2=（5-x）2+22，
解得x=.
即FG的长为．
由（1）得：FD=FG=，FC=5-=，BC=AB=5，BE=3
∴EC=5-3=2
∴ΔEFC的面积=
15、2000
【解析】
设去年A型车每辆x元，那么今年每辆（x＋400）元，列出方程即可解决问题．
【详解】
解：设去年A型车每辆x元，那么今年每辆（x＋400）元，
根据题意得
解得x＝1600，
经检验，x＝1600是方程的解．
答：今年A型车每辆2000元．
本题考查了分式方程的应用，解题的关键是设未知数列出方程解决问题，注意分式方程必须检验.
16、,3
【解析】
可先对括号内，进行化简约分，对括号外除法化乘法，然后对括号内同分母分式加法进行计算，最后进行约分即可得到化简之后的结果，将a=-2代入化简之后的结果进行计算.
【详解】
原式=



当a=-2，原式=3
本题考查分式的化简求值，对于分式的化简在运算过程中要根据运算法则注意运算顺序，在化简过程中可先分别对分母分子因式分解，再进行约分计算.
17、 (1)2；(2)①10，20；②．
【解析】
（1）根据高度=速度×时间即可算出t1的值；
（2）①根据“高度=速度×时间”列式计算即可；②运用待定系数法求出线段OA与线段AB的解析式即可．
【详解】
(1)t1=30÷15=2
故答案为：2；
(2)①甲登山上升的速度是：(300-100)÷20=10(米/分钟)，
故答案为：10，20；t2=(300-100)÷10=20，
②当0≤x≤2时，直线过原点，且经过点(2，30)，
∴y=15x，
当2＜x≤11时，设y=kx+b，直线过点(2，30)，(11，300)
得，
y与x的数解析式也可以合起来表示为：
．
本题考查了一次函数的应用以及解一元一次方程，解题的关键是：（1）根据数量关系列式计算；（2）根据高度=初始高度+速度×时间找出y关于x的函数关系式．
18、当时，分式的值比分式的值大2.
【解析】
根据题意列出方程，求出方程的解即可得到x的值．
【详解】
解：根据题意得：
方程两边同乘以约去分母，得：
化简整理，得：
解得
经检验：是原方程的根，
所以，原方程的根是：
所以，当时，分式的值比分式的值大2.
此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1
【解析】
先解不等式组得出其解集为，结合可得关于的方程，解之可得答案．
【详解】
解不等式，得：，
解不等式，得：，
∵不等式组的解集为，
∴，
解得，
故答案为：1．
本题考查了解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
20、
【解析】
作AM⊥BC于E，由角平分线的性质得出，设AC＝2x，则BC＝3x，由线段垂直平分线得出MN⊥BC，BN＝CN＝x，得出MN∥AE，得出，NE＝x，BE＝BN＋EN＝x，CE＝CN−EN＝x，再由勾股定理得出方程，解方程即可得出结果．
【详解】
解：作AM⊥BC于E，如图所示：
∵CD平分∠ACB，
∴，
设AC＝2x，则BC＝3x，
∵MN是BC的垂直平分线，
∴MN⊥BC，BN＝CN＝x，
∴MN∥AE，
∴，
∴NE＝x，
∴BE＝BN＋EN＝x，CE＝CN−EN＝x，
由勾股定理得：AE2＝AB2−BE2＝AC2−CE2，
即52−（x）2＝（2x）2−（x）2，
解得：x＝，
∴AC＝2x＝；
故答案为．
本题考查了线段垂直平分线的性质、角平分线的性质、平行线分线段成比例定理、勾股定理等知识；熟练掌握线段垂直平分线的性质和角平分线的性质，由勾股定理得出方程是解题的关键．
21、两组对边分别相等的四边形是平行四边形.
【解析】
先根据分别以点B，D为圆心，AD，AB的长为半径画弧，两弧交于点C，连接CD，BC，得出AB=DC，AD=BC，根据“两组对边分别相等的四边形是平行四边形”可判断四边形ABCD是平行四边形．
【详解】
解：根据尺规作图的作法可得，AB=DC，AD=BC，
∴四边形ABCD是平行四边形（两组对边分别相等的四边形是平行四边形）
故答案为两组对边分别相等的四边形是平行四边形．
本题主要考查了平行四边形的判定，解题时注意：两组对边分别相等的四边形是平行四边形．符号语言为：∵AB=DC，AD=BC，∴四边形ABCD是平行四边形．
22、甲
【解析】
根据方差的定义，方差越小数据越稳定．
【详解】
∵S甲2=4，S乙2=16，
∴S甲2=4＜S乙2=16，
∴成绩稳定的是甲，
故答案为：甲．
本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
23、-1
【解析】
根据判别式的意义及一元二次方程的定义得到，且，然后解不等式即可求得k的范围，从而得出答案．
【详解】
解：根据题意知，且，
解得：且，
则非正整数k的值是，
故答案为：．
本题考查了一元二次方程的根的判别式：当，方程有两个不相等的实数根；当，方程有两个相等的实数根；当，方程没有实数根．
二、解答题（本大题共3个小题，共30分）
24、（1）1，15，60；（2）42，画图见解析.
【解析】
（1）根据函数图象可以解答本题；
（2）根据题意画出函数图像，可以求得所在直线函数解析式和所在直线的解析式，从而可以解答本题．
【详解】
解：（1）由图象可得，甲比乙晚出发1小时，乙的速度是：30÷2＝15km/h，甲的速度是：60÷1=60km/h，
故答案为1，15，60；
（2）画图象如图.
设甲在返回时对应的所在直线函数解析式为：，
由题意可知，M(2.5，60)，N（3.5，0），
将点M、N代入可得： ，解得
甲在返回时对应的函数解析式为：
设所在直线的解析式为：，
∴，解得，
所在直线的解析式为：，
联立，
消去得
答：甲、乙两人第二次相遇时距离地42千米．
本题考查一次函数的应用，解题的关键是明确题意，正确识图并找出所求问题需要的条件．
25、筝形有一条对角线平分一组对角，即BD平分∠ABC且BD平分∠ADC；证明见解析
【解析】
利用SSS定理证明△ABD≌△CBD，可得∠ABD=∠CBD，∠ADB=∠CDB，从而可写出关于筝形的对角线的一条性质，筝形有一条对角线平分一组对角.
【详解】
解：筝形有一条对角线平分一组对角，即BD平分∠ABC且BD平分∠ADC
证明：∵在△ABD和△CBD中
BA=BC，DA=DC，BD=BD
∴△ABD≌△CBD(SSS)
∴∠ABD=∠CBD，∠ADB=∠CDB
即BD平分∠ABC，且BD平分∠ADC.
本题考查全等三角形的判定及性质，掌握SSS定理及全等三角形对应角相等是本题的解题关键.
26、．
【解析】
先把二次根式化为最简二次根式，然后合并后进行二次根式的除法运算．
【详解】
解：原式
．
本题考查了二次根式的混合运算，解题关键在于结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径．
题号
一
二
三
四
五
总分
得分
平均分
方差
标准差
甲
80
4
2
乙
80
16
4